
题目列表(包括答案和解析)
(15) (本小题满分13分)
△ABC中,角A、B、C的对边分别为a,b,c.
(Ⅰ)若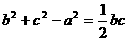 ,求cosA的值;
,求cosA的值;
(Ⅱ)若A∈[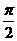 ,
,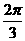 ],求
],求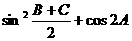 的取值范围.
的取值范围.
(16)(本小题满分13分)
一个袋子里装有大小相同,且标有数字1~5的若干个小球,其中标有数字1的小球有1个,标有数字2的小球有2个,…,标有数字5的小球有5个.
(Ⅰ) 从中任意取出3个小球,求取出的小球都标有偶数数字的概率;
(Ⅱ)从中任意取出2个小球,求小球上所标数字之和为6的概率;
(Ⅲ) 设任意取出的1个小球上所标数字为ξ,求Eξ.
(17) (本小题满分13分)
已知:四棱锥P-ABCD的底面ABCD是边长为1的正方形,PD⊥底面ABCD,且PD=1.
(Ⅰ) 求证:BC∥平面PAD;
(Ⅱ)若E、F分别为PB、AD的中点,求证:EF⊥平面PBC;
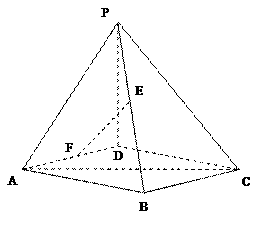 (Ⅲ)求二面角B-PA-C的余弦值.
(Ⅲ)求二面角B-PA-C的余弦值.
(18)(本小题满分13分)
已知函数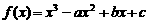 .
.
(Ⅰ) 若函数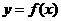 的图象上存在点P,使P点处的切线与x轴平行,求实数a,b的关系式;
的图象上存在点P,使P点处的切线与x轴平行,求实数a,b的关系式;
(Ⅱ) 若函数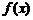 在
在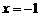 和
和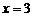 时取得极值,且其图象与
时取得极值,且其图象与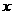 轴有且只有3个交点,求实数
轴有且只有3个交点,求实数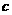 的取值范围.
的取值范围.
(19)(本小题满分14分)
已知O为坐标原点,点E、F的坐标分别为(-1,0)、(1,0),动点A、M、N满足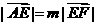 (
(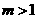 ),
),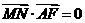 ,
,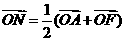 ,
,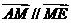 .
.
(Ⅰ)求点M的轨迹W的方程;
(Ⅱ)点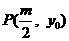 在轨迹W上,直线PF交轨迹W于点Q,且
在轨迹W上,直线PF交轨迹W于点Q,且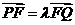 ,若
,若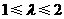 ,求实数
,求实数 的范围.
的范围.
(20)(本小题满分14分)
在下列由正数排成的数表中,每行上的数从左到右都成等比数列,并且所有公比都等于q,每列上的数从上到下都成等差数列.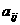 表示位于第
表示位于第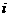 行第
行第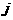 列的数,其中
列的数,其中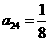 ,
,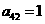 ,
,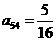 .
.
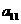 |
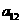 |
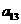 |
 |
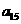 |
… |
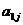 |
… |
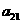 |
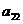 |
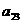 |
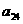 |
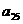 |
… |
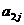 |
… |
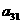 |
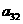 |
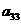 |
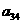 |
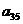 |
… |
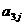 |
… |
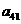 |
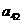 |
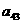 |
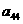 |
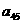 |
… |
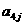 |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
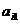 |
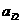 |
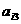 |
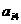 |
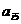 |
… |
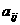 |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
(Ⅰ) 求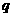 的值;
的值;
(Ⅱ) 求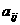 的计算公式;
的计算公式;
(Ⅲ)设数列{bn}满足bn=ann,{bn}的前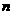 项和为
项和为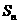 ,试比较
,试比较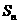 与Tn=
与Tn=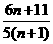 ( n∈N*) 的大小,并说明理由.
( n∈N*) 的大小,并说明理由.
朝阳区高三第二次统一考试
横线上.
(9) 已知向量a= (4,3),b = (x,-4),且a⊥b,则x = .
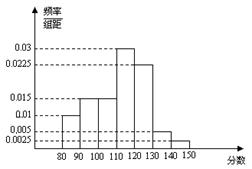 (10) 若x,y满足约束条件
(10) 若x,y满足约束条件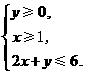 则z=x+y的最大值为 .
则z=x+y的最大值为 .
(11) 高三某班50名学生参加某次数学
模拟考试,所得的成绩(成绩均为整
数)整理后画出的频率分布直方图如
右图,则该班得120分以上的同学共
有 人.
(12) 已知曲线C的参数方程是:
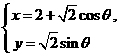 (θ为参数),则曲线C的普通方程是
;曲线C被直线x-
(θ为参数),则曲线C的普通方程是
;曲线C被直线x-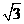 y=0所截得的弦长是
.
y=0所截得的弦长是
.
(13) 设常数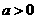 ,
,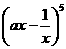 展开式中
展开式中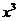 的系数为-
的系数为-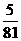 ,则a= ,
,则a= ,
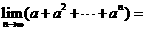 ___ __.
___ __.
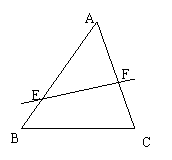
(14) 在△ABC中,E、F分别为AB、AC上的点,若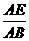 =m,
=m,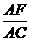 =n,则
=n,则
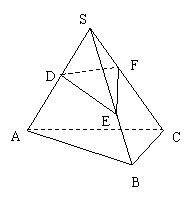
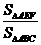 = mn. 拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若
= mn. 拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若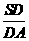 = m,
= m,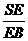 =n,
=n,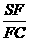 = p,则
= p,则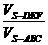 = .
= .
4个选项中,只有一项是符合题目要求的.
(1) 已知复数z1=2+mi (m∈R),z2=4-3i,若z1·z2为实数,则m的值为 ( )
A. 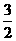 B. -
B. -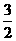 C. -
C. -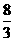 D.
D. 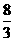
(2) 不等式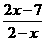 >-1的解集是
( )
>-1的解集是
( )
A. {x| x >5或 x<2} B. {x| 2< x<5}
C. {x| x >5或 x<-2} D.{x| -2< x<5}
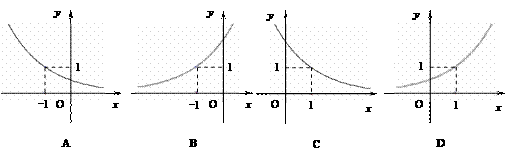
(3) 与函数y=2x-1的图象关于y轴对称的函数图象是 ( )
(4) 已知直线a和平面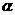 、
、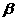 ,
,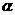 ∩
∩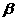 =l,a
=l,a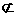
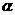 ,a
,a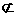
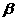 ,a在
,a在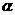 、
、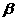 内的射影分别为直线b和c,则b、c的位置关系是
( )
内的射影分别为直线b和c,则b、c的位置关系是
( )
A.相交或平行 B.相交或异面 C.平行或异面 D.相交,平行或异面
(5) 把函数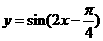 的图象向右平移
的图象向右平移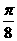 个单位,所得的图象对应的函数( )
个单位,所得的图象对应的函数( )
A. 是奇函数 B. 是偶函数 C.既是奇函数又是偶函数 D. 是非奇非偶函数
(6) 某电视台连续播放5个广告,其中3个不同的商业广告和2个不同的奥运宣传广告,要求最后播放的必须是奥运宣传广告,且2个奥运宣传广告不能连续播放,则不同的播放方式有 ( )
A.120种 B.48种 C.36种 D.18种
(7) 对函数f(x)=ax2+bx+c (a≠0,b、c∈R)作x=h(t)的代换,使得代换前后函数的值域总不改变的代换是 ( )
A. h(t)=10t B. h(t)=t2 C. h(t)=sint D. h(t)=log2t
(8) 已知圆F的方程是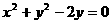 ,抛物线的顶点在原点,焦点是圆心F,过F引倾斜角为
,抛物线的顶点在原点,焦点是圆心F,过F引倾斜角为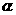 的直线l,l与抛物线和圆依次交于A、B、C、D四点(在直线l上,这四个点从左至右依次为A、B、C、D),若
的直线l,l与抛物线和圆依次交于A、B、C、D四点(在直线l上,这四个点从左至右依次为A、B、C、D),若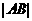 ,
,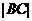 ,
, 成等差数列,则
成等差数列,则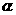 的值为
(
)
的值为
(
)
A.±arctan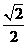 B.
B.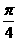
C.arctan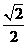 D.arctan
D.arctan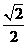 或π- arctan
或π- arctan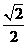
朝阳区高三第二次统一考试数学试卷(理科)
第II卷(非选择题 共110分)
|
二 题 |
9 |
10 |
11 |
12 |
13 |
14 |
二题 总分 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
||||||||||||||||||||
|
三 题 |
15 |
16 |
17 |
18 |
19 |
20 |
||||||||||||||||
|
Ⅰ |
Ⅱ |
Ⅰ |
Ⅱ |
Ⅲ |
Ⅰ |
Ⅱ |
Ⅲ |
Ⅰ |
Ⅱ |
Ⅰ |
Ⅱ |
Ⅰ |
Ⅱ |
Ⅲ |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
三题 总分 |
|
二卷 总分 |
|
|||||||||||||||||||
40、若定义在区间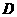 上的函数
上的函数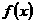 对
对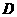 上的任意
上的任意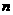 个值
个值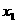 ,
,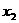 ,…,
,…,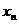 ,总满足
,总满足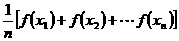 ≤
≤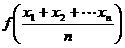 ,则称
,则称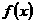 为
为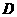 上的凸函数.已知函数
上的凸函数.已知函数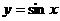 在区间
在区间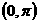 上是“凸函数”,则在△
上是“凸函数”,则在△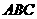 中,
中,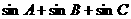 的最大值是____________________.
的最大值是____________________.
答案:1 C 、 2 C 、3 A 、4 B 、5 D 、6 B 、7 D 、8 A 、9 C 、10 C 、11 B 、12 C 、13 C、14 C 、15 B 、 16 B 、17 A 、18 D 、19 A 、20 B 、
21 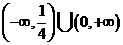 、 22
、 22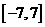 、 23
、 23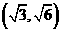 、 24 10、 25 2、 26
、 24 10、 25 2、 26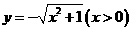 27
27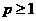 、 28
、 28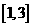 、 29
、 29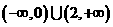 、 30
、 30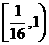 、 31
、 31 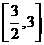 32
32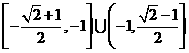 、 33 2、 34
、 33 2、 34 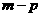 、35
、35 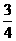 或
或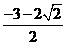 、 36
4、
37
、 36
4、
37 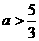 或
或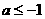 、 38
、 38 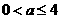 或
或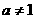 、 39
、 39 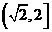 、40
、40 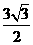 。
。
欢迎访问
39、若曲线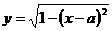 与
与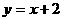 有且只有一个公共点
有且只有一个公共点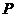 ,
, 为坐标原点,则
为坐标原点,则
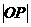 的取值范围是________________________.
的取值范围是________________________.
38、若函数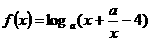 (
(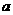 >0且
>0且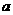 ≠1)的值域为
≠1)的值域为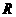 ,则实数
,则实数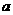 的取值范围是________________.
的取值范围是________________.
37、已知函数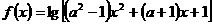 的定义域为
的定义域为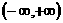 ,则实数
,则实数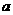 的取值范围是________________________.
的取值范围是________________________.
36、对于任意实数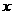 、
、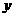 ,定义运算
,定义运算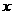 *
*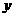 为:
为: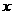 *
*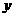 =
=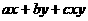 ,其中
,其中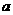 、
、 、
、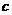 为常数,等式右边的运算是通常的加法和乘法运算,现已知1*2=3,2*3=4,并且有一个非零常数
为常数,等式右边的运算是通常的加法和乘法运算,现已知1*2=3,2*3=4,并且有一个非零常数 ,使得对于任意实数
,使得对于任意实数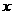 ,都有
,都有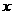 *
* =
=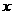 ,则
,则 =___________________________________.
=___________________________________.
35、已知函数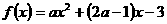 (
(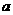 ≠0)在区间
≠0)在区间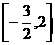 上的最大值为1,则实数
上的最大值为1,则实数
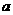 的值是____________________.
的值是____________________.
34、已知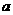 >1,
>1, >
>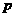 >0,若方程
>0,若方程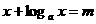 的解是
的解是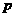 ,则方程
,则方程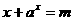 的解是____________________.
的解是____________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com