17.事件A恰好发生k次的概率为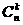P^k(1-P)^n-k，事件A发生偶数次的概率为　

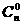? P₀(1-P)ⁿ+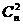P₂(1-P)^n-2+ ·P(1-P)^n-4+…+［(1-P)+P］ⁿ

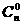= (1-P)ⁿP⁰+ 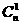(1-P)^n-1P+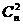·(1-P)^n-2·P²+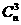(1-P)^n-3P³+…　 ①　

［(1-P)+(-P)］ⁿ=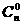 (1-P)ⁿ(-P)ⁿ+ 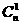(1-P)^n-1·(-P)+ 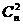(1-P)^n-2(-P)²+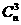(1-P)^n-3(-P)³+…　 ②　

①+②得　［(1-P)+P］ⁿ+［(1-P)+(-P)］ⁿ=2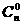［(1-P)ⁿP⁰+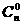(1-P)^n-2·P²+…］.　

所以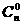(1-P)ⁿ·P⁰+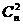(1-P)^n-2·P²+…=［1+(1-2P)ⁿ］.　

故事件A发生偶次的概率为.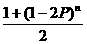

16.(1)先对A中7个元素分为两组有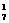C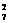+C+C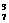=63种，再将每次分组分别对应0，1有A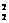种，故共有63×2=126个这样的函数.

(2)从B中0，1分别在A中选元素入手，由(1)先有C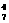种，第二步由0选只有1种，故

共有C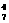=35种.

15.解析一:由于只考虑抽出的人数而不考虑具体人选，并且每班至少一人，因此只需考虑除去每班1人外的剩余3个名额的抽取方法.而三个名额的分组形式为“1,1,1”或“2,1,0”或“3,0,0”.因此可分三类：第一类：若再从7个班中抽出3个班每班1人，有C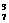种方法.

第二类:若再从7个班中抽出2个班每班分别有2人或1人，有A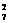种方法.

第三类:若再从7个班中抽出1个班，从中抽出3人，有C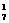种方法.

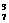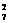根据加法原理共有:N=C+P+C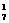=84种方法.

解析二:［隔板法］本题相当于将10个名额分成7组(每组至少1个名额)对应7个班.因此，可作如下考虑：

10人形成9个相邻空位，欲分成7部分，需用6个“隔板”任意插入9个空位中，不同的插入方法共有：C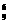=84(种).

点评：本例由于只考虑人数，而不考虑具体人选.即元素之间不可区分，故才可用上述两种方法.

14. 0.91 因为各元件能否正常工作是相互独立的，所以所求概率P=0.99⁹≈0.91.

13.　 ∵.

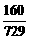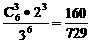12.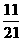 从中取一奇数、一偶数组成的分数既约，又11、13互质，∴概率为=.　

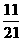11.70　 从7个方格选出3个方格，有C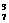，3个方格的数字重排，但没有一个数字与先前数字相同有2种，故共有C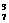·2＝70(种).

10.D　 所有4点的组合数为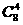，共面的情况：6个面、6个对角面；三棱锥的4个顶点不共面，故所求概率为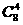-12.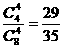

9.C?8个学生的生日占用8天，每个学生的生日都有365种可能．

8.C ∵×+×=,∴选C.