
题目列表(包括答案和解析)
2.等差数列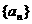 中,
中,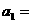 4,
4,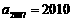 ,则公差
,则公差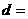 .
.
分,否则一律得零分.
1.设集合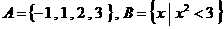 ,则A∩B =___________________.
,则A∩B =___________________.
22.(本题满分14分)
已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且
满足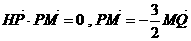 .
.
⑴ 当点P在y轴上移动时,求点M的轨迹G;
⑵ 过点T(-1,0)作直线l与轨迹G交于A、B两点,若在x轴上存在一点E(x0,0),
使得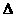 ABE是等边三角形,求x0的值.
ABE是等边三角形,求x0的值.
21.(本题满分12分)
已知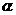 为锐角,且
为锐角,且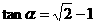 ,函数
,函数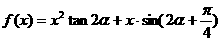 ,数列{an}
,数列{an}
的首项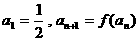 .
.
⑴ 求函数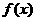 的表达式;
的表达式;
⑵ 求证: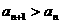 ;
;
⑶ 求证: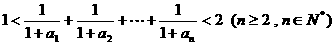 .
.
20、(本题满分12分)
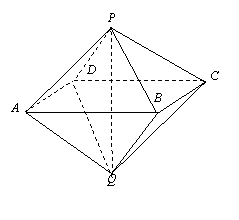 如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.
如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.
⑴ 证明PQ⊥平面ABCD;
⑵ 求异面直线AQ与PB所成的角;
⑶ 求点P到平面QAD的距离.
19、(本题满分12分)
已知函数f(x)= -x2+ax+1-lnx .
⑴ 若f(x)是在(0,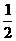 )上的减函数,求a的取值范围;
)上的减函数,求a的取值范围;
⑵ 函数f(x)是否既有极大值又有极小值,若不存在,请说明理由;若存在,求a的取
值范围.
18、(本小题满分12分)
袋中一共装有4个黑球和3个白球,现有甲、乙两人从袋中轮流摸球,每次取一个.甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用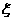 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
⑴ 求随机变量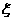 的概率分布; ⑵ 求甲取到白球的概率.
的概率分布; ⑵ 求甲取到白球的概率.
17、(本小题满分12分)
A、B、C为△ABC的三内角,且其对边分别为a、b、c.若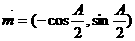 ,
,
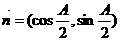 ,且
,且 ·
·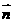 =.
=.
⑴ 求角A的大小;
⑵ 若a=2,三角形面积S=,求b+c的值.
16、定义点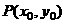 到直线
到直线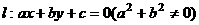 的有向距离为:
的有向距离为:
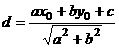 .已知点
.已知点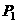 、
、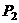 到直线
到直线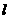 的有向距离分别是
的有向距离分别是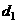 、
、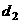 ,有以下命题:
,有以下命题:
①若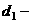
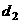 =0,则直线
=0,则直线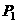
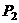 与直线
与直线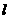 平行;②若
平行;②若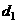 +
+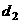 =0,则直线
=0,则直线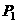
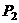 与直线
与直线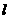 平行;
平行;
③若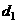 +
+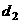 =0,则直线
=0,则直线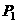
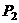 与直线
与直线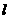 垂直;④若
垂直;④若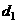
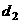 <0,则直线
<0,则直线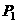
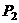 与直线
与直线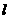 相交。
相交。
以上结论正确的是 .(要求填上正确结论的序号)
15、已知: 命题p:不等式|x-m|+|x-1|>1的解集为R,
命题q:f(x)=log(3+m)x是(0,+∞)上的增函数.
若“p且q”是假命题,“p或q”是真命题,则实数m的取值范围是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com