
题目列表(包括答案和解析)
21. (本小题满分16分,第1小问满分5分,第2小问满分5分,第3小问满分6分)
已知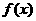 在
在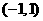 上有定义,
上有定义,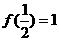 ,且满足
,且满足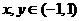 有
有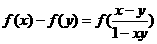 。对数列
。对数列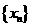 有
有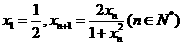
(1)
证明: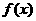 在
在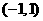 上为奇函数。
(2)求
上为奇函数。
(2)求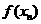 的表达式。
的表达式。
(3)是否存在自然数 ,使得对于任意
,使得对于任意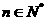 且
且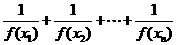 <
<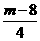 成立?若存在,求出
成立?若存在,求出 的最小值。
的最小值。
20.(本小题满分15分,第1小问满分6分,第2小问满分9分)
已知椭圆C的方程是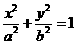 (a>b>0),斜率为1的直线
(a>b>0),斜率为1的直线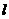 与椭圆C交于
与椭圆C交于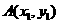 ,
,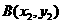 两点。
两点。
(Ⅰ)若椭圆的离心率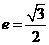 ,直线
,直线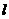 过点
过点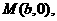 且
且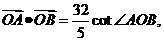 求椭圆的方程;
求椭圆的方程;
(Ⅱ)直线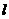 过椭圆的右焦点F,设向量
过椭圆的右焦点F,设向量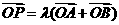 (λ>0),若点P在椭圆C上,求λ的取值范围。
(λ>0),若点P在椭圆C上,求λ的取值范围。
19.(本小题满分15分,第1小问满分5分,第2小问满分5分,第3小问满分5分)
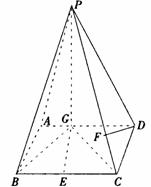 已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG=
已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG=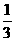 GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P-BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P-BCG的体积为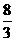 .
.
(1)求异面直线GE与PC所成的角;
(2)求点D到平面PBG的距离;
(3)若F点是棱PC上一点,且DF⊥GC,求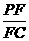 的值.
的值.
18.(本小题满分12分,第1小问满分6分,第2小问满分6分)
在某次空战中,甲机先向乙机开火,击落乙机的概率时0.2;若乙机未被击落,就进行还击,击落甲机的概率时0.3;若甲机未被击落,则再进攻乙机,击落乙机的概率时0.4,求在这个三个回合中:
(1)甲机被击落的概率;
(2)乙机被击落的概率。
17.(本小题满分12分,第1小问满分5分,第2小问满分7分)
设函数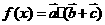 ,其中向量
,其中向量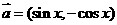 ,
,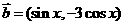 ,
,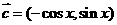 ,
,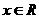 。
。
(Ⅰ)、求函数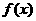 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)、将函数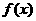 的图像按向量
的图像按向量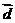 平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的
平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的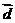 。
。
16.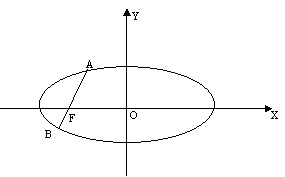 如图,AB是过椭圆
如图,AB是过椭圆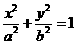 (a>b>0)的左焦点F的一条动弦,AB的斜率
(a>b>0)的左焦点F的一条动弦,AB的斜率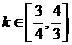 并且
并且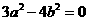 ,记
,记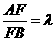 ,则
,则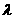 的取值范围为
的取值范围为
15.数列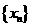 满足
满足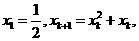 则
则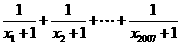 的整数部分是
的整数部分是
14.在正四面体的一个顶点处,有一只蚂蚁每一次都以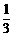 的概率从一个顶点爬到另一个顶点,那么它爬行了4次又回到起点的概率是
的概率从一个顶点爬到另一个顶点,那么它爬行了4次又回到起点的概率是
13.在坐标平面内,不等式组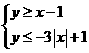 所表示的平面区域的面积为
所表示的平面区域的面积为
12.已知函数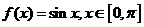 ,则
,则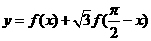 的值域为
的值域为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com