
题目列表(包括答案和解析)
19.(本小题满分14分)
|
 都在直线l:
都在直线l: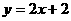 上,P1为直线l与x轴的交点,数列
上,P1为直线l与x轴的交点,数列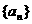 成等差数列,公差为1。
成等差数列,公差为1。
(Ⅰ)求数列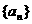 ,
,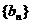 的通项公式;
的通项公式;
(Ⅱ)若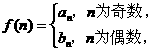 问是否存在
问是否存在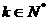 ,使得
,使得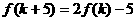 成立?若存在,求出k的值,若不存在,说明理由。
成立?若存在,求出k的值,若不存在,说明理由。
(Ⅲ)求证: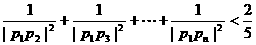

18.(本小题满分13分)
已知函数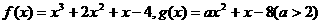
(Ⅰ)求函数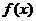 极值;
极值;
(Ⅱ)若对任意的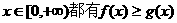 ,求实数a的取值范围.
,求实数a的取值范围.
17.(本小题满分14分)
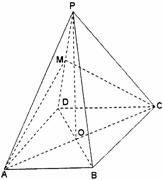 如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB//CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点。
如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB//CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点。
(Ⅰ)证明:PD⊥AC;
(Ⅱ)求二面角P-AB-C的大小;
(Ⅲ)若DM : MP=k,则当k为何值时
直线PB⊥//平面ACM?
|
16.(本小题满分13分)
有红色和黑色两个盒子,红色盒中有6张卡片,其中一张标有数字0,两张标有数字1,三张标有数字2;黑色盒中有7张卡片,其中4张标有数字0,一张标有数字1,两张标有数字2。现从红色盒中任意取1张卡片(每张卡片被抽出的可能性相等),黑色盒中任意取2张卡片(每张卡片抽出的可能性相等),共取3张卡片。
(Ⅰ)求取出的3张卡片都标有数字0的概率;
(Ⅱ)求取出的3张卡片数字之积是4的概率;
(Ⅲ)求取出的3张卡片数字之积是0的概率.
15.(本小题满分12分)
已知A、B两点的坐标分别为
(Ⅰ)求|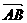 |的表达式;
|的表达式;
|
 (O为坐标原点),求
(O为坐标原点),求 的值;
的值;
(Ⅲ)若 ,求函数
,求函数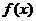 的最大值和最小值。
的最大值和最小值。
14.已知P是双曲线 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
①双曲线的一条准线被它的两条渐近线所截得的线段长度为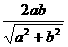 ;
;
②若|PF1|=e|PF2|,则e的最大值为 ;
;
③△PF1F2的内切圆的圆心横坐标为a;
④若直线PF1的斜率为k,则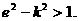
其中正确命题的序号是 。
13.实数x,y满足不等式组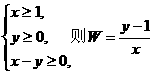 的取值范围是
。
的取值范围是
。
12.若函数 的最小值是 .
的最小值是 .
11.已知球O的一个截面的面积为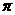 ,球心O到这个截面的距离为1,则该球的半径为
,球心O到这个截面的距离为1,则该球的半径为
,该球的体积为 。
9.若 的展开式中含
的展开式中含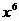 项的系数是448,则正实数
项的系数是448,则正实数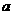 的值为
。
的值为
。
|
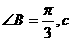 边长为4,a边长为6,则b边长为
, △ABC的面积为
。
边长为4,a边长为6,则b边长为
, △ABC的面积为
。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com