
题目列表(包括答案和解析)
13.球的组合体
(1)球与长方体的组合体:
长方体的外接球的直径是长方体的体对角线长.
(2)球与正方体的组合体:
正方体的内切球的直径是正方体的棱长, 正方体的棱切球的直径是正方体的面对角线长, 正方体的外接球的直径是正方体的体对角线长.
(3) 球与正四面体的组合体:
棱长为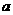 的正四面体的内切球的半径为
的正四面体的内切球的半径为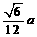 ,
,
外接球的半径为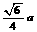 .
.
12.球的半径是R,则
其体积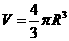 ,其表面积
,其表面积 .
.
11.棱锥的平行截面的性质
如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点到截面距离与棱锥高的平方比(对应角相等,对应边对应成比例的多边形是相似多边形,相似多边形面积的比等于对应边的比的平方);相应小棱锥与小棱锥的侧面积的比等于顶点到截面距离与棱锥高的平方比.
10. 斜棱柱的直截面
已知斜棱柱的侧棱长是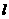 ,侧面积和体积分别是
,侧面积和体积分别是 和
和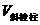 ,它的直截面的周长和面积分别是
,它的直截面的周长和面积分别是 和
和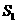 ,则
,则
①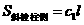 .②
.②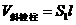 .
.
9. 面积射影定理 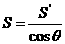 .(平面多边形及其射影的面积分别是
.(平面多边形及其射影的面积分别是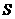 、
、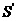 ,它们所在平面所成锐二面角的为
,它们所在平面所成锐二面角的为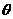 ).
).
8. 长度为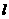 的线段在三条两两互相垂直的直线上的射影长分别为
的线段在三条两两互相垂直的直线上的射影长分别为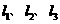 ,夹角分别为
,夹角分别为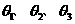 ,则有
,则有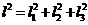
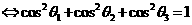
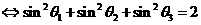 .
.
(长方体对角线长的公式是特例.
7.三余弦定理
设AC是α内的任一条直线,且BC⊥AC,垂足为C,又设AO与AB所成的角为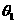 ,AB与AC所成的角为
,AB与AC所成的角为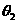 ,AO与AC所成的角为
,AO与AC所成的角为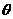 .则
.则 .
.
6.证明平面与平面的垂直的思考途径
(1)转化为判断二面角是直二面角;
(2)转化为线面垂直.
5.证明直线与平面垂直的思考途径
(1)转化为该直线与平面内任一直线垂直;
(2)转化为该直线与平面内相交二直线垂直;
(3)转化为该直线与平面的一条垂线平行;
(4)转化为该直线垂直于另一个平行平面;
(5)转化为该直线与两个垂直平面交线垂直.
4.证明直线与直线的垂直的思考途径
(1)转化为相交垂直;
(2)转化为线面垂直;
(3)转化为线与另一线的射影垂直;
(4)转化为线与形成射影的斜线垂直.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com