
题目列表(包括答案和解析)
3.过抛物线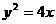 的焦点的弦AB两端点的横坐标分别是
的焦点的弦AB两端点的横坐标分别是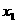 、
、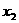 ,若
,若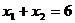 ,则|AB| 的长为
,则|AB| 的长为
(A)10 (B)8 (C)6 (D)7
2.已知 、
、 为两个非零向量,有以下命题:①
为两个非零向量,有以下命题:①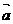 2=
2= 2 ②
2 ② ·
· =
= 2 ③|
2 ③|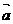 |=|
|=| |且
|且 //
// ,其中可以作
,其中可以作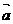 =
= 的必要但不充分条件的命题的
的必要但不充分条件的命题的
(A)② (B)①③ (C)②③ (D)①②③
1.设集合 ,
, 则满足
则满足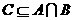 的集合C的个数是
的集合C的个数是
(A)0 (B)1 (C)2 (D)3
6、18(本小题满分12分)
F表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生
产能耗Y(吨标准煤)的几组对照数据
|
|
3 |
4 |
5 |
6 |
|
y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,崩最小二乘法求出Y关于x的线性回归方程Y=bx+a;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性
同归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
解:(1)如图

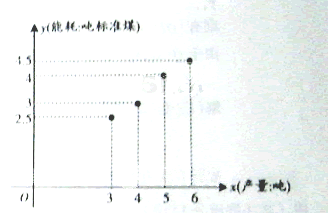
(2)由对照数据,计算得: 
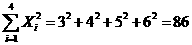
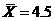
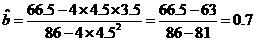 ;
; 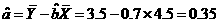
所求的回归方程为 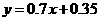
(3) 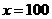 ,
, 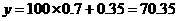 吨,
吨,
预测生产100吨甲产品的生产能耗比技改前降低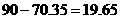 (吨)
(吨)
5、(宁夏理11文12).甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表
|
甲的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
5 |
5 |
5 |
5 |
|
乙的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
6 |
4 |
4 |
6 |
|
丙的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
4 |
6 |
6 |
4 |
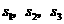 分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( B )
分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( B )
A.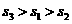 B.
B.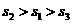
C.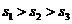 D.
D.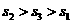
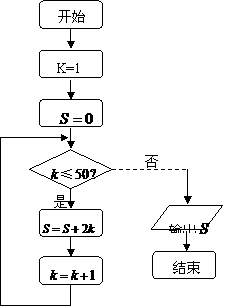
4、(海南文、理5)如果执行下面的程序框图,那么输出的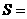 ( C )
( C )
A.2450 B.2500 C.2550 D.2652
1、
 (广东文7、艺术理6)上面左图是某县参加2007
(广东文7、艺术理6)上面左图是某县参加2007
年高考的学生身高条形统计图,从左到右的各
条形表示的学生人数依次记为A1、A2、…、A10
(如A2表示身高(单位:cm)(150,155)内
的学生人数).右图是统计左图中身高在一定范
围内学生人数的一个算法流程图.现要统计身高
在160~180cm(含160cm,不含180cm)的学生人数,
那么在流程图中的判断框内应填写的条件是(B)
A.i<6 B. i<7 C. i<8 D. i<9
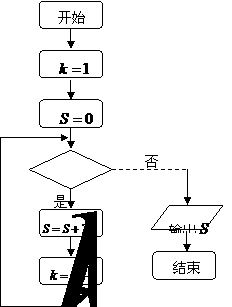 2、(宁夏文、理5).如果执行右面的程序框图,那么输出的
2、(宁夏文、理5).如果执行右面的程序框图,那么输出的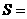 ( C )
( C )
A.2450 B.2500
C.2550 D.2652
(17)(本小题满分12分)
设数列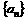 满足a1+2a1+32a1+…+3n-1an=
满足a1+2a1+32a1+…+3n-1an=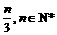 .
.
(Ⅰ)求数列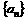 的通项;
的通项;
(Ⅱ)设bn=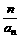 ,求数列
,求数列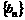 的前n项和Sn.
的前n项和Sn.
(20)(本小题满分12分)
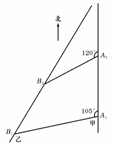 如图,甲船以每小时30
如图,甲船以每小时30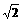 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A1处时,乙船航行到甲船的北偏西120°方向的B1处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A1处时,乙船航行到甲船的北偏西120°方向的B1处,此时两船相距10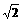 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
(21)(本小题满分12分)
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3;最小值为1;
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l1y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求出该定点的坐标.
]
(22)(本小题满分14分)
设函数f(x)=x2+b ln(x+1),其中b≠0.
(Ⅰ)当b>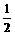 时,判断函数f(x)在定义域上的单调性;
时,判断函数f(x)在定义域上的单调性;
(Ⅱ)求函数f(x)的极值点;
(Ⅲ)证明对任意的正整数n,不等式ln(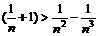 )都成立.
)都成立.
(13)设O是坐标原点,F是抛物线y2=2px(p>0)的焦点,A是抛物线上的一点,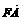 与x轴正向的夹角为60°,则
与x轴正向的夹角为60°,则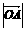 为
.
为
.
(14)设D是不等式组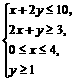 表示的平面区域,则D中的点P(x,y)到直线x+y=10距离的最大值是
.
表示的平面区域,则D中的点P(x,y)到直线x+y=10距离的最大值是
.
(15)与直线x+y-2=0和曲线x2+y2-12x-12y+64=0都相切的半径最小的圆的标准方程是 .
(16)函数y=loga(x+3)-1(a>0,a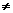 1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则
1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则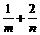 的最小值为
.
的最小值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com