
题目列表(包括答案和解析)
2.已知数列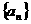 的前n项和为
的前n项和为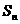 ,且
,且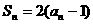 , 则
, 则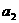 等于
( )
等于
( )
A.4 B.2 C.1 D. -2
1.已知集合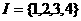 ,
, 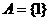 ,
,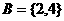 , 则A
, 则A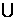 (
(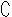 I B)=
( )
I B)=
( )
A.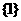 B.
B.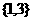 C.
C. 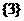 D.
D.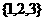
20. (14分)已知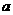 是实数,函数
是实数,函数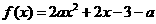 .如果函数
.如果函数 在区间
在区间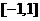 上有
上有
零点,求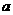 的取值范围.
的取值范围.
解析1:函数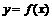 在区间[-1,1]上有零点,即方程
在区间[-1,1]上有零点,即方程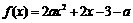 =0在[-1,1]上有解,
=0在[-1,1]上有解,
a=0时,不符合题意,所以a≠0,方程f(x)=0在[-1,1]上有解<=>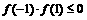 或
或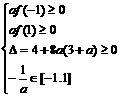
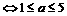 或
或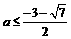 或
或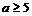

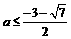 或a≥1.
或a≥1.
所以实数a的取值范围是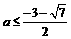 或a≥1.
或a≥1.
解析2:a=0时,不符合题意,所以a≠0,又
∴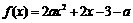 =0在[-1,1]上有解,
=0在[-1,1]上有解,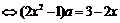 在[-1,1]上有解
在[-1,1]上有解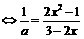 在[-1,1]上有解,问题转化为求函数
在[-1,1]上有解,问题转化为求函数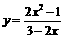 [-1,1]上的值域;设t=3-2x,x∈[-1,1],则
[-1,1]上的值域;设t=3-2x,x∈[-1,1],则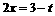 ,t∈[1,5],
,t∈[1,5],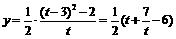 ,
,
设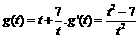 ,
,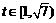 时,
时,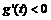 ,此函数g(t)单调递减,
,此函数g(t)单调递减,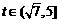 时,
时,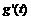 >0,此函数g(t)单调递增,∴y的取值范围是
>0,此函数g(t)单调递增,∴y的取值范围是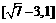 ,∴
,∴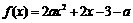 =0在[-1,1]上有解ó
=0在[-1,1]上有解ó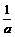 ∈
∈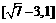
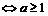 或
或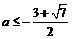 .
.
19.(14分)已知f(x)是定义在[-1,1]上的奇函数,且f (1)=1,若m,n∈[-1,1],m+n≠0时有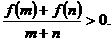
(1)判断f (x)在[-1,1]上的单调性,并证明你的结论; (2)解不等式: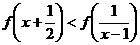 ;
;
(3)若f (x)≤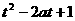 对所有x∈[-1,1],
对所有x∈[-1,1],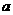 ∈[-1,1]恒成立,求实数t的取值范围.
∈[-1,1]恒成立,求实数t的取值范围.
解:(1)任取-1≤x1<x2≤1,则
f (x1)-f (x2)= f (x1)+f (-x2)=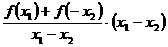
∵-1≤x1<x2≤1,∴x1+(-x2)≠0,
由已知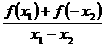 >0,又x1-x2<0,
>0,又x1-x2<0,
∴f (x1)-f (x2)<0,即f (x)在[-1,1]上为增函数.
(2)∵f (x)在[-1,1]上为增函数,故有

(3)由(1)可知:f(x)在[-1,1]上是增函数,且f (1)=1,故对x∈[-l,1],恒有f(x)≤1.
所以要使f(x)≤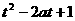 ,对所有x∈[-1,1],
,对所有x∈[-1,1],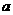 ∈[-1,1]恒成立,
∈[-1,1]恒成立,
即要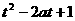 ≥1成立,故
≥1成立,故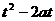 ≥0成立.
≥0成立.
记g(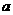 )=
)=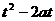 对
对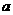 ∈[-1,1],g(
∈[-1,1],g(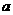 )≥0恒成立,只需g(
)≥0恒成立,只需g(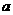 )在[-1,1]上的最小值
)在[-1,1]上的最小值
大于等于零.
故 解得:t≤-2或t=0,或
解得:t≤-2或t=0,或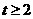
18.(13分)某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米造价45元,屋顶每平方米造价20元,试计算:
(1)仓库表面积S的最大允许值是多少?(2)为使S达到最大值,而实际投资又不超过预算,那么正面铁栅应设计为多长?
答案(1)100平方米 (2)15米
17.(13分)已知二次函数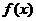 的二次项系数为
的二次项系数为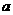 ,且不等式
,且不等式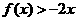 的解集为
的解集为 。
。
(Ⅰ)若方程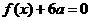 有两个相等的根,求
有两个相等的根,求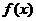 的解析式;
的解析式;
(Ⅱ)若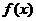 的最大值为正数,求
的最大值为正数,求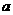 的取值范围。
的取值范围。
答案:(1)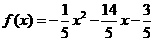 (2)
(2)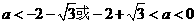
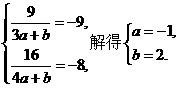
16. (13分)已知函数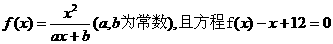 有两个实根为
有两个实根为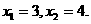
(1)求函数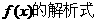 ;
;
(2)设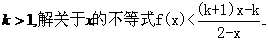
答案:解:(1)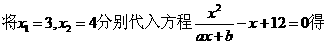
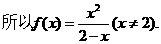
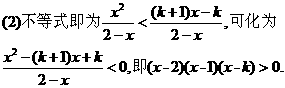
1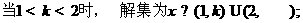
2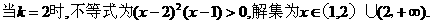
3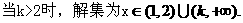
15.(13分) 已知全集为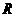 ,
,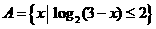 ,
,  , 求
, 求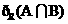
解:∵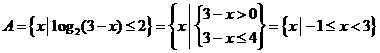
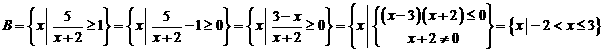 ∴
∴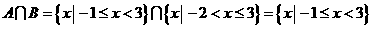
∴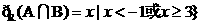
14.汽车在行驶过程中,汽油平均消耗率g(即每小时的汽油耗油量,单位:L/h)与汽车行驶的平均速度v(单位:km/h)之间有所示的函数关系:
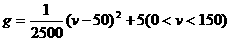
“汽油的使用率最高”(即每千米汽油平均消耗量最小,单位:L/km),则汽油的使用率最高时,汽车速度是 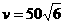 (km/h)
(km/h)
13.已知变量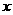 ,
,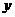 满足约束条件
满足约束条件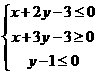 。若目标函数
。若目标函数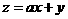 (其中
(其中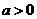 )仅在点
)仅在点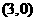 处取得最大值,则
处取得最大值,则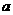 的取值范围为
的取值范围为  。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com