
题目列表(包括答案和解析)
3. 直线的斜率:
定义:倾斜角不是90°的直线,其倾斜角的正切,叫做这条直线的斜率。
符号:常用k表示,即k=tanα。
注意:(1)所有直线都有倾斜角,但不是所有直线都有斜率。
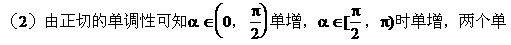
调区间。
(3)当倾斜角为90°时斜率不存在,但直线存在。
2. 直线的倾斜角:
定义:在平面直角坐标系中,对于一条与x轴相交的直线,如果把x轴绕交点逆时针旋转与直线重合时,所转过的最小正角为直线倾斜角。
规定:当直线与x轴平行或重合时,倾斜角为0°。
范围:0°≤α<180°
注意:(1)定义分两部分:一部分是与x轴相交,另一部分与x轴平行。
(2)与x轴相交的定义中,应理解三个地方:①x轴绕交点旋转;②逆时针方向;③最小正角。
(3)应特别注意倾斜角的范围[0,π)。
(4)任何一条直线有唯一倾斜角,表示直线的倾斜程度,但倾斜角为α的直线有无穷多条。
直线的倾斜角和斜率、直线方程的点斜式、直线方程的斜截式
[知识点]
1. 直线的方程和方程的直线:
定义:
(1)以一个方程f(x,y)=0的解为坐标的点都在直线l上。
(2)直线l上的点的坐标都是方程f(x,y)=0的解。
满足(1)(2)的方程f(x,y)=0是直线l的方程,同时称直线l为方程f(x,y)=0的直线。
6. 两直线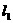 :
: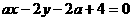 ,和
,和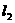 :
: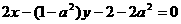 ,当
,当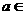 (0,2)时,求直线与两坐标轴围成四边形面积的最小值。
(0,2)时,求直线与两坐标轴围成四边形面积的最小值。
5. 已知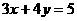 ,
,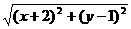 的最小值为( )
的最小值为( )
A. 1 B. 2 C. 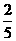 D.
D. 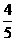
4. 已知A(3,5)B(2,15)在直线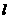 :
: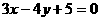 上,找一点P使
上,找一点P使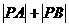 最小,则最小值为( )
最小,则最小值为( )
A. 18 B. 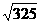 C. 19 D.
C. 19 D. 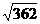
3. 过A(2,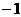 )与原点距离最远的直线方程为( )
)与原点距离最远的直线方程为( )
A. 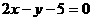 B.
B.
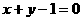
C. 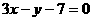 D.
D.
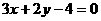
2. 已知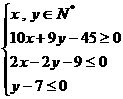 ,则
,则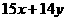 的最小值为( )
的最小值为( )
A. 68 B. 69 C. 70 D. 71
1. 直线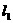 :
: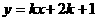 ,
,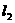 :
: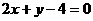 的交点在第一象限,则
的交点在第一象限,则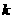 的取值范围是( )
的取值范围是( )
A. 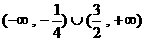 B.
B.
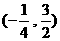
C. 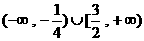 D.
D.
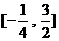
2. 对称
P(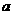 ,
,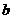 )关于点
)关于点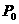 (
(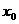 ,
,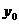 )的对称点为:Q(
)的对称点为:Q(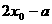 ,
,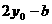 )
)
P(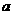 ,
,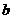 )关于
)关于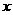 轴的对称点为Q(
轴的对称点为Q(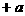 ,
,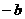 )
)
P(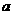 ,
,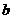 )关于
)关于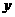 轴的对称点为Q(
轴的对称点为Q(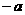 ,
,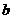 )
)
P(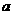 ,
,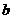 )关于
)关于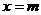 的对称点为Q(
的对称点为Q(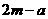 ,
,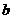 )
)
P(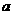 ,
,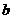 )关于
)关于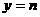 的对称点为Q(
的对称点为Q(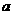 ,
,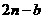 )
)
P(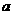 ,
,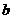 )关于
)关于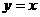 的对称点为Q(
的对称点为Q(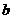 ,
,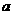 )
)
P(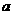 ,
,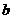 )关于
)关于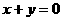 的对称点为Q(
的对称点为Q(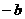 ,
,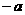 )
)
[典型例题]
[例1] 求点A(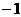 ,4)关于直线
,4)关于直线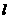 :
: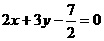 的对称点。
的对称点。
解:
设A关于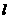 的对称点B(
的对称点B(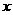 ,
,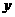 )
)
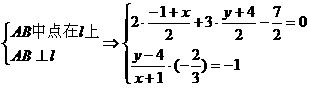 ∴ B(
∴ B(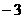 ,
,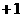 )
)
[例2] 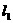 :
: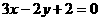 ,
,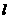 :
: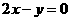 ,求
,求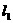 关于
关于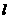 对称的直线
对称的直线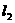 的方程。
的方程。
解:
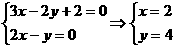
A(0,1)在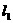 点,它关于
点,它关于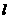 的对称点,B(
的对称点,B(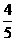 ,
,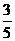 )
)
由两点式 ∴ 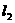 :
: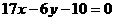
[例3] 光线通过点P(2,3)在直线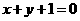 上反射,反射线过点Q(1,1),求入射光线、反射光线所在直线方程。
上反射,反射线过点Q(1,1),求入射光线、反射光线所在直线方程。
解:
(2,3)点关于直线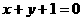 的对称点,
的对称点,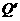 (
(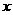 ,
,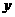 )
)
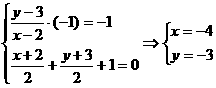
由两点式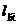 :
: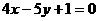
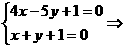 交点(
交点(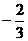 ,
,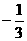 )
)
由两点式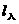 :
: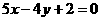
[例4] 正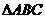 中A(1,1),中心M(5,3),求三边所在直线方程。
中A(1,1),中心M(5,3),求三边所在直线方程。
解:
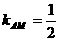 ∴
∴ 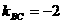 AM交于BC于D,M分
AM交于BC于D,M分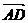 之比
之比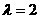
∴ D=(7,4) ∴
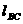 :
: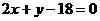
设AB、AC为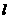 :
: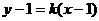
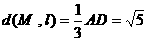
∴ 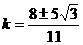
[例5] 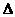 ABC中,A(9,1),B(3,4),内心I(4,1),求C
ABC中,A(9,1),B(3,4),内心I(4,1),求C
解:
AI∥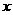 轴 ∴
轴 ∴
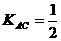 ∴
∴ 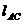 :
: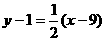
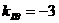 利用三角公式 ∴
利用三角公式 ∴
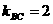
∴ 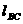 :
: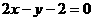 ∴ C(
∴ C(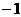 ,4)
,4)
[例6] 已知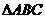 中,A(
中,A(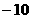 ,2)B(6,4)垂心H(5,2),求C
,2)B(6,4)垂心H(5,2),求C
解:
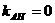 ∴
∴ 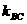 不存在 ∴
不存在 ∴ 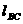
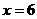
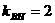
∴ 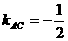 ∴
∴ 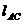 :
: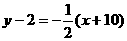
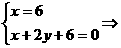 C(6,
C(6,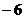 )
)
[例7] 已知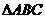 ,A(6,3),B(
,A(6,3),B(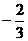 ,
,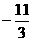 ),C(
),C(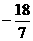 ,
,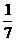 )求
)求 。
。
解:
作图, 为BC到HC的角 ∴
为BC到HC的角 ∴ 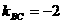
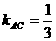
∴ 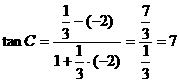 ∴
∴ 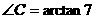
[例8] 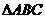 中,AB、BC、CA边的中点为D(
中,AB、BC、CA边的中点为D(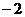 ,
,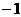 )E(1,3)F(2,0),求三边所在直线方程。
)E(1,3)F(2,0),求三边所在直线方程。
解:
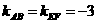 ∴
∴ 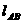 :
: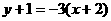 即
即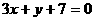
同理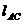 :
: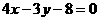
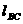 :
: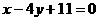
[例9] 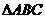 ,A(
,A(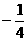 ,
,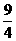 )、B(6,
)、B(6,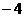 )、C(
)、C(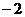 ,
,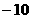 ),求
),求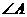 的角平分线AT所在直线方程。
的角平分线AT所在直线方程。
解:
设斜率为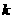
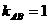
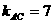 CA到AT的角等于AT到AB的角
CA到AT的角等于AT到AB的角
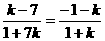
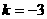 或
或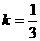 (舍,结合图形)
(舍,结合图形)
∴ 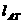 :
: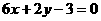
[例10] 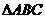 中,A(
中,A(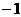 ,
,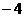 )两条中线所在直线方程为
)两条中线所在直线方程为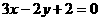 ,
,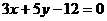 ,求BC边所在直线方程。
,求BC边所在直线方程。
解:
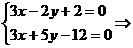 G(
G(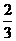 ,2) G分
,2) G分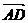 之比
之比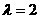 ∴ D(
∴ D(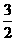 ,5)
,5)
设B(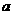 ,
,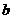 ) ∴ C(
) ∴ C(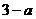 ,
,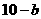 )
)
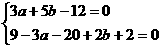
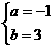 ∴ 两点式:
∴ 两点式: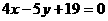
[模拟试题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com