
题目列表(包括答案和解析)
22.解:(1) ,
,
∵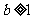 ,∴
,∴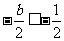 ,故当
,故当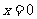 时,
时,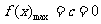 。……………………………2分
。……………………………2分
若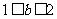 ,∴
,∴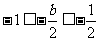 ,则
,则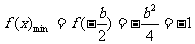 ,∴
,∴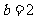
若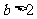 ,则
,则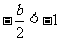 ,则
,则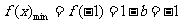 ,∴
,∴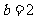 (舍去)
(舍去)
故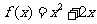 ……………………………………4分
……………………………………4分
(2)当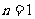 时,
时,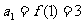 ,
,
当 时,
时,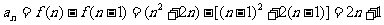
∴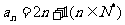 …………………………………………………6分
…………………………………………………6分
∴ ,
,
∴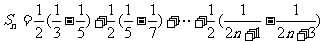
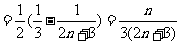
∴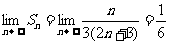 ……………………………………………9分
……………………………………………9分
(3)∵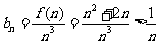 ……………………………………………10分
……………………………………………10分
∴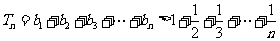 ,
,
∵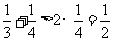 ,
,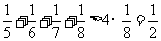 ,…………
,…………
 ,
,
故当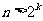 时,
时,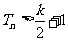 ,
,
因此,对任何常数A,设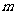 是不小于A的最小正整数,
是不小于A的最小正整数,
则当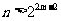 时,必有
时,必有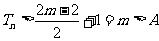 。
。
故不存在常数A使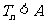 对所有
对所有 的正整数恒成立。……………………14分
的正整数恒成立。……………………14分
21.(本小题满分12分)。
(1)解:依题意,可设所求抛物线方程为: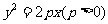
则抛物线的准线方程为: ,∴点M(2,y)到准线的距离
,∴点M(2,y)到准线的距离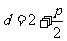 ,……2分
,……2分
由抛物线定义知: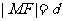 ,故
,故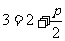 ,∴
,∴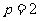 ,
,
故所求抛物线方程为: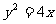 。………………4分
。………………4分
(2)证明:依题意,可设直线AB的方程为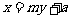 ,代入抛物线方程
,代入抛物线方程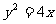 得:
得:
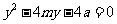 ,①
,①
设A、B两点的坐标分别是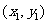 、
、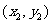 ,则
,则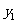 、
、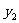 是方程①的两根,
是方程①的两根,
∵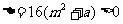 ,∴
,∴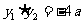 ………………6分
………………6分
由点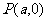 分有向线段
分有向线段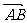 所成的比为
所成的比为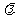 得:
得: ,即
,即 ,
,
又点Q是点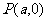 关于原点的对称点,故点Q的坐标是
关于原点的对称点,故点Q的坐标是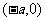 ,从而
,从而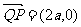 ,
,
∵
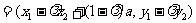 ,
,
∴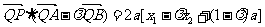 …………………………………9分
…………………………………9分
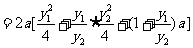
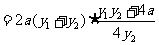
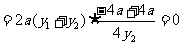 ,
,
∴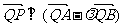 。………………………………………12分。
。………………………………………12分。
20.解:(1)设从第一辆车投入施工算起,各车到达时间依此为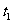 、
、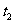 、…、
、…、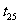 ,依题意,它们组成一个首项为0,公差为
,依题意,它们组成一个首项为0,公差为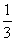 (小时)的等差数列,…………3分
(小时)的等差数列,…………3分
则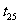 =
=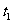 +24d,∴
+24d,∴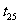 =24×
=24×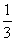 =8,
=8,
答:第25辆车须8小时后才能到达。………………6分
(2)设从第一辆车投入施工算起,各车的工作时间依次为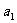 、
、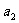 、…、
、…、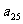 ,依题意,它们组成一个公差为-
,依题意,它们组成一个公差为-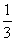 (小时)的等差数列,且
(小时)的等差数列,且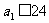 ………………8分
………………8分
∵每辆车每小时的工作效率为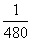 ,∴
,∴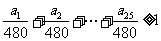
即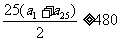 ,……………………10分
,……………………10分
又∵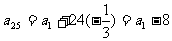 ,∴
,∴ ,即
,即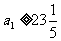 ,
,
由于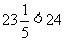 ,可见
,可见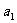 的工作时间可以满足要求,即工程可以在24小时内完成。
的工作时间可以满足要求,即工程可以在24小时内完成。
答:24小时内能完成防洪堤坝。………………………………………………12分
19.解:(1)在直三棱柱ABC-A1B1C1中,
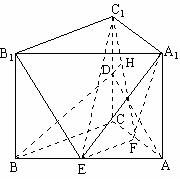 (1)∵
(1)∵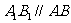 ,
,
∴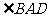 (或其补角)为异面直线AD与A1B1所成的角,
(或其补角)为异面直线AD与A1B1所成的角,
………………………2分,连结BD,
在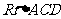 中,∵AC=4,
中,∵AC=4,
∴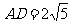 ,
,
在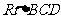 中,∵BC=3,CD=2,∴
中,∵BC=3,CD=2,∴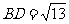 ,
,
在△ABD中,∵AB=5,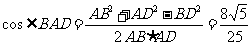
∴异面直线AD与A1B1所成角的余弦值为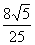 ………………………………4分
………………………………4分
(2)证明:∵AB=5,BC=3,AC=4,∴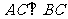 ,
,
∵底面ABC⊥侧面ACC1A1,∴BC⊥侧面ACC1A1,………………………………6分
取AB、AC的中点E、F,连结EF、A1F,则EF//BC,
∴EF⊥平面ACC1A1, ∴A1F为A1E在侧面AC1内的射影,
在正方形C1CAA1内,∵ D、F分别为CC1、AC的中点,
∴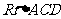 ≌
≌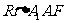 ,∴
,∴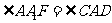 ,
,
∴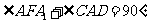 ,∴
,∴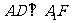 ,
,
∴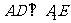 (三垂线定理)………………8分
(三垂线定理)………………8分
(3)连结 ,过D作DH⊥
,过D作DH⊥ ,垂足为H。
,垂足为H。
∵EF//BC,BC//B1C1,∴EF// B1C1,∴点F在平面B1C1E内。
∵EF⊥平面ACC1A1, 平面ACC1A1,EF⊥DH,………………10分
平面ACC1A1,EF⊥DH,………………10分
∵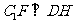 ,
,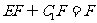 ,∴DH⊥平面B1C1E。
,∴DH⊥平面B1C1E。
在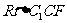 中,∵
中,∵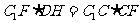 ,∴
,∴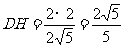 。……………12分
。……………12分
18.解:(1)∵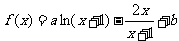 ,∴
,∴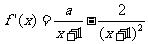 , ……2分
, ……2分
∵函数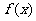 在
在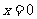 处的切线方程为
处的切线方程为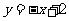 ,
,
∴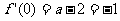 ,∴
,∴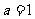 ……………………………………………………5分
……………………………………………………5分
(2)∵点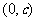 在直线
在直线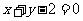 上, ∴
上, ∴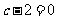 ,∴
,∴ ,
,
∵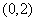 在
在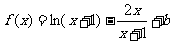 的图象上,∴
的图象上,∴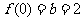 ,
,
∴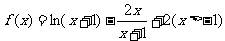 …………………………………………7分
…………………………………………7分
由(1)得: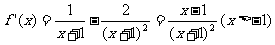 ,
,
令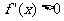 ,则
,则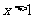 ,因此函数
,因此函数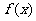 的单调递增区间为(1,+∞),……9分
的单调递增区间为(1,+∞),……9分
令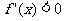 ,则
,则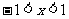 ,因此函数
,因此函数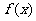 的单调递减区间为(-1,1)
的单调递减区间为(-1,1)
∴当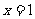 时,函数
时,函数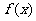 取得极小值
取得极小值 ………………………………………12分
………………………………………12分
17.解:∵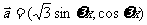 ,
,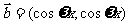
∴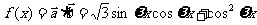 ………………………2分
………………………2分
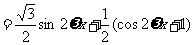 ………………………4分
………………………4分
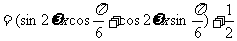
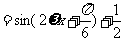 ………………………6分
………………………6分
(1)∵函数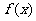 的最小正周期
的最小正周期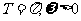 ,
,
∴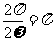 ,∴
,∴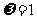 ………………………8分
………………………8分
(2)当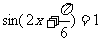 时,函数
时,函数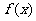 取得最大值
取得最大值 ,
,
此时,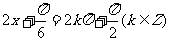 ,解得
,解得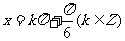 ……………12分
……………12分
13.495 14.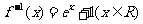 15.16
15.16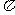 16.
16.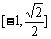
1.A 2.D 3.D 4.B 5.D 6.C 7.C 8.B 9.B 10.A 11.A 12.B
22.(本小题满分14分)
已知函数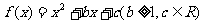 ,若
,若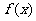 的定义域为[-1,0],值域也为
的定义域为[-1,0],值域也为
[-1,0]。
(1)求出符合条件的函数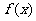 的表达式;
的表达式;
(2)若数列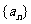 的前
的前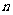 项和为
项和为 ,数列
,数列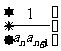 的前
的前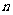 项和为
项和为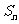 ,试求
,试求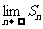 ;
;
(3)若数列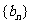 满足
满足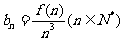 ,记数列
,记数列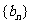 的前
的前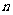 项和为
项和为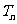 ,问是否存在正常数A,使得对于任意正整数
,问是否存在正常数A,使得对于任意正整数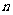 都有
都有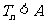 ?并证明你的结论。
?并证明你的结论。
参考解答及评分标准
21.(本小题满分12分)
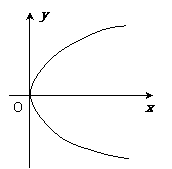 已知抛物线的顶点在原点,焦点F在
已知抛物线的顶点在原点,焦点F在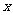 轴上。M为抛物线上的点,M的横坐标为2,且|MF|=3。
轴上。M为抛物线上的点,M的横坐标为2,且|MF|=3。
(1)求此抛物线的方程;
(2)如图,过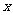 轴正半轴上任一点
轴正半轴上任一点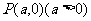 作直线与此抛物线交于A、B两点,点Q是点P关于原点的对称点。点P分有向线段
作直线与此抛物线交于A、B两点,点Q是点P关于原点的对称点。点P分有向线段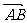 所成的比为
所成的比为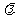 。
。
求证: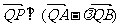 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com