
题目列表(包括答案和解析)
2.在各项都为正数的等比数列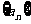 中,首项
中,首项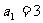 ,前三项和为21,则
,前三项和为21,则 =( )
=( )
A.33 B.72 C.84 D.189
1.已知等差数列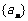 中,
中,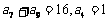 ,则
,则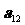 的值是(
)
的值是(
)
A.15 B.30 C.31 D.64
4.已知数列{an}的前n项和Sn满足:Sn=2an +(-1)n,n≥1.
⑴写出求数列{an}的前3项a1,a2,a3;
⑵求数列{an}的通项公式;
⑶证明:对任意的整数m>4,有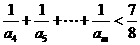 .
.
3.设数列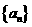 满足
满足
(1)
证明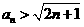 对一切正整数n 成立;
对一切正整数n 成立;
令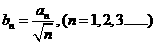 ,判断
,判断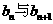 的大小,并说明理由。
的大小,并说明理由。
2.设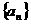 是一个公差为
是一个公差为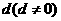 的等差数列,它的前10项和
的等差数列,它的前10项和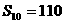 且
且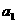 ,
,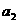 ,
,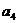 成等比数列。
成等比数列。
(1)证明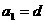 ;(2)求公差
;(2)求公差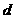 的值和数列
的值和数列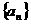 的通项公式。
的通项公式。
1.已知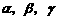 成公比为2的等比数列
成公比为2的等比数列
(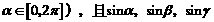 也成等比数列. 求
也成等比数列. 求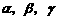 的值.
的值.
6.若干个能唯一确定一个数列的量称为该数列的“基本量”.设{an}是公比为q的无穷等比数列,下列{an}的四组量中,一定能成为该数列“基本量”的是第 组.(写出所有符合要求的组号)
①S1与S2; ②a2与S3; ③a1与an; ④q与an.
其中n为大于1的整数, Sn为{an}的前n项和.
5.设数列{an}的前n项和为Sn,Sn=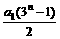 (对于所有n≥1),且a4=54,则a1的数值是____________.
(对于所有n≥1),且a4=54,则a1的数值是____________.
4.定义“等和数列”:在一个数列中,如果每一项与它后一项的和都为同一常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。
已知数列{ an}为等和数列,且a1 =2,公和为5,那么a18的值为_____________,这个数列的前n项和的计算公式为______________________________。
3.在等差数列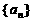 中,当
中,当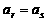
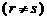 时,
时,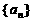 必定是常数数列。然而在等比数列
必定是常数数列。然而在等比数列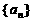 中,对某些正整数
中,对某些正整数 、
、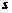
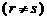 ,当
,当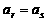 时,非常数数列
时,非常数数列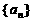 的一个例子是________________________________________.
的一个例子是________________________________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com