
题目列表(包括答案和解析)
8.已知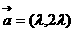 ,
,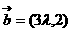 ,如果
,如果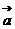 与
与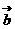 的夹角为锐角,则
的夹角为锐角,则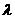 的取值范围是______(答:
的取值范围是______(答: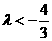 或
或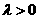 且
且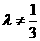 );
);
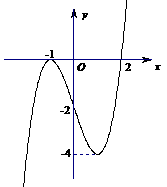
7.函数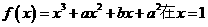 处有极小值10,则a+b的值为____(答:-7)
处有极小值10,则a+b的值为____(答:-7)
6.已知函数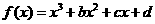 在区间[-1,2
]上是减函数,那么b+c有最__值__答:大,
在区间[-1,2
]上是减函数,那么b+c有最__值__答:大,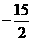 )
)
5.已知函数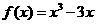 过点
过点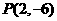 作曲线
作曲线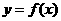 的切线,求此切线的方程(答:
的切线,求此切线的方程(答: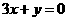 或
或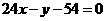 )。
)。
4.(1)设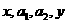 成等差数列,
成等差数列,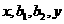 成等比数列,则
成等比数列,则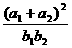 的取值范围是____________.(答:
的取值范围是____________.(答: )。
)。
(2)设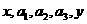 成等差数列,
成等差数列,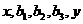 成等比数列,则
成等比数列,则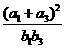 的取值范围是____________.(答:
的取值范围是____________.(答: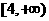 )。
)。
3.如若函数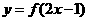 是偶函数,则函数
是偶函数,则函数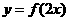 的对称轴方程是__ (答:
的对称轴方程是__ (答: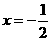 ).
).
2.函数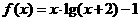 的图象与
的图象与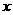 轴的交点个数有____个(答:2)
轴的交点个数有____个(答:2)
1.定义在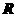 上的偶函数
上的偶函数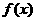 满足
满足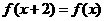 ,且在
,且在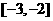 上是减函数,若
上是减函数,若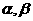 是锐角三角形的两个内角,则
是锐角三角形的两个内角,则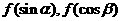 的大小关系为____ (答:
的大小关系为____ (答: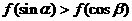 );
);
32.已知三次函数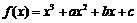 在
在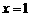 和
和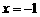 时取极值,且
时取极值,且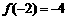 .
.
(1) 求函数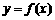 的表达式;
的表达式;
(2) 求函数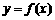 的单调区间和极值;
的单调区间和极值;
(3) 若函数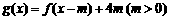 在区间
在区间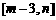 上的值域为
上的值域为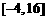 ,试求
,试求 、
、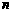 应满足的条件.
应满足的条件.
解:(1) 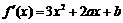 ,
,
 由题意得,
由题意得,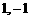 是
是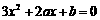 的两个根,
的两个根,
解得,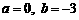 .
.
再由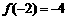 可得
可得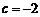 .
.
∴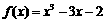 .
.
(2) 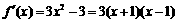 ,
,
当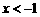 时,
时,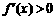 ;当
;当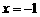 时,
时,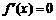 ;
当
;
当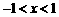 时,
时,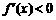 ;当
;当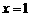 时,
时,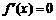 ;
当
;
当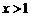 时,
时,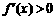 .
.
∴函数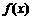 在区间
在区间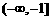 上是增函数;
在区间
上是增函数;
在区间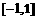 上是减函数;在区间
上是减函数;在区间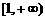 上是增函数.
函数
上是增函数.
函数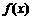 的极大值是
的极大值是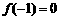 ,极小值是
,极小值是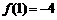 .
.
(3) 函数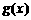 的图象是由
的图象是由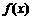 的图象向右平移
的图象向右平移 个单位,向上平移4
个单位,向上平移4 个单位得到的,
个单位得到的,
所以,函数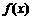 在区间
在区间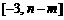 上的值域为
上的值域为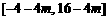 (
(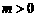 ).
).
而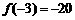 ,∴
,∴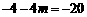 ,即
,即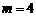 .
.
于是,函数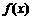 在区间
在区间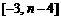 上的值域为
上的值域为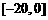 .
.
令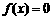 得
得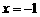 或
或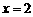 .
.
由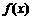 的单调性知,
的单调性知,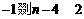 ,即
,即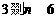 .
.
综上所述, 、
、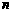 应满足的条件是:
应满足的条件是: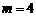 ,且
,且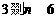 .
.
易错问题
18.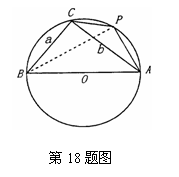 解:(Ⅰ)证明:根据正弦定理得,
解:(Ⅰ)证明:根据正弦定理得,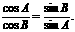
整理为,sinAcosA=sinBcosB,即sin2A=sin2B.
∴2A=2B或2A+2B=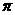 ∴
∴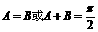 .
.

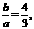 ∴舍去A=B. ∴
∴舍去A=B. ∴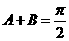 即
即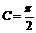 .
.
故△ABC是直角三角形.
(Ⅱ)解:由(1)可得:a=6,b=8.
在Rt△ACB中,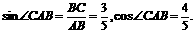
∴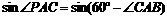
=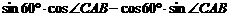
=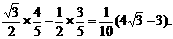
连结PB,在Rt△APB中,AP=AB·cos∠PAB=5.
∴四边形ABCP的面积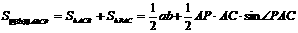
=24+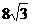
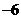 =18+
=18+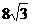 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com