
题目列表(包括答案和解析)
5.
函数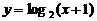 的反函数是
的反函数是
(A) 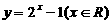 (B)
(B)
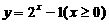
(C) 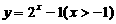 (D)
(D)
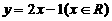
4. 设圆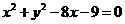 的弦
的弦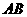 中点为
中点为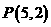 ,则直线
,则直线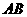 的方程为
的方程为
(A) 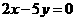 (B)
(B) 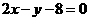 (C)
(C) 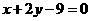 (D)
(D) 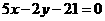
3. 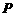 是
是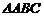 内一点,
内一点, 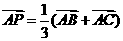 , 则
, 则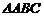 的面积与
的面积与 的面积之比为
的面积之比为
(A) 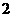 (B)
(B) 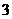 (C)
(C) 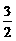 (D)
(D) 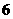
2.
“ 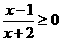 ”是“
”是“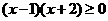 ”的
”的
(A)充要条件 (B)充分不必要条件 (C)必要不充分条件 (D)既不充分也不必要条件
1. 设集合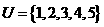 ,
,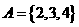 ,
,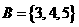 ,则
,则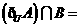
(A) 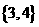 (B)
(B)  (C)
(C) 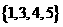 (D)
(D) 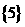
22.(本题满分18分.第(1)题4分,第(2)题6分,第(3)题8分)
已知直线l:y =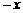 +b与抛物线y2 = 4x相交于A、B两点,︱AB︱= 8.
+b与抛物线y2 = 4x相交于A、B两点,︱AB︱= 8.
(1)求直线l的方程;
(2)求抛物线上横坐标为1的点D与点A、B构成的∆DAB的面积;
(3)设P(x, y)是抛物线上的动点,试用x或y来讨论∆PAB面积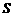 的取值范围.
的取值范围.
21.(本题满分16分,第(1)题4分,第(2)题7分,第(3)题5分)
记函数 ,
,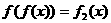 ,它们定义域的交集为
,它们定义域的交集为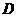 ,若对任意的
,若对任意的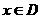 ,
,
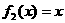 ,则称
,则称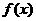 是集合
是集合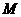 的元素.
的元素.
(1)判断函数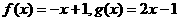 是否是
是否是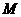 的元素;
的元素;
(2)设函数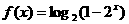 ,求
,求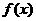 的反函数
的反函数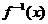 ,并判断
,并判断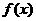 是否是
是否是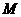 的元素;
的元素;
(3)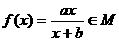 (
(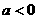 ),求使
),求使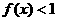 成立的
成立的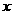 的范围.
的范围.
[解]
20.(本题满分14分,第(1)题7分,第(2)题7分)
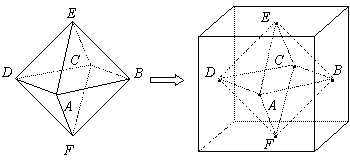
两个相同的正四棱锥底面重合组成一个八面体,可放于棱长为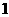 的正方体中,重合的底面与正方体的某一个面平行,各顶点均在正方体的表面上,把满足上述条件的八面体称为正方体的“正子体”.
的正方体中,重合的底面与正方体的某一个面平行,各顶点均在正方体的表面上,把满足上述条件的八面体称为正方体的“正子体”.
(1)若正子体的六个顶点分别是正方体各面的中心,求此正子体的体积;
(2)在(1)的条件下,求异面直线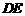 与
与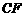 所成的角.
所成的角.
 [解]
[解]
19.(本题满分14分,第(1)题6分,第(2)题8分)
据预测,某旅游景区游客人数在 至
至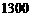 人之间,游客人数
人之间,游客人数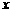 (人)与游客的消费总额
(人)与游客的消费总额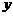 (元)之间近似地满足关系:
(元)之间近似地满足关系: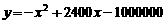 .
.
(1)若该景区游客消费总额不低于 元时,求景区游客人数的范围.
元时,求景区游客人数的范围.
(2)当景区游客的人数为多少人时,游客的人均消费最高?并求游客的人均最高消费额.
[解]
18.(本题满分12分,第(1)题4分,第(2)题8分)
等差数列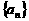 中,前
中,前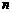 项和为
项和为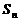 ,首项
,首项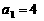 ,
,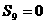 .
.
(1)若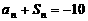 ,求
,求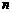 ;
;
(2)设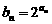 ,求使不等式b1
+ b2 + … + bn > 30的最小正整数
,求使不等式b1
+ b2 + … + bn > 30的最小正整数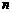 的值.
的值.
[解]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com