
题目列表(包括答案和解析)
5. (★★★★)如图,函数y=
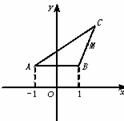
(★★★★)如图,函数y=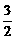 |x|在x∈[-1,1]的图象上有两点A、B,AB∥Ox轴,点M(1,m)(m∈R且m>
|x|在x∈[-1,1]的图象上有两点A、B,AB∥Ox轴,点M(1,m)(m∈R且m>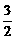 )是△ABC的BC边的中点.
)是△ABC的BC边的中点.
(1)写出用B点横坐标t表示△ABC面积S的函数解析式S=f(t);
(2)求函数S=f(t)的最大值,并求出相应的C点坐标.
4.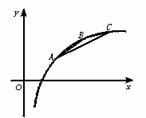 (★★★★)如图,在函数y=lgx的图象上有A、B、C三点,它们的横坐标分别为m,m+2,m+4(m>1).
(★★★★)如图,在函数y=lgx的图象上有A、B、C三点,它们的横坐标分别为m,m+2,m+4(m>1).
(1)若△ABC面积为S,求S=f(m);
(2)判断S=f(m)的增减性.
3.(★★★★★)已知函数f(x)=log2(x+1),将y=f(x)的图象向左平移1个单位,再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数y=g(x)的图象,则函数F(x)=f(x)-g(x)的最大值为_________.
2.(★★★★)某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了,再走余下的路,下图中y轴表示离学校的距离,x轴表示出发后的时间,则适合题意的图形是( )
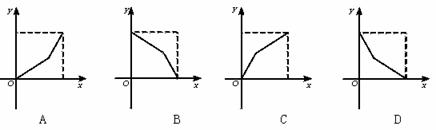
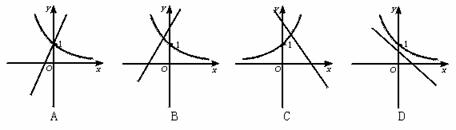
1.(★★★★)当a≠0时,y=ax+b和y=bax的图象只可能是( )
21.(本小题满分14分)
设 f (x) = px--2 ln x,且 f (e) = qe--2(e为自然对数的底数).
(I) 求 p 与 q 的关系;
(II) 若 f (x) 在其定义域内为单调函数,求 p 的取值范围;
(III)设 g(x) = ,若在 [1,e] 上至少存在一点x0,使得 f (x0) > g(x0) 成立, 求实数 p 的取值范围.
20.(本小题共13分)已知 是双曲线
是双曲线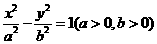 上两点,
上两点, 为原点,直线
为原点,直线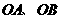 的斜率之积
的斜率之积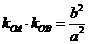
(Ⅰ)设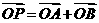 ,证明当
,证明当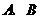 运动时,点
运动时,点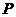 恒在另一双曲线上;
恒在另一双曲线上;
(Ⅱ)设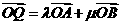 ,是否存在不同时为零的实数
,是否存在不同时为零的实数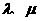 ,使得点
,使得点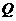 在题设双曲线的渐近线上,证明你的结论.
在题设双曲线的渐近线上,证明你的结论.
19.(本小题满分12分)
某家具城进行促销活动,促销方案是:顾客每消费1000元,便可以获得奖券一张. 每张奖券中奖的概率为 ,若中奖,则家具城返还顾客现金1000元. 某顾客购买一张价格为3400元的餐桌,得到3张奖券. 设该顾客购买餐桌的实际支出为 x (元).
(I) 求 x 的所有可能取值;
(II) 求 x 的分布列和期望。
18.(本小题满分12分) 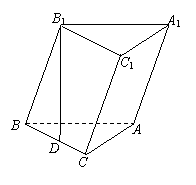 已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α(0°<α<90°),点
已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α(0°<α<90°),点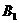 在底面上的射影
在底面上的射影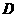 落在
落在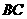 上.
上.
(Ⅰ)求证:AC⊥平面BB1C1C;
(Ⅱ)当α为何值时,AB1⊥BC1,且使D恰为BC中点?
(Ⅲ)若α = arccos ,且AC=BC=AA1时,求二面角C1-AB-C的大小.
17.已知数列 {2 n•an} 的前 n 项和 Sn = 9-6n.
(I) 求数列 {an} 的通项公式;
(II) 设 bn = n·(2-log 2 ),求数列 { } 的前 n 项和Tn.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com