
题目列表(包括答案和解析)
6.等差数列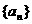 中,
中,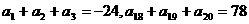 ,则此数列前20项和等于
,则此数列前20项和等于
A.160 B.180 C.200 D.220
5.为了得到函数 的图象,可以把函数
的图象,可以把函数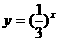 的图象( )
的图象( )
A.向左平移3个单位长度 B.向右平移3个单位长度
C.向左平移1个单位长度 D.向右平移1个单位长度
4. 函数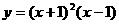 在
在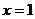 处的导数等于( )
处的导数等于( )
A.1 B.2 C.3 D.4
3.正三棱柱侧面的一条对角线长为2,且与底面成45°角,则此三棱柱的体积为( )
A.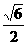 B.
B. 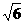 C.
C.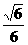 D.
D. 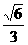
2.函数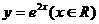 的反函数为( )
的反函数为( )
A.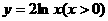 B.
B.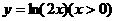
C.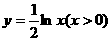 D.
D.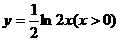
1.设集合U={1,2,3,4,5},集合M={0,3,5},N={1,4,5},则M∩(CU N)=( )
A.{5} B.{0,3} C.{0,2,3,5} D. {0,1,3,4,5}
10.(北师大版第52页例3)应用
变式1: 解:设矩形ABCD在x轴上的边是BC,BC的长是x(0<x<a),
则B点的坐标为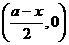 ,A点的坐标为
,A点的坐标为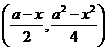 .
.
设矩形ABCD的周长为P,
则P=2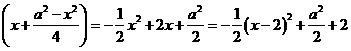 (0<x<a).
(0<x<a).
① 若a>2,则当x=2时,矩形的周长P有最大值,这时矩形两边的长分别为2和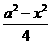 ,两边之比为8:
,两边之比为8: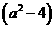 ;
;
②若0 <a≤2,此时函数P=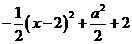 无最大值,也就是说周长最大的内接矩形不存在.
无最大值,也就是说周长最大的内接矩形不存在.
综上所述,当a>2时,周长最大的内接矩形两边之比为8: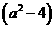 ;当0 <a≤2时,周长最大的内接矩形不存在.
;当0 <a≤2时,周长最大的内接矩形不存在.
变式2: 解:(I) 依题意设 A、B 两种产品的利润表示为投资的函数关系式分别为
f (x) = kx,g(x) = m,
由 f (1) = k = 0.25, g(4) = 2m = 2.5 Þ m = ,
∴ f (x) = x(x≥0),g(x) = .
(II) 设企业在 B 产品投资 x 万元,则在 A 产品投资 10-x 万元,
∴ 企业的利润 y = (10-x) + = [-(-) 2 + ](0≤x≤10),
∴ = ,即 x = 6.25 万元时,企业获得最大利润 ≈4 万元.
答:在 A 产品投资 3.75 万元,在 B 产品投资 6.25 万元,企业获得最大利润约 4 万元.
变式3:
解:设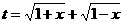 ,要使
,要使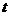 有意义,必须
有意义,必须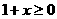 且
且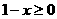 ,即
,即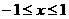 ,
,
∵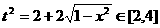 ,且
,且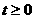 ……①
……①
∴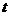 的取值范围是
的取值范围是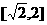 .
.
由①得: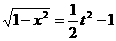 ,
,
不妨设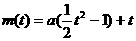
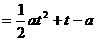 ,
,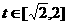 .
.
(I)由题意知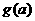 即为函数
即为函数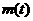
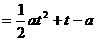 ,
,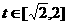 的最大值,
的最大值,
当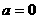 时,
时,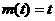 ,
,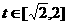 ,有
,有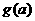 =2;
=2;
当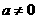 时,此时直线
时,此时直线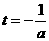 是抛物线
是抛物线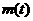
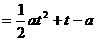 的对称轴,
的对称轴,
∴可分以下几种情况进行讨论:
(1)当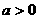 时,函数
时,函数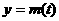 ,
,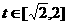 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由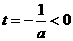 知
知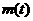 在
在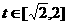 上单调递增,故
上单调递增,故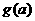
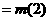
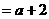 ;
;
(2)当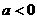 时,,函数
时,,函数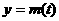 ,
,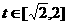 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若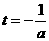
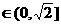 即
即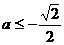 时,
时,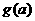
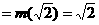 ,
,
若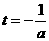
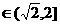 即
即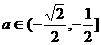 时,
时,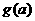
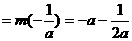 ,
,
若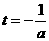
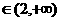 即
即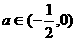 时,
时,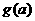
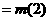
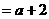 .
.
综上所述,有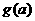 =
=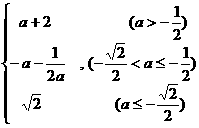 .
.
(II)若a>0,则>0,此时g(a)=g( ) Û a+2= +2 Û a = Þa =1(舍去a=-1);
若-<a<0,则<-2,此时g(a)=g( ) Û a+2=Þ a=-2+<-(舍去);
若-<a≤-,则-2≤<-,
此时g(a)=g( ) Û -a-= Þ a=- (舍去);
若-≤a≤-,则-≤≤-,
此时g(a)=g( ) Û =恒成立;
若-2≤a<-,则-<≤-,
此时g(a)=g( ) Û =-a-Þ a=- (舍去);
若a<-2,则-<<0,
此时g(a)=g( ) Û = a+2Þ a=-2+>-2 (舍去) .
综上所述,满足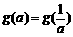 的所有实数a为:
的所有实数a为: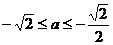 或
或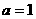 .
.
9.(北师大版第54页B组第1题)根与系数关系
变式1: 解:二次函数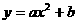 与一次函数图象
与一次函数图象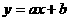 交于两点
交于两点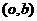 、
、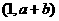 ,由二次函
,由二次函
数图象知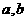 同号,而由
同号,而由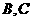 中一次函数图象知
中一次函数图象知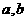 异号,互相矛盾,故舍去
异号,互相矛盾,故舍去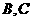 .
.
又由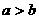 知,当
知,当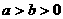 时,
时,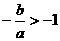 ,此时与
,此时与 中图形不符,当
中图形不符,当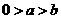 时,
时,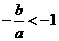 ,与
,与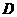 中图形相符.
中图形相符.
变式2: 解:原命题可变为:求方程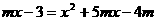 ,
,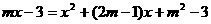 ,
,
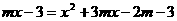 中至少有一个方程有实数解,而此命题的反面是:“三个方程均无实数解”,于是,从全体实数中除去三个方程均无实数解的
中至少有一个方程有实数解,而此命题的反面是:“三个方程均无实数解”,于是,从全体实数中除去三个方程均无实数解的 的值,即得所求.
的值,即得所求.
解不等式组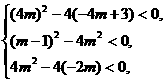 得
得 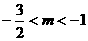 ,
,
故符合条件的 取值范围是
取值范围是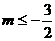 或
或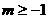 .
.
变式3: 解:(I) 由 f (x) 表达式得 m = -,
∵ g(x) = f (x)-x = a x 2 + (b-1) x + 1,a > 0,
由 x1,x2 是方程 f (x) = x的两相异根,且 x1 < 1 < x2,
∴ g(1) < 0 Þ a + b < 0 Þ -> 1 Þ -> ,即 m > .
(II) △= (b-1) 2-4a > 0 Þ (b-1) 2 > 4a,
x1 + x2 = ,x1x2 = ,
∴ | x1-x2 | 2 = (x1 + x2) 2-4x1x2 = () 2-= 2 2,
∴ (b-1) 2 = 4a + 4a 2 (*)
又 | x1-x2 | = 2,
∴ x1、x2 到 g(x) 对称轴 x = 的距离都为1,
要 g(x) = 0 有一根属于 (-2,2),
则 g(x) 对称轴 x = Î (-3,3),
∴ -3 < < 3 Þ a > | b-1 |,
把代入 (*) 得:(b-1) 2 > | b-1 | + (b-1) 2,
解得:b < 或 b > ,
∴ b 的取值范围是:(-¥, )∪( ,+¥).
8.(北师大版第54页B组第5题)恒成立问题
变式1: 解:(I) 函数 f (x) 的定义域为 R,即不等式a x 2 + 2x + 1 > 0 的解集为 R,
∴应有 Þ a > 1,
∴ 实数 a 的取值范围是(1,+¥) .
(II) 函数 f (x) 的值域为 R,即a x 2 + 2x + 1 能够取 (0,+¥) 的所有值.
1° 当 a = 0 时,a x 2 + 2x + 1 = 2x + 1满足要求;
2° 当 a ≠ 0 时,应有 Þ 0 < a≤1.
∴ 实数 a 的取值范围是[0,1] .
变式2: 解法一:(转化为最值)
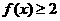 在
在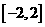 上恒成立,即
上恒成立,即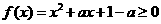 在
在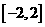 上恒成立.
上恒成立.
⑴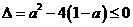 ,
, 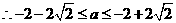 ;
;
⑵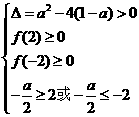 ,
,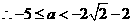 .
.
综上所述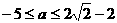 .
.
解法二:(运用根的分布)
⑴当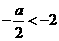 ,即
,即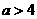 时,应有
时,应有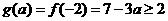 , 即
, 即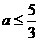 ,
,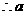 不存在;
不存在;
⑵当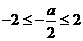 ,即
,即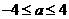 时,应有
时,应有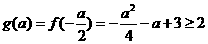 ,
,
即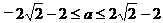 ,
,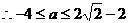 ;
;
⑶当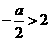 ,即
,即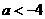 时,应有
时,应有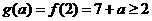 ,即
,即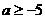 ,
, 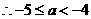
综上所述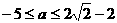 .
.
变式3: 证明:(I) 依题意,f (sin ) = f (1)≥0,f (2 + cos p) = f (1)≤0,
∴ f (1) = 0 Þ 1 + b + c = 0 Þ b + c = -1,
(II) 由 (I) 得: f (x) = x 2-(c + 1) x + c (*)
∵ f (2 + cos b )≤0 Þ (2 + cos b ) 2-(c + 1) (2 + cos b ) + c≤0
Þ (1 + cos b ) [c-(2 + cos b )]≥0,对任意 b 成立.
∵ 1 + cos b ≥0 Þ c≥2 + cos b ,
∴ c≥(2 + cos b )max = 3.
(III) 由 (*) 得:f (sin a ) = sin 2a-(c + 1) sin a + c,
设 t = sin a ,则g(t) = f (sin a ) = t 2-(c + 1) t + c,-1≤t≤1,
这是一开口向上的抛物线,对称轴为 t = ,
由 (II) 知:t≥= 2,
∴ g(t) 在 [-1,1] 上为减函数.
∴ g(t)max = g(-1) = 1 + (c + 1) + c = 2c + 2 = 8,
∴ c = 3
∴ b = -c-1 = -4.
7.(北师大版第54页A组第6题)值域
变式1: 解:作出函数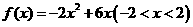 的图象,容易发现在
的图象,容易发现在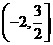 上是增函数,在
上是增函数,在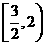 上是减函数,求出
上是减函数,求出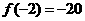 ,
,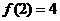 ,
,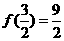 ,注意到函数定义不包含
,注意到函数定义不包含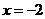 ,所以函数值域是
,所以函数值域是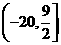 .
.
变式2:解:∵ y= cos2x+sinx=-2sin2x+sinx+1,令t= sinx Î [-1,1],
则y=-2t2+t+1,其中tÎ [-1,1],
∴y Î [-2, ],即原函数的值域是[-2, ].
变式3: 解:(I) ∵ f (1 + x) = f (1-x),
∴ - = 1,
又方程 f (x) = x 有等根 Û a x 2 + (b-1) x = 0 有等根,
∴ △= (b-1) 2 = 0 Þ b = 1 Þ a = -,
∴ f (x) = -x 2 + x.
(II) ∵ f (x) 为开口向下的抛物线,对称轴为 x = 1,
1° 当 m≥1 时,f (x) 在 [m,n] 上是减函数,
∴ 3m = f (x)min = f (n) = -n 2 + n (*),
3n = f (x)max = f (m) = -m 2 + m,
两式相减得:3 (m-n) = -(n 2-m 2) + (n-m),
∵ 1≤m < n,上式除以 m-n 得:m + n = 8,
代入 (*) 化简得:n 2-8n + 48 = 0 无实数解.
2° 当 n≤1 时,f (x) 在 [m,n] 上是增函数,
∴ 3m = f (x)min = f (m) = -m 2 + m,
3n = f (x)max = f (n) = -n 2 + n,
∴ m = -4,n = 0.
3° 当 m≤1≤n 时,对称轴 x = 1 Î [m,n],
∴ 3n = f (x)max = f (1) = Þ n = 与 n≥1 矛盾.
综合上述知,存在 m = -4、n = 0 满足条件.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com