
题目列表(包括答案和解析)
2.若函数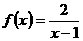 的定义域是
的定义域是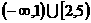 ,则其值域为
( )
,则其值域为
( )
A.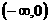 B.
B.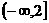 C.
C.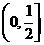 D.
D.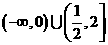

1.已知集合 ={
={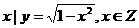 },
}, 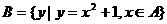 ,则
,则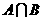 为 ( )
为 ( )
A.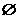 B.
B.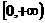 C.{1} D.{(
C.{1} D.{(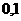 )}
)}
22.(1)证明:.设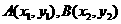 有
有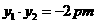 ,下证之:
,下证之:
设直线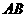 的方程为:
的方程为: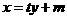 与
与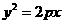 联立得
联立得
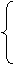
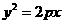
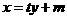
消去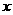 得
得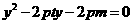
由韦达定理得
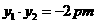 ,
,
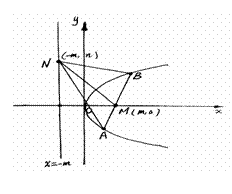 (2)解:三条直线
(2)解:三条直线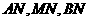 的斜率成等差数列,下证之:
的斜率成等差数列,下证之:
设点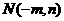 ,则直线
,则直线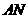 的斜率为
的斜率为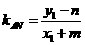 ;
;
直线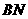 的斜率为
的斜率为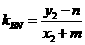
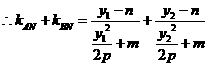
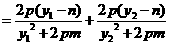
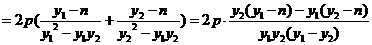
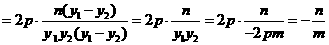
又 直线
直线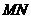 的斜率为
的斜率为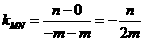
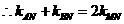
即直线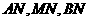 的斜率成等差数列.
的斜率成等差数列.
21.解(1)∵函数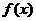 图象关于原点对称,∴对任意实数
图象关于原点对称,∴对任意实数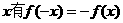 ,
,
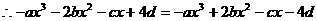 ,即
,即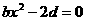 恒成立
恒成立
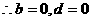
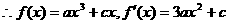 ,
,
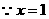 时,
时,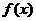 取极小值
取极小值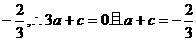 ,解得
,解得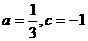
(2)当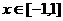 时,图象上不存在这样的两点使结论成立.
时,图象上不存在这样的两点使结论成立.
假设图象上存在两点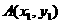 、
、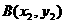 ,使得过此两点处的切线互相垂直,
,使得过此两点处的切线互相垂直,
则由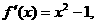 知两点处的切线斜率分别为
知两点处的切线斜率分别为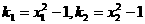 ,
,
且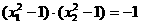 ( *)
( *)
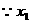 、
、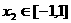 ,
,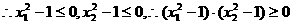
此与(*)相矛盾,故假设不成立.
证明(3)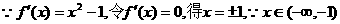 ,
,
或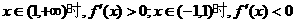 ,
,
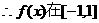 上是减函数,且
上是减函数,且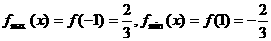
∴在[-1,1]上, 时,
时,
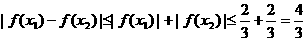 .
.
20. 解:(1)延长B1E交BC于F,
∵ΔB1EC∽ΔFEB, BE=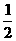 EC1
EC1
∴BF=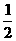 B1C1=
B1C1=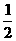 BC,从而F为BC的中点.
BC,从而F为BC的中点.
∵G为ΔABC的重心,∴A、G、F三点共线,且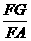 =
= 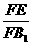 =
=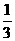 ,∴GE∥AB1,
,∴GE∥AB1,
又GE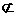 侧面AA1B1B,
∴GE∥侧面AA1B1B
侧面AA1B1B,
∴GE∥侧面AA1B1B
(2)在侧面AA1B1B内,过B1作B1H⊥AB,垂足为H,∵侧面AA1B1B⊥底面ABC,
∴B1H⊥底面ABC.又侧棱AA1与底面ABC成600的角, AA1= 2,
∴∠B1BH=600,BH=1,B1H=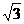 .
.
在底面ABC内,过H作HT⊥AF,垂足为T,连B1T.由三垂线定理有B1T⊥AF,
又平面B1GE与底面ABC的交线为AF,∴∠B1TH为所求二面角的平面角.
∴AH=AB+BH=3,∠HAT=300, ∴HT=AHsin300=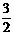 ,
,
在RtΔB1HT中,tan∠B1TH=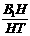 =
=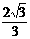 ,
,
从而平面B1GE与底面ABC所成锐二面角的大小为arctan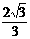
19. (文科做)
解:(1) 第一小组做了三次实验,至少两次实验成功的概率是
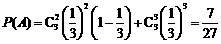 .
.
(2) 第二小组在第4次成功前,共进行了6次试验,其中三次成功三次失败,且恰有两次连续失败,其各种可能的情况种数为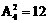 .因此所求的概率为
.因此所求的概率为
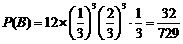 .
.
(理科做)
解:(I)分别记“客人游览甲景点”,“客人游览乙景点”,“客人游览丙景点”
为事件A1,A2,A3. 由已知A1,A2,A3相互独立,P(A1)=0.4,P(A2)=0.5,P(A3)=0.6.
客人游览的景点数的可能取值为0,1,2,3. 相应地,客人没有游览的景点数的可能取值为3,2,1,0,所以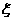 的可能取值为1,3.
的可能取值为1,3.
P(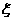 =3)=P(A1·A2·A3)+ P(
=3)=P(A1·A2·A3)+ P(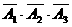 )
)
= P(A1)P(A2)P(A3)+P(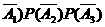 )
)
=2×0.4×0.5×0.6=0.24,
|
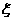 =1)=1-0.24=0.76.
=1)=1-0.24=0.76.
所以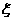 的分布列为
的分布列为
E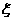 =1×0.76+3×0.24=1.48.
=1×0.76+3×0.24=1.48.
(Ⅱ)解法一 因为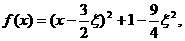
所以函数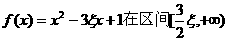 上单调递增,
上单调递增,
要使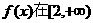 上单调递增,当且仅当
上单调递增,当且仅当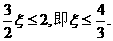
从而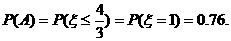
解法二: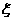 的可能取值为1,3.
的可能取值为1,3.
当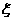 =1时,函数
=1时,函数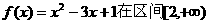 上单调递增,
上单调递增,
当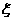 =3时,函数
=3时,函数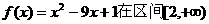 上不单调递增,
上不单调递增,
所以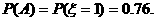
18. 解:(Ⅰ)由已知数据,易知函数y=f(t)的周期T=12,振幅A=3, b=10
∴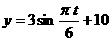 (0≤t≤24)
(0≤t≤24)
(Ⅱ)由题意,该船进出港时,水深应不小于5+6.5=11.5(米)
∴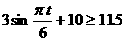
∴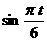
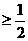 解得,
解得,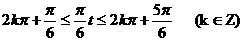
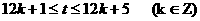
在同一天内,取k=0或1
∴1≤t≤5或13≤t≤17
∴该船最早能在凌晨1时进港,下午17时出港,在港口内最多停留16个小时。
17. 解: (1) 故函数的定义域是(-1,1)
故函数的定义域是(-1,1)
(2)由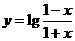 ,得
,得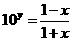 (
(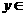 R),所以
R),所以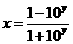 ,
,
所求反函数为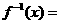
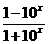 (
( R).
R).
(3) 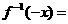
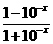 =
=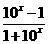 =-
=-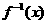 ,所以
,所以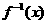 是奇函数.
是奇函数.
16.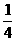
提示:

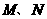 两点,关于直线
两点,关于直线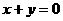 对称,
对称,
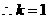 ,又圆心
,又圆心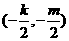 在直线
在直线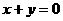 上
上
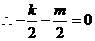
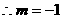
 原不等式组变为
原不等式组变为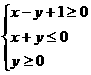 作出不等式组表示的平面区域并计算得面积为
作出不等式组表示的平面区域并计算得面积为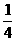 .
.
15.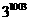
提示:设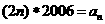 则
则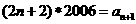 且
且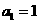
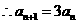
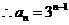 , 即
, 即 ,
,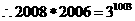
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com