
题目列表(包括答案和解析)
4.已知适合不等式|x2-4x+p|+|x-3|≤5的x的最大值为3.
(1)求p的值;
(2)若f(x)=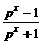 ,解关于x的不等式f--1(x)>
,解关于x的不等式f--1(x)>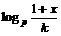 (k∈R+)
(k∈R+)
3.已知关于x的方程sin2x+2cosx+a=0有解,则a的取值范围是__________.
2.已知f(x)、g(x)都是奇函数,f(x)>0的解集是(a2,b),g(x)>0的解集是(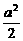 ,
,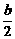 ),则f(x)·g(x)>0的解集是__________.
),则f(x)·g(x)>0的解集是__________.
1.设函数f(x)=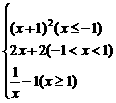 ,已知f(a)>1,则a的取值范围是( )
,已知f(a)>1,则a的取值范围是( )
A.(-∞,-2)∪(-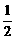 ,+∞) B.(-
,+∞) B.(-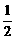 ,
,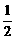 )
)
C.(-∞,-2)∪(-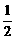 ,1) D.(-2,-
,1) D.(-2,-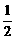 )∪(1,+∞)
)∪(1,+∞)
22.解不等式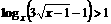
解:由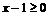 且
且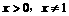 ,得
,得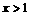 ,
,
原不等式等价于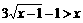
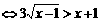 而
而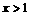 ;
;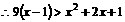
整理,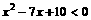
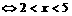
∴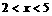 为所求。
为所求。
[不等式的解法练习2]
21、已知函数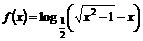 (1)求函数
(1)求函数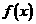 的定义域;(2)判断
的定义域;(2)判断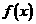 的单调性,并用函数单调性的定义予以证明
的单调性,并用函数单调性的定义予以证明
解:(1)由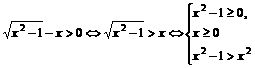 或
或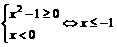 ,
,
故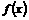 的定义域为
的定义域为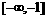
(2)任取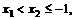 令
令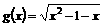 ,则
,则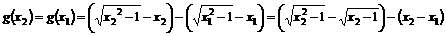
=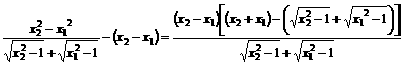
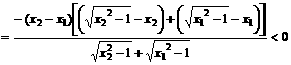 ,
,
故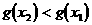 又函数
又函数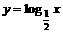 在
在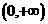 上是减函数,
上是减函数,
所以有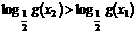 ,即
,即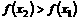
 ,
,
即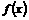 在
在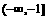 上是增函数
上是增函数
20.对于x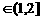 ,关于x的不等式
,关于x的不等式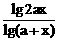 <1总成立,求实数a的取值范围。
<1总成立,求实数a的取值范围。
解:由1<x≤2,得a>0,a+x>1,∴lg(a+x)>0 ∴有lg2ax<lg(a+x),2ax<a+x (2a-1)x<a
(1)a>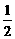 时,x<
时,x<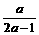 ,由1<x≤2时x<
,由1<x≤2时x<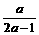 总成立,得
总成立,得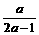 >2,∴
>2,∴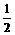 <a<
<a<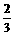
(2)a=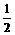 时,有0·x<
时,有0·x<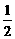 ∴1<x≤2时不等式总成立
∴1<x≤2时不等式总成立
(3)0<a<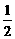 时,x>
时,x>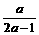 ,由1<x≤2时x>
,由1<x≤2时x>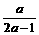 总成立,得a≤1,综合0<a<
总成立,得a≤1,综合0<a<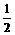 ,得0<a<
,得0<a<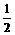
综上,0<a<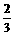
19. 解不等式: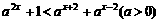
解:∵ a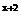 +a
+a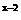 =(a2+
=(a2+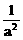 )ax,变形原不等式,得
)ax,变形原不等式,得
a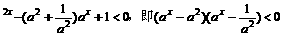
(1) 当0 < a < 1时,a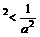 ,则a2 < ax
< a-2,∵-2 < x < 2
,则a2 < ax
< a-2,∵-2 < x < 2
(2) 当a>1时,a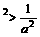 ,则a-2 < ax
< a2,∴-2<x<2
,则a-2 < ax
< a2,∴-2<x<2
(3) 当a=1时,a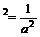 ,无解。 综上,当a≠1时,-2 < x < 2,当a=1时无解。
,无解。 综上,当a≠1时,-2 < x < 2,当a=1时无解。
18.关于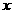 的不等式
的不等式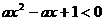 的解集是空集,那么
的解集是空集,那么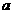 的取值区间是 [0,4]
的取值区间是 [0,4]
17.不等式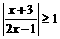 的解集是
的解集是 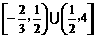
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com