
题目列表(包括答案和解析)
5.已知cos(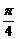 +x)=
+x)=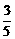 ,(
,(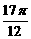 <x<
<x<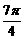 ),求
),求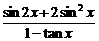 的值.
的值.
4.不查表求值: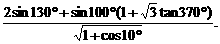
3.设α∈( ),β∈(0,
),β∈(0,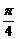 ),cos(α-
),cos(α-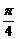 )=
)=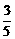 ,sin(
,sin(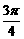 +β)=
+β)=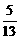 ,则sin(α+β)=_________.
,则sin(α+β)=_________.
2.已知sinα=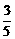 ,α∈(
,α∈(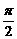 ,π),tan(π-β)=
,π),tan(π-β)=  ,则tan(α-2β)=_________.
,则tan(α-2β)=_________.
1.已知方程x2+4ax+3a+1=0(a>1)的两根均tanα、tanβ,且α,β∈
(-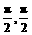 ),则tan
),则tan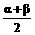 的值是( )
的值是( )
A. B.-2 C.
B.-2 C.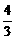 D.
D.
 或-2
或-2
[两角和与差的三角函数练习1]
两角和与差的三角函数
[例1]
已知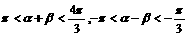 ,求
,求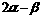 的范围。
的范围。
解:设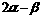 =
=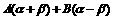 ,(A、B为待定的系数),则
,(A、B为待定的系数),则
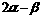 =
=
比较系数 ∴
∴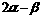 =
=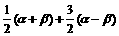
从而可得: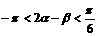
[例2]
设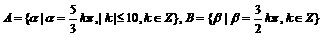 ,求
,求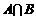 的解的终边相同的角的集合。
的解的终边相同的角的集合。
解:先写出A与B的交,再写出终边相同的角的集合。
设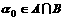 ,则
,则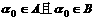 ;所以
;所以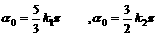
∴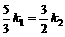 ,即
,即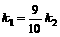 ,由于
,由于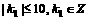
∴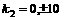 ;因此
;因此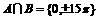
因此所有与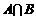 的角的终边相同的角的集合为
的角的终边相同的角的集合为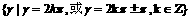
[例3]
已知 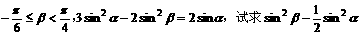 的最值。
的最值。
解:∵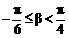 ∴-
∴-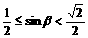 ,
,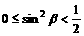 ∴
∴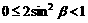
∵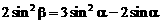 ∴
∴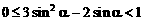
即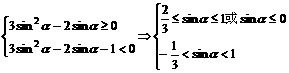
∴ 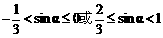
y=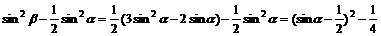
当sina∈[ ,1]时函数y递增,∴当sina=
,1]时函数y递增,∴当sina=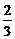 时 ymin=
时 ymin=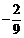 ;
;
当sina∈(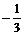 ,0)时,函数y递减,∴当sina=0时,ymin=
,0)时,函数y递减,∴当sina=0时,ymin=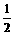
∴ 故当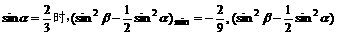 无最大值。
无最大值。
[例4]
求值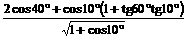
解:
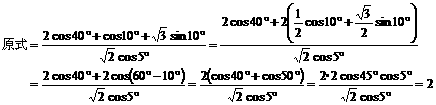
[例5]
已知 <β<α<
<β<α<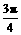 ,cos(α-β)=
,cos(α-β)=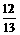 ,sin(α+β)=-
,sin(α+β)=- ,求sin2α的值_________.
,求sin2α的值_________.
解法一:∵ <β<α<
<β<α<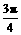 ,∴0<α-β<
,∴0<α-β<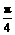 .π<α+β<
.π<α+β<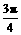 ,
,
∴sin(α-β)=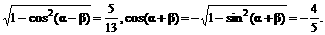
∴sin2α=sin[(α-β)+(α+β)]
=sin(α-β)cos(α+β)+cos(α-β)sin(α+β)
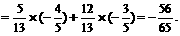
解法二:∵sin(α-β)=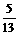 ,cos(α+β)=-
,cos(α+β)=-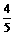 ,
,
∴sin2α+sin2β=2sin(α+β)cos(α-β)=-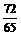
sin2α-sin2β=2cos(α+β)sin(α-β)=-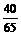
∴sin2α=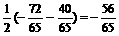
[例6]
不查表求sin220°+cos280°+ cos20°cos80°的值.
cos20°cos80°的值.
解法一:sin220°+cos280°+ sin220°cos80°
sin220°cos80°
= (1-cos40°)+
(1-cos40°)+ (1+cos160°)+
(1+cos160°)+  sin20°cos80°
sin20°cos80°
=1- cos40°+
cos40°+ cos160°+
cos160°+ sin20°cos(60°+20°)
sin20°cos(60°+20°)
=1- cos40°+
cos40°+ (cos120°cos40°-sin120°sin40°)
(cos120°cos40°-sin120°sin40°)
+ sin20°(cos60°cos20°-sin60°sin20°)
sin20°(cos60°cos20°-sin60°sin20°)
=1- cos40°-
cos40°-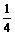 cos40°-
cos40°-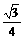 sin40°+
sin40°+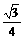 sin40°-
sin40°-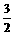 sin220°
sin220°
=1-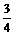 cos40°-
cos40°-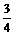 (1-cos40°)=
(1-cos40°)=
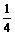
解法二:设x=sin220°+cos280°+ sin20°cos80°
sin20°cos80°
y=cos220°+sin280°- cos20°sin80°,则
cos20°sin80°,则
x+y=1+1- sin60°=
sin60°= ,x-y=-cos40°+cos160°+
,x-y=-cos40°+cos160°+ sin100°
sin100°
=-2sin100°sin60°+ sin100°=0
sin100°=0
∴x=y=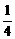 ,即x=sin220°+cos280°+
,即x=sin220°+cos280°+ sin20°cos80°=
sin20°cos80°=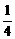 .
.
[例7]
设关于x的函数y=2cos2x-2acosx-(2a+1)的最小值为f(a),试确定满足f(a)=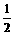 的a值,并对此时的a值求y的最大值.
的a值,并对此时的a值求y的最大值.
解:由y=2(cosx-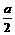 )2-
)2-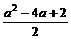 及cosx∈[-1,1]得:
及cosx∈[-1,1]得:
f(a)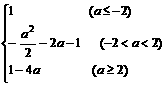
∵f(a)= ,∴1-4a=
,∴1-4a=
 a=
a=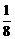
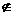 [2,+∞
[2,+∞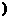
故-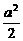 -2a-1=
-2a-1= ,解得:a=-1,此时,
,解得:a=-1,此时,
y=2(cosx+ )2+
)2+ ,当cosx=1时,即x=2kπ,k∈Z,ymax=5.
,当cosx=1时,即x=2kπ,k∈Z,ymax=5.
[例8]
求值: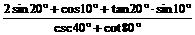 .
.
解:原式的分子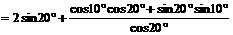
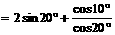
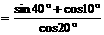
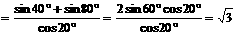 ,
,
原式的分母=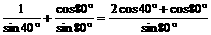
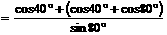
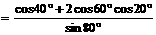
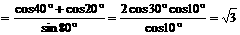 ,
,
所以,原式=1.
[例9]
已知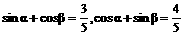 ,求
,求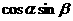 的值.
的值.
解1:令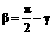 ,则原题等价于:
,则原题等价于:
已知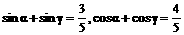 ,求
,求 的值.
的值.
两式分别和差化积并相除得: ,所以
,所以
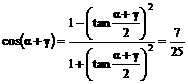 .
.
分别将已知两式平方并求和得: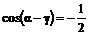 ,
,
所以,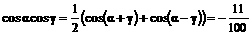 .
.
解2:由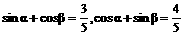 平方相加得:
平方相加得: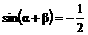 .
.
上述两式平方相减得: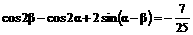 .
.
将上式前两项和差化积,得: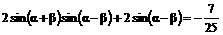 ,
,
结合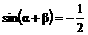 ,可解得:
,可解得: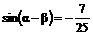 .
.
所以,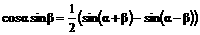
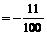 .
.
[例10]
已知函数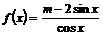 在区间
在区间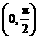 上单调递减,试求实数
上单调递减,试求实数 的取值范围.
的取值范围.
解:已知条件实际上给出了一个在区间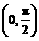 上恒成立的不等式.
上恒成立的不等式.
任取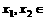
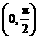 ,且
,且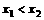 ,则不等式
,则不等式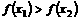 恒成立,
恒成立,
即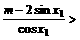
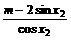 恒成立.
恒成立.
化简得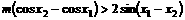
由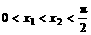 可知:
可知: ,
,
所以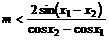
上式恒成立的条件为: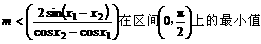 .
.
由于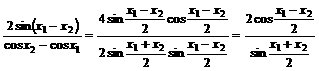
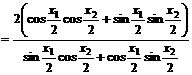
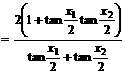
且当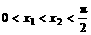 时,
时,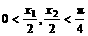 ,所以
,所以 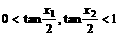 ,
,
从而 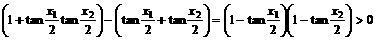 ,
,
有 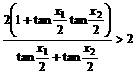 ,
,
故 的取值范围为
的取值范围为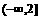 .
.
[例11]
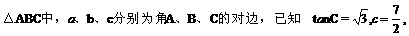
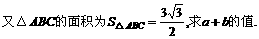
解:∵ A+B+C=π,
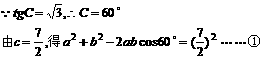
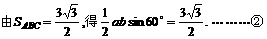
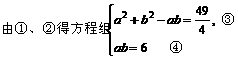
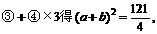

[例12]
在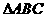 中,
中,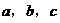 分别是角
分别是角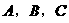 的对边,设
的对边,设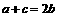 ,求
,求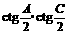 的值
的值
解:由条件,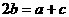 ,依据正弦定理,得
,依据正弦定理,得
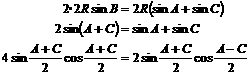
在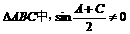
∴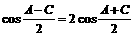
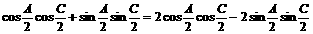
∴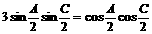
∴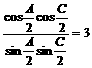 ; 即
; 即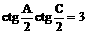
三角函数的图象与性质
[例1] 试确定下列函数的定义域
⑴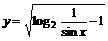 ;⑵
;⑵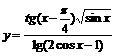
解:⑴要使函数有意义,只须满足条件
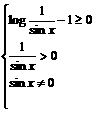 解得:
解得: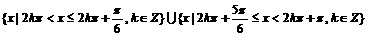
⑵要使函数有意义,只须满足条件
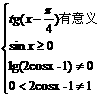 解得
解得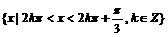
[例2]
求函数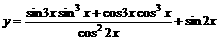 的最小值
的最小值
解:∵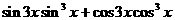
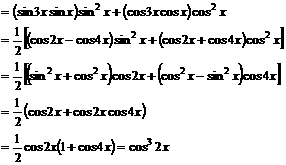
∴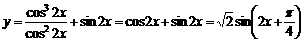
当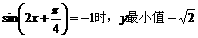
[例3]
已知函数f(x)=2asin2x-2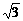 asinxcosx+a+b-1,(a、b为常数,a<0),它的定义域为[0,
asinxcosx+a+b-1,(a、b为常数,a<0),它的定义域为[0,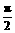 ],值域为[-3,1],试求a、b的值。
],值域为[-3,1],试求a、b的值。
解:f(x)=2asin2x-2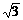 asinxcosx+a+b-1
asinxcosx+a+b-1
=a(1-cos2x)-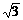 asin2x+a+b-1
asin2x+a+b-1
=-2asin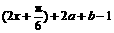
∵0≤x≤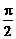 ∴
∴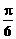 ≤2x+
≤2x+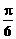 ≤
≤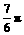 ∴
∴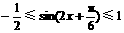
∵a<0 ∴a≤-2asin -2a
-2a
∴3a+b-1≤-2asin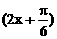 +2a+b-1≤b-1
+2a+b-1≤b-1
∵值域为[-3,1] ∴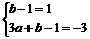 ∴
∴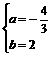
[例4]
已知函数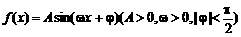 的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(
的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(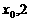 )和(
)和(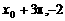 ).
).
(1)求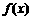 的解析式;
的解析式;
(2)将y=f(x)图象上所有点的横坐标缩短到原来的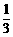 (纵坐标不变),然后再将所得图象向x轴正方向平移
(纵坐标不变),然后再将所得图象向x轴正方向平移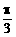 个单位,得到函数y=g(x)的图象.写出函数y=g(x)的解析式并用列表作图的方法画出y=g(x)在长度为一个周期的闭区间上的图象.
个单位,得到函数y=g(x)的图象.写出函数y=g(x)的解析式并用列表作图的方法画出y=g(x)在长度为一个周期的闭区间上的图象.
解:(1)由已知,易得A=2.
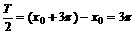 ,解得
,解得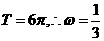 .
.
把(0,1)代入解析式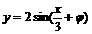 ,得
,得
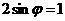 .又
.又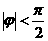 ,解得
,解得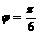 .∴
.∴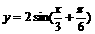 为所求.
为所求.
(2)压缩后的函数解析式为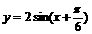 再平移,
再平移,
得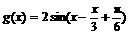
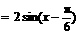
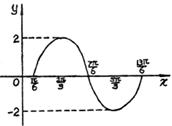
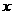
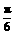
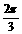
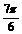
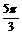
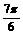
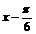
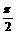
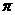

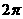
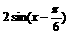
[例5]
求函数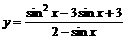 的最值,并写出使函数
的最值,并写出使函数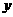 取得最值的
取得最值的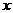 的集合。
的集合。
解:令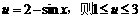 ,
,
∴函数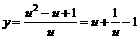
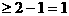
当且仅当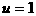 时,
时,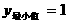
函数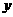 取得最小值的
取得最小值的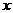 的集合
的集合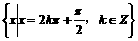
又函数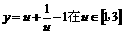 是单调递增的
是单调递增的
证明如下: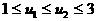
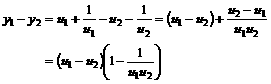
∵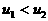 ∴
∴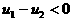
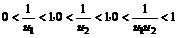
∴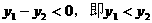 ,∴
,∴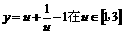 是单调递增的
是单调递增的
∴当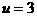 时,函数
时,函数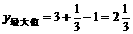
函数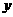 取得最大值的
取得最大值的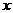 的集合
的集合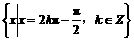
[例6]
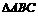 中,已知三内角A、B、C依次成等差数列,求
中,已知三内角A、B、C依次成等差数列,求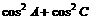 的取值范围。
的取值范围。
解:由已知得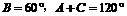
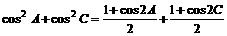
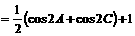
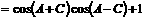
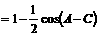
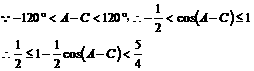
即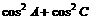 的取值范围为
的取值范围为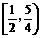
[例7]
已知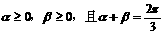 ,问当
,问当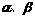 分别取何值时,
分别取何值时,
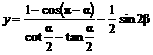 取最大值,并求出此最大值。
取最大值,并求出此最大值。
解: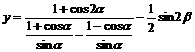
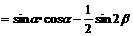
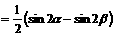
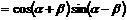
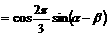
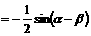
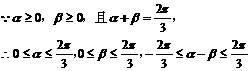
此时,由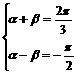 解得
解得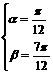
[例8]
在ΔABC中,求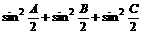 的最小值.并指出取最小值时ΔABC的形状,并说明理由.
的最小值.并指出取最小值时ΔABC的形状,并说明理由.
解:令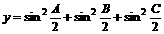
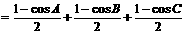
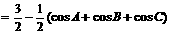
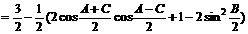
∵在ΔABC中,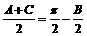 ,∴
,∴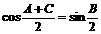
又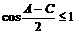 .
.
∴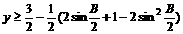
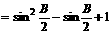
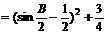
当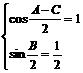 时,y取得最小值
时,y取得最小值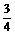 ;
;
由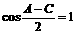 知A=C,由
知A=C,由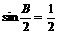 知
知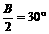 ,B=60°;
,B=60°;
故A=B=C=60°,
即y取最小值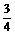 时,ΔABC的形状为等边三角形.
时,ΔABC的形状为等边三角形.
[例9]
已知函数f(x)=2cosxsin(x+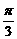 )-
)- sin2x+sinxcosx
sin2x+sinxcosx
(1)求函数f(x)的最小正周期;
(2)求f(x)的最小值及取得最小值时相应的x的值;
(3)若当x∈[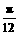 ,
,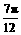 ]时,f(x)的反函数为f-1(x),求f--1(1)的值.
]时,f(x)的反函数为f-1(x),求f--1(1)的值.
解:(1)f(x)=2cosxsin(x+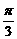 )-
)- sin2x+sinxcosx
sin2x+sinxcosx
=2cosx(sinxcos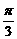 +cosxsin
+cosxsin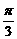 )-
)- sin2x+sinxcosx
sin2x+sinxcosx
=2sinxcosx+ cos2x=2sin(2x+
cos2x=2sin(2x+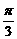 )
)
∴f(x)的最小正周期T=π
(2)当2x+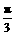 =2kπ-
=2kπ-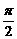 ,即x=kπ-
,即x=kπ-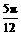 (k∈Z)时,f(x)取得最小值-2.
(k∈Z)时,f(x)取得最小值-2.
(3)令2sin(2x+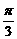 )=1,又x∈[
)=1,又x∈[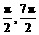 ],
],
∴2x+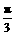 ∈[
∈[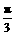 ,
,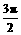 ],∴2x+
],∴2x+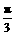 =
=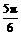 ,则
,则
x=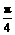 ,故f--1(1)=
,故f--1(1)=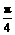 .
.
[例10]
已知α、β为锐角,且x(α+β-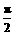 )>0,试证不等式f(x)=
)>0,试证不等式f(x)=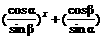 x<2对一切非零实数都成立.
x<2对一切非零实数都成立.
证明:若x>0,则α+β>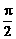 ,
,
∵α、β为锐角,∴0< -α<β<
-α<β< ;0<
;0< -β<
-β< ,
,
∴0<sin( -α)<sinβ.0<sin(
-α)<sinβ.0<sin(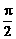 -β)<sinα,
-β)<sinα,
∴0<cosα<sinβ,0<cosβ<sinα,
∴0<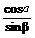 <1,0<
<1,0<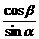 <1,
<1,
∴f(x)在(0,+∞)上单调递减,∴f(x)<f(0)=2.
若x<0,α+β< ,
,
∵α、β为锐角,0<β< -α<
-α< ,0<α<
,0<α< -β<
-β< ,0<sinβ<sin(
,0<sinβ<sin(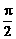 -α),
-α),
∴sinβ<cosα,0<sinα<sin( -β),∴sinα<cosβ,∴
-β),∴sinα<cosβ,∴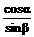 >1,
>1, 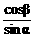 >1,
>1,
∵f(x)在(-∞,0)上单调递增,∴f(x)<f(0)=2,∴结论成立.
[例11] 设z1=m+(2-m2)i,z2=cosθ+(λ+sinθ)i,其中m,λ,θ∈R,已知z1=2z2,求λ的取值范围.
解法一:∵z1=2z2,
∴m+(2-m2)i=2cosθ+(2λ+2sinθ)i,∴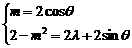
∴λ=1-2cos2θ-sinθ=2sin2θ-sinθ-1=2(sinθ-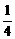 )2-
)2-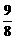 .
.
当sinθ=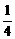 时λ取最小值-
时λ取最小值-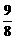 ,当sinθ=-1时,λ取最大值2.
,当sinθ=-1时,λ取最大值2.
解法二:∵z1=2z2 ∴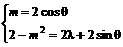
∴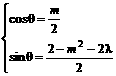 ,
,
∴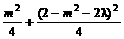 =1.
=1.
∴m4-(3-4λ)m2+4λ2-8λ=0,设t=m2,则0≤t≤4,
令f(t)=t2-(3-4λ)t+4λ2-8λ,则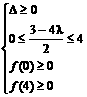 或f(0)·f(4)≤0
或f(0)·f(4)≤0
∴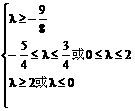
∴-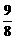 ≤λ≤0或0≤λ≤2.
≤λ≤0或0≤λ≤2.
∴λ的取值范围是[-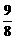 ,2].
,2].
[例12]
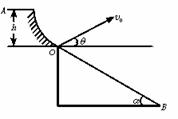 如右图,一滑雪运动员自h=50m高处A点滑至O点,由于运动员的技巧(不计阻力),在O点保持速率v0不为,并以倾角θ起跳,落至B点,令OB=L,试问,α=30°时,L的最大值为多少?当L取最大值时,θ为多大?
如右图,一滑雪运动员自h=50m高处A点滑至O点,由于运动员的技巧(不计阻力),在O点保持速率v0不为,并以倾角θ起跳,落至B点,令OB=L,试问,α=30°时,L的最大值为多少?当L取最大值时,θ为多大?
解:由已知条件列出从O点飞出后的运动方程:
|
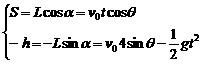
由①②整理得:v0cosθ=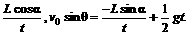
∴v02+gLsinα=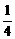 g2t2+
g2t2+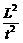 ≥
≥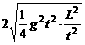 =gL
=gL
运动员从A点滑至O点,机械守恒有:mgh= mv02,
mv02,
∴v02=2gh,∴L≤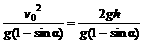 =200(m)
=200(m)
即Lmax=200(m),又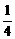 g2t2=
g2t2=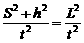 .
.
∴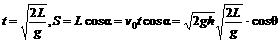
得cosθ=cosα,∴θ=α=30°∴L最大值为200米,当L最大时,起跳仰角为30°.
[例13] 如下图,某地一天从6时到14时的温度变化曲线近似满足函数:
y=Asin(ωx+φ)+b;(1)求这段时间的最大温差;(2)写出这段曲线的函数解析式.
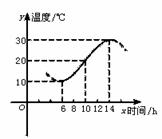
解:(1)由图示,这段时间的最大温差是30-10=20(℃);
(2)图中从6时到14时的图象是函数y=Asin(ωx+φ)+b的半个周期的图象.
∴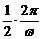 =14-6,解得ω=
=14-6,解得ω=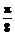 ,由图示A=
,由图示A= (30-10)=10,b=
(30-10)=10,b= (30+10)=20,这时y=10sin(
(30+10)=20,这时y=10sin(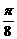 x+φ)+20,将x=6,y=10代入上式可取φ=
x+φ)+20,将x=6,y=10代入上式可取φ=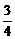 π.综上所求的解析式为y=10sin(
π.综上所求的解析式为y=10sin(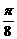 x+
x+
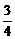 π)+20,x∈[6,14].
π)+20,x∈[6,14].
[例14]
已知函数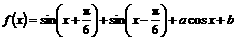 (
(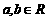 ,且均为常数),
,且均为常数),
(1)求函数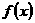 的最小正周期;
的最小正周期;
(2)若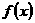 在区间
在区间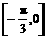 上单调递增,且恰好能够取到
上单调递增,且恰好能够取到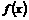 的最小值2,试求
的最小值2,试求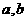 的值.
的值.
解:研究三角函数的性质(如周期、最值、单调性、奇偶性等)时,首先应该对所给的函数关系式进行化简,最好化为一个角(形如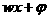 )、一种三角函数的形式.
)、一种三角函数的形式.
(1) 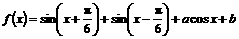
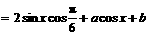
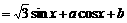
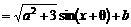
(其中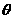 由下面的两式所确定:
由下面的两式所确定: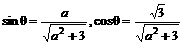 )
)
所以,函数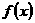 的最小正周期为
的最小正周期为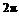 .
.
(2) 由(1)可知: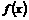 的最小值为
的最小值为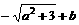 ,所以,
,所以,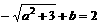 .
.
另外,由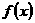 在区间
在区间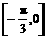 上单调递增,可知:
上单调递增,可知: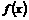 在区间
在区间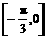 上的最小值为
上的最小值为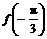 ,所以,
,所以,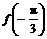 =
=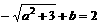 .
.
解之得: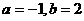
[例15]
设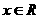 ,试比较
,试比较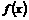 =
= 与
与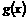 =
=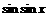 的大小关系.
的大小关系.
解:观察所给的两个函数,它们均是两个三角函数的复合函数,因此,我们不难想到:它们可能仍然具备三角函数的某些性质,如单调性、周期性、奇偶性等.
初步判断便可以确定: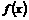 、
、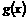 都是周期函数,且最小正周期分别为
都是周期函数,且最小正周期分别为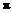 、
、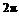 .所以,只需考虑
.所以,只需考虑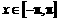 的情形.
的情形.
另外,由于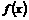 为偶函数,
为偶函数,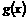 为奇函数,所以,很自然的可以联想到:能否把需考虑的
为奇函数,所以,很自然的可以联想到:能否把需考虑的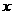 的范围继续缩小?
的范围继续缩小?
事实上,当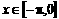 时,
时,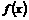 >0,
>0,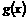
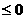 恒成立,此时,
恒成立,此时,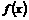 >
>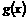 .
.
下面,我们只需考虑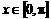 的情形.
的情形.
如果我们把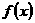 看作是关于
看作是关于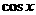 的余弦函数,把
的余弦函数,把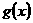 看作是关于
看作是关于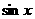 的正弦函数,那么这两个函数既不同名,自变量也不相同,为了能进行比较,我们可以作如下恒等变换,使之成为同名函数,以期利用三角函数的单调性.
的正弦函数,那么这两个函数既不同名,自变量也不相同,为了能进行比较,我们可以作如下恒等变换,使之成为同名函数,以期利用三角函数的单调性.
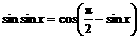
至此为止,可以看出:由于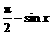 和
和 同属于余弦函数的一个单调区间,(即
同属于余弦函数的一个单调区间,(即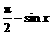 ,
,
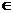
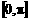 ),所以,只需比较
),所以,只需比较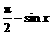 与
与 的大小即可.
的大小即可.
事实上,
(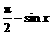 )-
)- =
=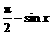 -
- =
=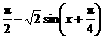
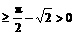
所以,利用余弦函数在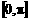 上单调递减,可得:
上单调递减,可得:
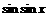 <
< .也即
.也即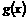 <
<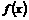
综上,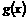 <
<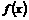 .
.
点评 本题好在充分地运用了正余弦函数的值域、周期性、奇偶性、单调性等性质,对于训练学生思维、加深对这些性质的理解、以及学习利用函数的性质去解决问题有很大的帮助.是一道很有训练价值的好题.
9.在复习中,应立足基本公式,在解题时,注意在条件与结论之间建立联系,在变形过程中不断寻找差异,讲究算理,才能立足基础,发展能力,适应高考.
在本章内容中,高考试题主要反映在以下三方面:其一是考查三角函数的性质及图象变换,尤其是三角函数的最大值与最小值、周期。多数题型为选择题或填空题;其次是三角函数式的恒等变形。如运用三角公式进行化简、求值解决简单的综合题等。除在填空题和选择题出现外,解答题的中档题也经常出现这方面内容。
另外,还要注意利用三角函数解决一些应用问题。
8.注意对三角形中问题的复习.由于教材的变动,有关三角形中的正、余弦定理.解三角形等内容提到高中来学习,又近年加强数形结合思想的考查和对三角变换要求的降低,对三角的综合考查将向三角形中问题伸展,从1996年和1998年的高考试题就可看出,但也不可太难,只要掌握基本知识、概念,深刻理解其中基本的数量关系即可过关.
7.变为主线、抓好训练.变是本章的主题,在三角变换考查中,角的变换,三角函数名的变换,三角函数次数的变换,三角函数式表达形式的变换等比比皆是,在训练中,强化变意识是关键,但题目不可太难,较特殊技巧的题目不做,立足课本,掌握课本中常见问题的解法,把课本中习题进行归类,并进行分析比较,寻找解题规律. 针对高考中题目看,还要强化变角训练,经常注意收集角间关系的观察分析方法.另外如何把一个含有不同名或不同角的三角函数式化为只含有一个三角函数关系式的训练也要加强,这也是高考的重点.同时应掌握三角函数与二次函数相结合的题目.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com