
题目列表(包括答案和解析)
1.理解函数的概念,了解映射的概念.
22.(文科)设集合P=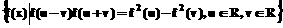
(1)试判断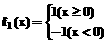 ;
;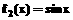 ,是否属于集合P?
,是否属于集合P?
(2)若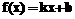
 属于P,试寻找其充要条件.
属于P,试寻找其充要条件.
(3)根据对第(1),(2)小题的研究,请你对属于集合P的函数从函数性质方面提出一个有价值的结论,说明理由;若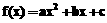
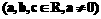 ,利用研究所得的结论判断
,利用研究所得的结论判断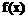 与集合P的关系.
与集合P的关系.
21. (文科)在数列
(文科)在数列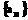 (n
(n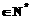 )中,当n为奇数时,
)中,当n为奇数时,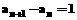 ,当n为偶数时,
,当n为偶数时,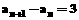 ,且
,且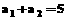 .
.
(1)求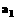 ,
,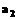 .
.
(2)令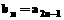 ,(n
,(n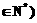 ,判断数列
,判断数列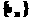 是否为等差数列,并证明你的结论.
是否为等差数列,并证明你的结论.
(3)求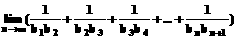 .
.
20. 设A,B分别是双曲线
设A,B分别是双曲线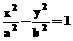
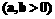 的左右顶点,双曲线的实轴长为
的左右顶点,双曲线的实轴长为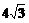 ,焦点到渐近线的距离为
,焦点到渐近线的距离为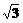 .
.
(1)求此双曲线的方程.
(2)已知直线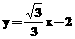 与双曲线的右支交于
与双曲线的右支交于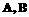 两点,且在双曲线的右支上存在点
两点,且在双曲线的右支上存在点 ,使得
,使得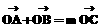 ,求
,求 的值及点
的值及点 的坐标.
的坐标.
19.一长方形泳池中相邻的两条泳道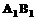 和
和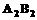 (看成两条互相平行的线段)分别长90米,甲在泳道
(看成两条互相平行的线段)分别长90米,甲在泳道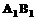 上从
上从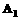 处出发,以3米/秒的速度到达
处出发,以3米/秒的速度到达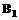 以同样的速度返回
以同样的速度返回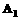 处,然后重复上述过程;乙在泳道
处,然后重复上述过程;乙在泳道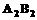 上从
上从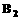 处出发,以2米/秒的速度到达
处出发,以2米/秒的速度到达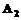 以同样的速度游回
以同样的速度游回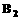 处,然后重复上述过程.(不考虑每次折返时的减速和转向时间).两人同时开始运动.
处,然后重复上述过程.(不考虑每次折返时的减速和转向时间).两人同时开始运动.
 (1)设甲离开池边
(1)设甲离开池边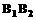 处的距离为y米,当时间
处的距离为y米,当时间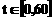 (单位:
(单位:
秒)时,写出y关于t的函数解析式.
(2)在右图的直角坐标系中,x轴表示时间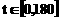 (单位:秒),
(单位:秒),
y轴表示离开池边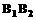 处的距离.在同一个坐标系中画出
处的距离.在同一个坐标系中画出
甲乙两人各自运动的函数图像.(实线表示甲的图像,虚线表示乙的图像).
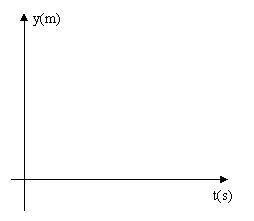 (3)请根据图像判断从开始运动起到3分钟为止,甲乙的相遇次数.
(3)请根据图像判断从开始运动起到3分钟为止,甲乙的相遇次数.

18.已知函数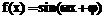 (其中
(其中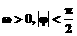 ),
),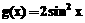 .若函数
.若函数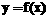 的图像与x轴的任意两个相邻交点间的距离为
的图像与x轴的任意两个相邻交点间的距离为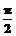 ,且直线
,且直线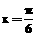 是函数
是函数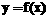 图像的一条对称轴.
图像的一条对称轴.
(1)求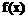 的表达式.
的表达式.
(2)求函数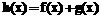 的单调递增区间.
的单调递增区间.
17.设复数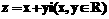 ,且复数
,且复数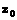 满足
满足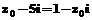 (i为虚数单位),则当
(i为虚数单位),则当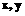 满足什么条件时,
满足什么条件时,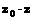 是纯虚数.
是纯虚数.
16.设S是至少含有两个元素的集合.在S上定义了一个二元运算“*”(即对任意的 ,对于有序元素对
,对于有序元素对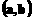 ,在S中有唯一确定的元素
,在S中有唯一确定的元素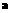 *
*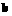 与之对应)。若对任意的
与之对应)。若对任意的 ,有
,有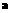 *
*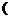
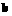 *
*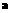
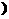 =
=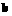 ,则对任意的
,则对任意的 ,下列等式中不恒成立的是
( )
,下列等式中不恒成立的是
( )
(A)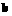 *
*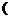
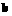 *
*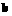
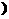 =
=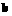 (B)
(B)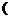
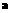 *
*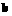
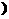 *
*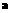 =
=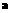
(C)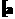 *
*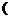
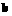 *
*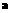
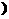
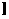 *
*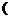
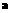 *
*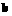
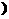 =
=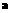 (D)
(D)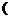
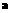 *
*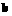
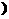 *
*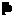 *
*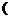
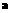 *
*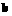
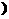
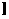 =
=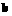

15.已知P是椭圆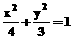 上的点,
上的点,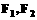 是两个焦点,则
是两个焦点,则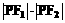 的最大值与最小值之差是
( )
的最大值与最小值之差是
( )
(A)1 (B)2 (C)3 (D)4
14.“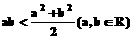 ”是“
”是“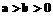 ”的
( )
”的
( )
(A)充分非必要条件 (B)必要非充分条件
(C)充要条件 (D)非充分非必要条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com