
题目列表(包括答案和解析)
20.(本题满分12分)已知函数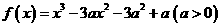
(Ⅰ)求函数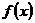 的单调区间;
的单调区间;
(Ⅱ)若曲线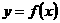 上有两点
上有两点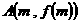 ,
,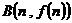 处的切线都与
处的切线都与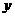 轴垂直,且函数
轴垂直,且函数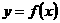 在区间
在区间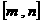 上存在零点,求实数
上存在零点,求实数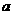 的取值范围.
的取值范围.
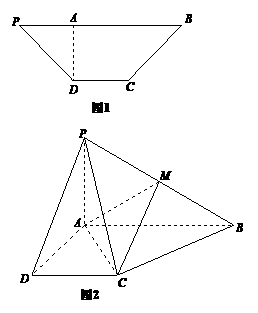
19.(本题满分12分)已知等腰梯形 中(如图1),
中(如图1),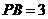 ,
,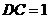 ,
,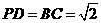 ,
,
 为
为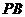 边上一点,且
边上一点,且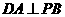 ,现将
,现将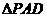 沿
沿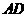 折起,使面
折起,使面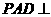 面
面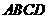 (如图2).
(如图2).
(Ⅰ)证明:平面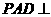 平面
平面 ;
;
(Ⅱ)试在棱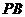 上确定一点
上确定一点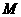 ,使截面
,使截面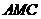 把几何体分成两部分
把几何体分成两部分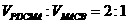 ;
;
(Ⅲ)在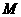 满足(Ⅱ)的情况下,判断直线
满足(Ⅱ)的情况下,判断直线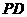 是否平行于平面
是否平行于平面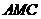 ,并说明理由.
,并说明理由.
18. (本题满分12分) 某化妆品生产企业为了占有更多的市场份额,拟在2008年北京奥运会期间进行一系列促销活动,经过市场调查和测算,化妆品的年销量x万件与年促销费t万元之间满足关系式: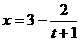 ,已知2008年生产化妆品的设备折旧、维修等固定费用为3万元,每生产1万件化妆品需再投入32万元的生产费用,若化妆品的年销售收入额定为:其年生产成本的150%与年促销费的一半之和.问:该企业2008年的促销费投入多少万元时,企业的年利润
,已知2008年生产化妆品的设备折旧、维修等固定费用为3万元,每生产1万件化妆品需再投入32万元的生产费用,若化妆品的年销售收入额定为:其年生产成本的150%与年促销费的一半之和.问:该企业2008年的促销费投入多少万元时,企业的年利润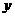 (万元)最大?(注:利润=销售收入-生产成本-促销费,生产成本=固定费用+生产费用)
(万元)最大?(注:利润=销售收入-生产成本-促销费,生产成本=固定费用+生产费用)
17.(本题满分12分)在△ABC中,角A、B、C的对边分别为a、b、c,且满足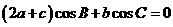 .
.
(Ⅰ)求角B的大小;
|
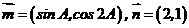 ,当
,当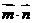 取到最大值时,角
取到最大值时,角 和角
和角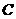 的值.
的值.16.下列四种说法:
①命题“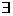 x∈R,使得x2+1>3x”的否定是“
x∈R,使得x2+1>3x”的否定是“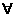 x∈R,都有x2+1≤3x”;
x∈R,都有x2+1≤3x”;
②设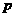 、
、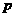 是简单命题,若“
是简单命题,若“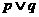 ”为假命题,则“
”为假命题,则“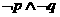 ” 为真命题;
” 为真命题;
③把函数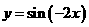
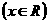 的图像上所有的点向右平移
的图像上所有的点向右平移 个单位即可得到函数
个单位即可得到函数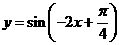
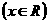 的图像.
的图像.
其中所有正确说法的序号是 .
15.如图是从事网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推.则第99行从左至右算第67个数字为 .
14.下表是某厂1-4月份用水量(单位:百吨)的一组数据,
月份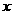 |
1 |
2 |
3 |
4 |
用水量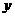 |
4.5 |
4 |
3 |
2.5 |
由其散点图可知,用水量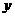 与月份
与月份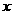 之间有较好的线性相关关系,其线性回归方程是
之间有较好的线性相关关系,其线性回归方程是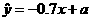 ,则
,则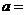 .
.

13.在圆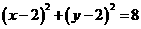 内有一平面区域
内有一平面区域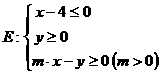 ,点
,点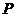 是圆内的任意一点,而且出现任何一个点是等可能的.若使点
是圆内的任意一点,而且出现任何一个点是等可能的.若使点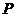 落在该平面区域
落在该平面区域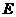 内的概率最大,则
内的概率最大,则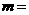 .
.
12.已知数列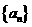 为等差数列,若
为等差数列,若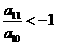 ,且它们的前
,且它们的前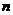 项和
项和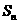 有最大值,则使得
有最大值,则使得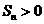 的
的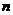 的最大值为 ( )
的最大值为 ( )
A.11 B.19 C. 20 D.21
济宁市2007-2008学年度高三复习第一阶段质量检测
数学试题(文科) 2008.03
第Ⅱ卷(非选择题,共90分)
11.若函数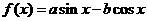
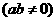 ,对任意的实数
,对任意的实数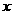 满足
满足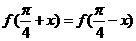 ,则直线
,则直线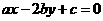 的斜率是( )
的斜率是( )
A.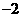 B.2 C.
B.2 C.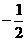 D.
D. 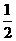
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com