
题目列表(包括答案和解析)
7、解法一:设所求椭圆的直角坐标方程是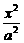 +
+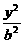 =1,其中a>b>0待定
=1,其中a>b>0待定
由e2=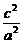 =
=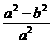 =1-(
=1-(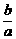 )2
)2
可知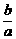 =
=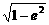 =
=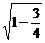 =
=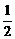 ,即a=2b
,即a=2b
设椭圆上的点(x,y)到点P的距离为d,
则d2=x2+(y-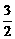 )2=a2(1-
)2=a2(1-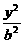 )+y2-3y+
)+y2-3y+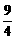
= 4b2-3y2-3y+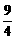 =-3(y+
=-3(y+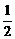 )2+4b2+3,其中-b≤y≤b
)2+4b2+3,其中-b≤y≤b
如果b<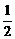 ,则当y=-b时d2(从而d)有最大值,
,则当y=-b时d2(从而d)有最大值,
由题设得(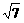 )2=(b+
)2=(b+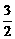 )2,
)2,
由此得b=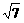 -
-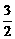 >
>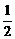 ,与b<
,与b<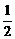 矛盾
矛盾
因此必有b≥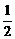 成立,于是当y=-
成立,于是当y=-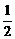 时d2(从而d)有最大值,
时d2(从而d)有最大值,
由题设得(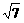 )2=4b2+3,由此可得b=1,a=2
)2=4b2+3,由此可得b=1,a=2
故所求椭圆的直角坐标方程是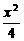 +y2=1
+y2=1
由y=-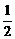 及求得的椭圆方程可得,椭圆上的点(-
及求得的椭圆方程可得,椭圆上的点(-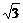 ,-
,-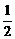 ),点(
),点(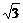 ,-
,-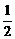 )到点P的距离都是
)到点P的距离都是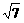

解法二:根据题设条件,设椭圆的参数方程是
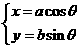 其中a>b>0待定,0≤θ<2π,
其中a>b>0待定,0≤θ<2π,
∵e=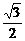 ,∴a=2b
,∴a=2b
设椭圆上的点(x,y)到点P的距离为d,则
d2=x2+(y-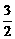 )2=a2cos2θ+(bsinθ-
)2=a2cos2θ+(bsinθ-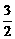 )2=-3b2·(sinθ+
)2=-3b2·(sinθ+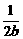 )2+4b2+3
)2+4b2+3
如果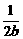 >1,即b<
>1,即b<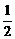 ,
,
则当sinθ=-1时,d2(从而d)有最大值,
由题设得(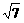 )2=(b+
)2=(b+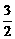 ) 2,
) 2,
由此得b=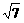 -
-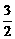 >
>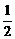 ,与b<
,与b<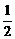 矛盾
矛盾
因此必有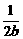 ≤1成立,于是当sinθ=-
≤1成立,于是当sinθ=-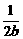 时,d2(从而d)有最大值,
时,d2(从而d)有最大值,
由题设得(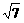 )2=4b2+3
)2=4b2+3 由此得b=1,a=2
由此得b=1,a=2
所以椭圆参数方程为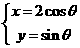
消去参数得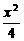 +y2=1,
+y2=1,
由sinθ=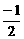 ,cosθ=±
,cosθ=±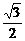 知椭圆上的点(-
知椭圆上的点(-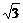 ,-
,-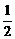 ),(
),(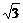 ,-
,-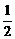 )到P点的距离都是
)到P点的距离都是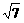

6、3-k2>1-k>0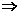 k∈(-1,1),方程所表示的曲线是焦点在x轴上的椭圆; 1-k>3-k2>0
k∈(-1,1),方程所表示的曲线是焦点在x轴上的椭圆; 1-k>3-k2>0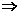 k∈(-
k∈(-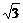 ,-1),方程所表示的曲线是焦点在y轴上的椭圆;1-k=3-k2>0
,-1),方程所表示的曲线是焦点在y轴上的椭圆;1-k=3-k2>0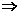 k=-1,表示的是一个圆;(1-k)(3-k2)<0
k=-1,表示的是一个圆;(1-k)(3-k2)<0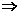 k∈(-∞,-
k∈(-∞,-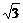 )∪(1,
)∪(1,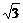 ),表示的是双曲线;k=1,k=-
),表示的是双曲线;k=1,k=-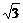 ,表示的是两条平行直线;k=
,表示的是两条平行直线;k=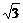 ,表示的图形不存在
,表示的图形不存在
10.(2006山东卷)双曲线C与椭圆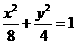 有相同的焦点,直线y=
有相同的焦点,直线y=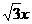 为C的一条渐近线.
为C的一条渐近线.
(1)求双曲线C的方程;
(2)过点P(0,4)的直线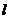 ,交双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当
,交双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当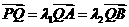 ,且
,且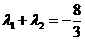 时,求Q点的坐标.
时,求Q点的坐标.
DAB 4、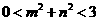
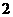 个 5、
个 5、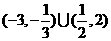
9.从椭圆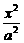 +
+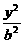 =1(a>b>0)上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴右端点A与短轴上端点B的连线AB∥OM.
=1(a>b>0)上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴右端点A与短轴上端点B的连线AB∥OM.
(1)求椭圆的离心率;
(2)若Q是椭圆上任意一点,F2是右焦点,求∠F1QF2的取值范围;
(3)过F1作AB的平行线交椭圆于C、D两点,若|CD|=3,求椭圆的方程.
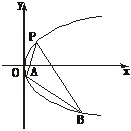
8.如下图,过抛物线y2=2px(p>0)上一定点P(x0,y0)(y0>0),作两条直线分别交抛物线于A(x1,y1)、B(x2,y2).
(1)求该抛物线上纵坐标为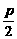 的点到其焦点F的距离;
的点到其焦点F的距离;
(2)当PA与PB的斜率存在且倾斜角互补时,求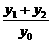 的值,并证明直线AB的斜率是非零常数.
的值,并证明直线AB的斜率是非零常数.
7.设椭圆中心是坐标原点,长轴在x轴上,离心率e=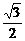 ,已知点P(0,
,已知点P(0,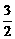 )到这个椭圆上的点的最远距离是
)到这个椭圆上的点的最远距离是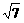 ,求这个椭圆方程,并求椭圆上到点P的距离等于
,求这个椭圆方程,并求椭圆上到点P的距离等于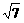 的点的坐标
的点的坐标
5.试给出方程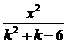 +
+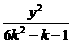 =1表示双曲线的充要条件:__________________.
=1表示双曲线的充要条件:__________________.
6 试讨论方程(1-k)x2+(3-k2)y2=4(k∈R)所表示的曲线.
试讨论方程(1-k)x2+(3-k2)y2=4(k∈R)所表示的曲线.
6.设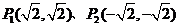 ,
,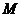 是双曲线
是双曲线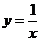 上位于第一象限的点,对于命题①
上位于第一象限的点,对于命题①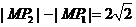 ;②以线段
;②以线段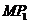 为直径的圆与圆
为直径的圆与圆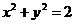 相切;③存在常数
相切;③存在常数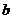 ,使得
,使得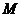 到直线
到直线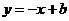 的距离等于
的距离等于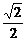
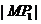 .其中所有正确命题的序号是________.
.其中所有正确命题的序号是________.
[典型例题选讲]
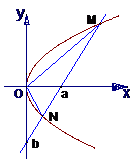 例1.如图,O为坐标原点,直线l在x轴和y轴上的截距分别是a和b(a>0,b≠0),且交抛物线y2=2px(p>0)于M(x1,y1),N(x2,y2)两点
例1.如图,O为坐标原点,直线l在x轴和y轴上的截距分别是a和b(a>0,b≠0),且交抛物线y2=2px(p>0)于M(x1,y1),N(x2,y2)两点
(1)写出直线l的截距式方程;
(2)证明: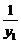 +
+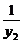 =
=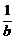 ;(3)当a=2p时,求∠MON的大小
;(3)当a=2p时,求∠MON的大小
例2.已知椭圆C的方程为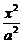 +
+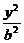 =1(a>b>0),双曲线
=1(a>b>0),双曲线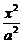 -
-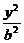 =1的两条渐近线为l1、l2 ,过椭圆C的右焦点F作直线l,使l⊥l1,又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B .(如图)
=1的两条渐近线为l1、l2 ,过椭圆C的右焦点F作直线l,使l⊥l1,又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B .(如图)
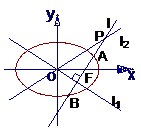 (1)当l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程;
(1)当l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程;
(2)当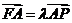 时,求
时,求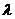 的最大值
的最大值

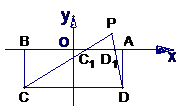
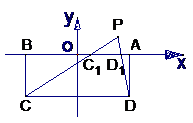
例3.如图, 矩形ABCD中, 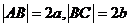 , 以AB边所在的直线为x轴, AB的中点为原点建立直角坐标系, P是x轴上方一点, 使PC、PD与线段AB分别交于
, 以AB边所在的直线为x轴, AB的中点为原点建立直角坐标系, P是x轴上方一点, 使PC、PD与线段AB分别交于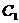 、
、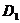 两点, 且
两点, 且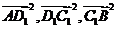 成等比数列, 求动点P的轨迹方程
成等比数列, 求动点P的轨迹方程
例4.抛物线y2=4px(p>0)的准线交x轴于M点,过点M作直线l交抛物线于A、B两点.
(1)若线段AB的垂直平分线交x轴于N(x0,0),求证:x0>3p;
(2)若直线l的斜率依次为p,p2,p3,…,线段AB的垂直平分线与x轴的交点依次为N1,N2,N3,…,当0<p<1时,求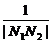 +
+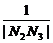 +…+
+…+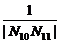 的值.
的值.
BCCDA 6、①②③
例1:(1)解:直线l的截距式方程为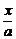 +
+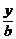 =1
=1
(2)证明:由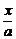 +
+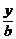 =1及y2=2px消去x可得by2+2pay-2pab=0
=1及y2=2px消去x可得by2+2pay-2pab=0
点M、N的纵坐标为y1、y2,
故y1+y2=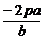 ,y1y2=-2pa
,y1y2=-2pa
所以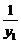 +
+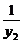 =
=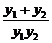 =
=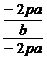 =
=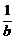

(3)解:设直线OM、ON的斜率分别为k1、k2,
则k1=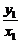 ,k2=
,k2=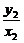

当a=2p时,由(2)知,y1y2=-2pa=-4p2,
由y12=2px1,y22=2px2,相乘得(y1y2)2=4p2x1x2,
x1x2=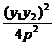 =
=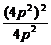 =4p2,
=4p2,
因此k1k2=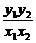 =
=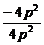 =-1
=-1
所以OM⊥ON,即∠MON=90°
例2:解:(1)∵双曲线的渐近线为y=±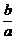 x,两渐近线夹角为60°,
x,两渐近线夹角为60°,
又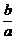 <1,∴∠POx=30°,即
<1,∴∠POx=30°,即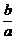 =tan30°=
=tan30°=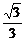
 ∴a=
∴a=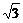 b
b
又a2+b2=4,
∴a2=3,b2=1
故椭圆C的方程为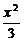 +y2=1
+y2=1
(2)由已知l:y=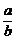 (x-c),与y=
(x-c),与y=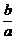 x解得P(
x解得P(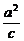 ,
,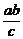 ),
),
由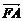 =λ
=λ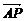 得A(
得A(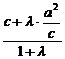 ,
,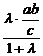 )
)
将A点坐标代入椭圆方程得
(c2+λa2)2+λ2a4=(1+λ)2a2c2
∴(e2+λ)2+λ2=e2(1+λ)2
∴λ2=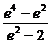 =-[(2-e2)+
=-[(2-e2)+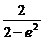 ]+3≤3-2
]+3≤3-2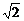

∴λ的最大值为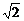 -1
-1
例3:解:
显然有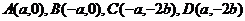 ,
,
设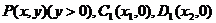 ,
,
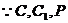 三点共线,
三点共线, 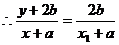 ,
,
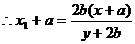 , 又
, 又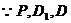 三点共线,
三点共线,
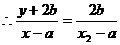 ,
, 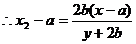 ,
, 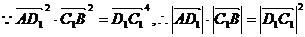 ,
,
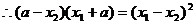 ,
, 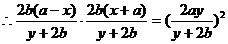 ,
,
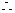 化简得动点P的轨迹方程为
化简得动点P的轨迹方程为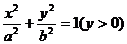

例4:(1)证明:设直线l方程为y=k(x+p),代入y2=4px.
得k2x2+(2k2p-4p)x+k2p2=0.
Δ=4(k2p-2p)2-4k2·k2p2>0,
得0<k2<1.
令A(x1,y1)、B(x2,y2),则x1+x2=-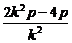 ,y1+y2=k(x1+x2+2p)=
,y1+y2=k(x1+x2+2p)=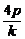 ,
,
AB中点坐标为(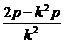 ,
,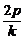 ).
).
AB垂直平分线为y-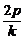 =-
=-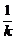 (x-
(x-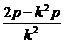 ).
).
令y=0,得x0=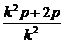 =p+
=p+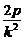 .
.
由上可知0<k2<1,∴x0>p+2p=3p.
∴x0>3p.
(2)解:∵l的斜率依次为p,p2,p3,…时,AB中垂线与x轴交点依次为N1,N2,N3,…(0<p<1).
∴点Nn的坐标为(p+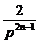 ,0).
,0).
|NnNn+1|=|(p+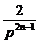 )-(p+
)-(p+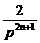 )|=
)|=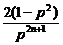 ,
,
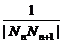 =
=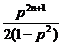 ,
,
所求的值为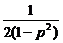 [p3+p4+…+p21]=
[p3+p4+…+p21]=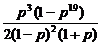 .
.
5.已知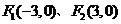 是椭圆
是椭圆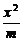 +
+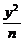 =1的两个焦点,
=1的两个焦点,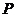 是椭圆上的点,当
是椭圆上的点,当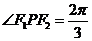 时,
时,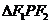 的面积最大,则有
( )
的面积最大,则有
( )
A.m=12,n=3 B.m=24,n=6 C.m=6,n=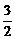 D.m=12,n=6
D.m=12,n=6
4.以正方形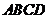 的相对顶点
的相对顶点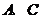 为焦点的椭圆,恰好过正方形四边的中点,则该椭圆的离心率为
( )
为焦点的椭圆,恰好过正方形四边的中点,则该椭圆的离心率为
( )
A.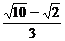 B.
B.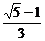 C.
C.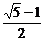 D.
D.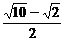
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com