
题目列表(包括答案和解析)
8.
抛物线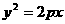 过点
过点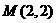 ,则点
,则点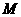 到抛物线准线的距离为_______.
到抛物线准线的距离为_______.
7.
若焦点在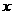 轴上的椭圆
轴上的椭圆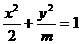 的离心率为
的离心率为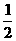 ,则
,则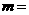 _________.
_________.
6.
椭圆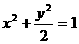 的离心率为______,其焦点到相应准线的距离为______.
的离心率为______,其焦点到相应准线的距离为______.
5.
与直线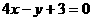 平行的抛物线
平行的抛物线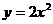 的切线方程是( )
的切线方程是( )
A.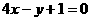 B.
B.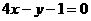
C.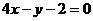 D.
D.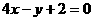
4.
已知双曲线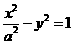
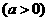 的一条渐近线与直线
的一条渐近线与直线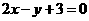 垂直,则该双曲线的准线方程是( )
垂直,则该双曲线的准线方程是( )
A.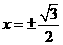 B.
B.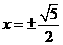 C.
C.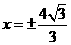 D.
D.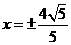
3.
若双曲线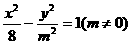 的一条准线与抛物线
的一条准线与抛物线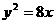 的准线重合,则双曲线的离心率为( )
的准线重合,则双曲线的离心率为( )
A.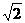 B.2
B.2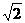 C.4 D.
C.4 D.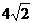
2.
椭圆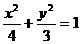 的右焦点到直线
的右焦点到直线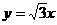 的距离是(
)
的距离是(
)
A.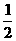 B.
B.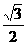 C.1 D.
C.1 D.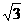
1.
双曲线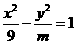 的焦距是10,则实数
的焦距是10,则实数 的值是(
)
的值是(
)
A.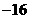 B.4 C.16 D.81
B.4 C.16 D.81
8、解:(1)由题意,设曲线方程为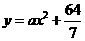 , 将点D(8,0)的坐标代入,得
, 将点D(8,0)的坐标代入,得 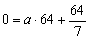 .
. 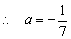 . ∴ 曲线方程为
. ∴ 曲线方程为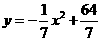 .
.
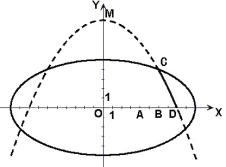 (2)设变轨点为C(x,y),根据题意可知
(2)设变轨点为C(x,y),根据题意可知
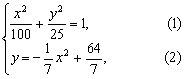
得4y2-7y-36=0,
解出y=4或y=-9/4(不合题意,舍去),
从而y=4,于是x=6或x=-6(不合题意,舍去),所以 C 点的坐标为(6,4).
应用两点之间距离公式计算,得 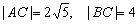 .
.
答:当观测点A、B测得AC、BC距离分别为 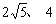 时,应向航天器发出变轨指令.
时,应向航天器发出变轨指令.
7、解:(1)在给定的直角坐标系下,设最高点为A,入水点为B,抛物线的解析式为
y=ax2+bx+c
由题意知,O、B两点的坐标依次为(0,0)、(2,-10),且顶点A的纵坐标为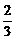 ,所以有c=0,
,所以有c=0,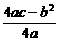 =
=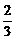 ,4a+2b+c=-10
,4a+2b+c=-10
解之得a=-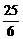 , b=
, b=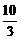 ,c=0或a=-
,c=0或a=-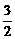 ,b=-2,c=0
,b=-2,c=0
∵抛物线对称轴在y轴右侧,∴-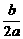 >0
>0
又∵抛物线开口向下,∴a<0
∴b>0,后一组解舍去
∴a=-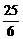 ,b=
,b=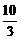 ,c=0
,c=0
∴抛物线的解析式为y=-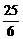 x2+
x2+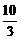 x
x
(2)当运动员在空中距池边的水平距离为3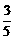 m时,即x=3
m时,即x=3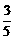 -2=
-2=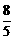 时,
时,
y=(-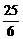 )×(
)×(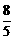 )2+
)2+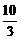 ×
×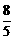 =-
=-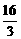 ,
,
∴此时运动员距水面的高为
10-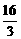 =
=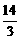 <5
<5
因此,此次跳水会出现失误
(3)当运动员在x轴上方,即y>0的区域内完成动作并做好入水姿势时,当然不会失误,但很难做到
∴当y<0时,要使跳水不出现失误,
则应有|y|≤10-5,即-y≤5
∴有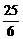 x2-
x2-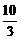 x≤5,
x≤5,
解得2-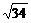 ≤x≤2+
≤x≤2+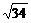

∴运动员此时距池边的距离至多为2+2+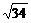 =4+
=4+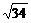 m
m
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com