
题目列表(包括答案和解析)
8、解 (1)设P点的坐标为(x1,y1),则Q点坐标为(x1,-y1),又有A1(-m,0),A2(m,0),则A1P的方程为
(1)设P点的坐标为(x1,y1),则Q点坐标为(x1,-y1),又有A1(-m,0),A2(m,0),则A1P的方程为 y=
y=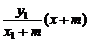 ①
①
A2Q的方程为 y=-
y=-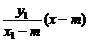 ②
②
①×②得 y2=-
y2=-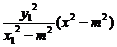 ③
③
又因点P在双曲线上,故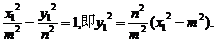
代入③并整理得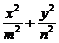 =1
=1 此即为M的轨迹方程
此即为M的轨迹方程
(2)当m≠n时,M的轨迹方程是椭圆
(ⅰ)当m>n时,焦点坐标为(±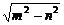 ,0),准线方程为x=±
,0),准线方程为x=±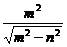 ,离心率e=
,离心率e=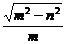 ;
;
(ⅱ)当m<n时,焦点坐标为(0,±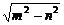 ),准线方程为y=±
),准线方程为y=±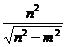 ,离心率e=
,离心率e=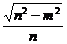

7、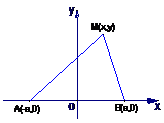 解
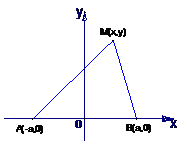
解 建立坐标系如图所示,
建立坐标系如图所示,
设|AB|=2a,则A(-a,0),B(a,0)
设M(x,y)是轨迹上任意一点
则由题设,得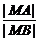 =λ,坐标代入,得
=λ,坐标代入,得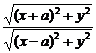 =λ,化简得
=λ,化简得
(1-λ2)x2+(1-λ2)y2+2a(1+λ2)x+(1-λ2)a2=0
(1)当λ=1时,即|MA|=|MB|时,点M的轨迹方程是x=0,点M的轨迹是直线(y轴)
(2)当λ≠1时,点M的轨迹方程是x2+y2+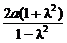 x+a2=0
x+a2=0 点M的轨迹是以(-
点M的轨迹是以(-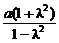 ,0)为圆心,
,0)为圆心,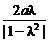 为半径的圆
为半径的圆
6、解 由e=
由e=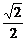 ,可设椭圆方程为
,可设椭圆方程为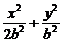 =1,
=1,
又设A(x1,y1)、B(x2,y2),则x1+x2=4,y1+y2=2,
又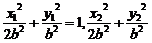 =1,两式相减,得
=1,两式相减,得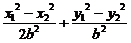 =0,
=0,
即(x1+x2)(x1-x2)+2(y1+y2)(y1-y2)=0
化简得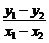 =-1,故直线AB的方程为y=-x+3,
=-1,故直线AB的方程为y=-x+3,
代入椭圆方程得3x2-12x+18-2b2=0 有Δ=24b2-72>0,
有Δ=24b2-72>0,
 又|AB|=
又|AB|=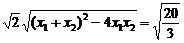 ,
,
得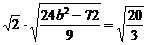 ,解得b2=8
,解得b2=8
故所求椭圆方程为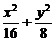 =1
=1
5、解 |MF|max=a+c,|MF|min=a-c,则(a+c)(a-c)=a2-c2=b2,
|MF|max=a+c,|MF|min=a-c,则(a+c)(a-c)=a2-c2=b2,
∴b2=4,设椭圆方程为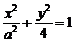 ①
①
设过M1和M2的直线方程为y=-x+m ②
将②代入①得 (4+a2)x2-2a2mx+a2m2-4a2=0 ③
(4+a2)x2-2a2mx+a2m2-4a2=0 ③
设M1(x1,y1)、M2(x2,y2),M1M2的中点为(x0,y0),
则x0=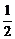 (x1+x2)=
(x1+x2)=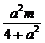 ,y0=-x0+m=
,y0=-x0+m=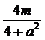

代入y=x,得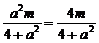 ,
,
由于a2>4,∴m=0,∴由③知x1+x2=0,x1x2=-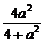 ,
,
又|M1M2|=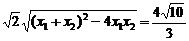 ,
,
代入x1+x2,x1x2可解a2=5,故所求椭圆方程为
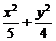 =1
=1
7. 已知A、B为两定点,动点M到A与到B的距离比为常数λ,求点M的轨迹方程,并注明轨迹是什么曲线
已知A、B为两定点,动点M到A与到B的距离比为常数λ,求点M的轨迹方程,并注明轨迹是什么曲线
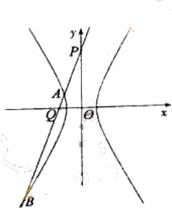
8 已知双曲线
已知双曲线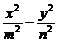 =1(m>0,n>0)的顶点为A1、A2,与y轴平行的直线l交双曲线于点P、Q .
=1(m>0,n>0)的顶点为A1、A2,与y轴平行的直线l交双曲线于点P、Q .
(1)求直线A1P与A2Q交点M的轨迹方程;
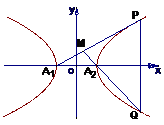 (2)当m≠n时,求所得圆锥曲线的焦点坐标、准线方程和离心率
(2)当m≠n时,求所得圆锥曲线的焦点坐标、准线方程和离心率
9 已知椭圆
已知椭圆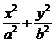 =1(a>b>0) ,点P为其上一点,F1、F2为椭圆的焦点,∠F1PF2的外角平分线为l,点F2关于l的对称点为Q,F2Q交l于点R .
=1(a>b>0) ,点P为其上一点,F1、F2为椭圆的焦点,∠F1PF2的外角平分线为l,点F2关于l的对称点为Q,F2Q交l于点R .
(1)当P点在椭圆上运动时,求R形成的轨迹方程;
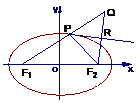 (2)设点R形成的曲线为C,直线l:y=k(x+
(2)设点R形成的曲线为C,直线l:y=k(x+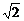 a)与曲线C相交于A、B两点,当△AOB的面积取得最大值时,求k的值
a)与曲线C相交于A、B两点,当△AOB的面积取得最大值时,求k的值
1(抛物线方程改为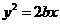 )D 2、D
3、
)D 2、D
3、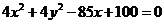 4、
4、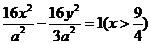
2.已知双曲线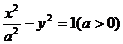 的一条准线与抛物线
的一条准线与抛物线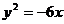 的准线重合,则该双曲线的离心率为
( )
的准线重合,则该双曲线的离心率为
( )
A.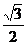 B.
B.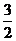 C.
C.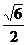 D.
D.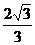
3 高为5 m和3 m的两根旗杆竖在水平地面上,且相距10 m,如果把两旗杆底部的坐标分别确定为A(-5,0)、B(5,0),则地面观测两旗杆顶端仰角相等的点的轨迹方程是________
高为5 m和3 m的两根旗杆竖在水平地面上,且相距10 m,如果把两旗杆底部的坐标分别确定为A(-5,0)、B(5,0),则地面观测两旗杆顶端仰角相等的点的轨迹方程是________
4 △ABC中,A为动点,B、C为定点,B(-
△ABC中,A为动点,B、C为定点,B(-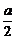 ,0),C(
,0),C(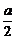 ,0),且满足条件sinC-sinB=
,0),且满足条件sinC-sinB=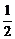 sinA,则动点A的轨迹方程为_________
sinA,则动点A的轨迹方程为_________
5 已知椭圆的中心在坐标原点,焦点在x轴上,它的一个焦点为F,M是椭圆上的任意点,|MF|的最大值和最小值的几何平均数为2,椭圆上存在着以y=x为轴的对称点M1和M2,且|M1M2|=
已知椭圆的中心在坐标原点,焦点在x轴上,它的一个焦点为F,M是椭圆上的任意点,|MF|的最大值和最小值的几何平均数为2,椭圆上存在着以y=x为轴的对称点M1和M2,且|M1M2|=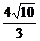 ,试求椭圆的方程
,试求椭圆的方程
6 已知圆C1的方程为(x-2)2+(y-1)2=
已知圆C1的方程为(x-2)2+(y-1)2=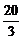 ,椭圆C2的方程为
,椭圆C2的方程为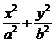 =1(a>b>0),C2的离心率为
=1(a>b>0),C2的离心率为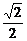 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程
1.若椭圆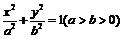 的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2px的焦点分成5:3两段,则此椭圆的离心率为
( )
的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2px的焦点分成5:3两段,则此椭圆的离心率为
( )
A.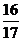 B.
B.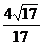 C.
C.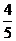 D.
D.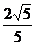
10、解:(Ⅰ)设双曲线方程为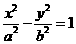 由椭圆
由椭圆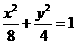 求得两焦点为
求得两焦点为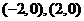 ,
,
 对于双曲线
对于双曲线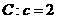 ,又
,又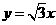 为双曲线
为双曲线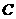 的一条渐近线
的一条渐近线

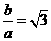 解得
解得 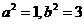 ,
,
 双曲线
双曲线 的方程为
的方程为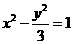
(Ⅱ)解法一:
由题意知直线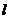 的斜率
的斜率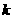 存在且不等于零。
存在且不等于零。
设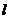 的方程:
的方程: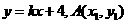 ,
,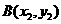 则
则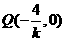
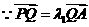
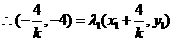
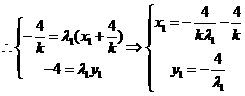

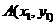 在双曲线
在双曲线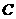 上,
上,
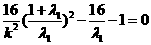

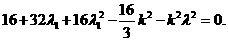

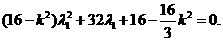
同理有: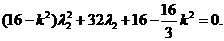
若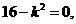 则直线
则直线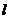 过顶点,不合题意.
过顶点,不合题意.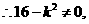
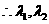 是二次方程
是二次方程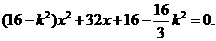 的两根.
的两根.
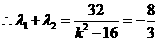
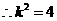 ,
,
此时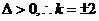 .
. 所求
所求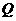 的坐标为
的坐标为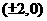 .
.
解法二:由题意知直线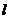 的斜率
的斜率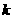 存在且不等于零
存在且不等于零
设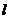 的方程,
的方程,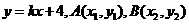 ,则
,则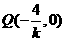 .
.
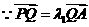 ,
,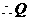 分
分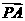 的比为
的比为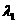 .
.
由定比分点坐标公式得
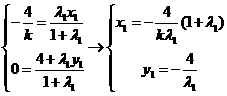
下同解法一
解法三:由题意知直线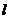 的斜率
的斜率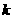 存在且不等于零
存在且不等于零
设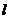 的方程:
的方程: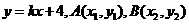 ,则
,则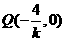 .
.
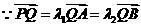 ,
,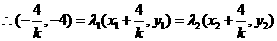 .
.
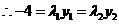 ,
,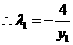 ,
,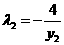 ,
,
又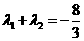 ,
,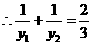 ,即
,即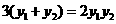
将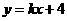 代入
代入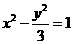 得
得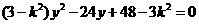
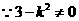 ,否则
,否则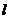 与渐近线平行。
与渐近线平行。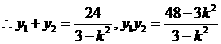 。
。
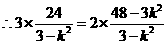
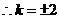
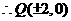
解法四:由题意知直线l得斜率k存在且不等于零,设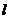 的方程:
的方程: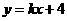 ,
,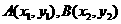 ,则
,则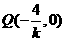
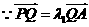 ,
,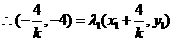 。
。
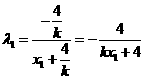
同理 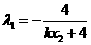
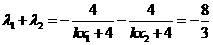 .
.
即 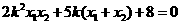 。 (*)
。 (*)
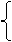 又
又 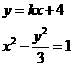
消去y得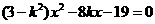 .
.
当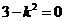 时,则直线l与双曲线得渐近线平行,不合题意,
时,则直线l与双曲线得渐近线平行,不合题意,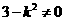 。
。
由韦达定理有:
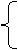
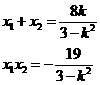
代入(*)式得 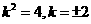
 所求Q点的坐标为
所求Q点的坐标为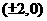 。
。
9、解:(1)由已知可设M(-c,y),
则有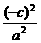 +
+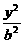 =1.
=1.
∵M在第二象限,∴M(-c,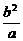 ).
).
又由AB∥OM,可知kAB=kOM.
∴-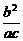 =-
=-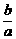 .∴b=c.∴a=
.∴b=c.∴a=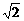 b.
b.
∴e=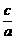 =
=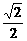 .
.
(2)设|F1Q|=m,|F2Q|=n,
则m+n=2a,mn>0.|F1F2|=2c,a2=2c2,
∴cos∠F1QF2=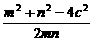
=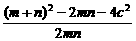 =
=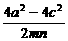 -1
-1
=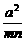 -1≥
-1≥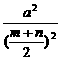 -1=
-1=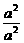 -1=0.
-1=0.
当且仅当m=n=a时,等号成立.
故∠F1QF2∈[0,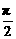 ].
].
(3)∵CD∥AB,kCD=-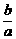 =-
=-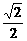 .
.
设直线CD的方程为y=-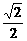 (x+c),
(x+c),
即y=-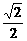 (x+b).
(x+b).
|
|
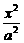 +
+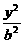 =1,
=1,
y=-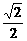 (x+b).
(x+b).
(a2+2b2)x2+2a2bx-a2b2=0.
设C(x1,y1)、D(x2,y2),∵a2=2b2,
∴x1+x2=-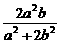 =-
=-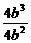 =-b,
=-b,
x1·x2=-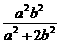 =-
=-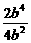 =-
=-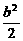 .
.
∴|CD|=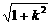 |x1-x2|
|x1-x2|
=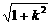 ·
·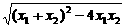
=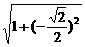 ·
·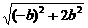 =
=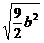 =3.
=3.
∴b2=2,则a2=4.
∴椭圆的方程为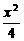 +
+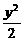 =1.
=1.
8、解:(1)当y=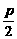 时,x=
时,x=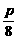 .
.
又抛物线y2=2px的准线方程为x=-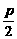 ,
,
由抛物线定义得
所求距离为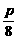 -(-
-(-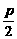 )=
)=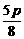 .
.
(2)设直线PA的斜率为kPA,直线PB的斜率为kPB.
由y12=2px1,y02=2px0,
相减得(y1-y0)(y1+y0)=2p(x1-x0),
故kPA=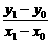 =
=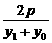 (x1≠x0).
(x1≠x0).
同理可得kPB=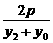 (x2≠x0).
(x2≠x0).
由PA、PB倾斜角互补知kPA=-kPB,
即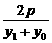 =-
=-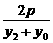 ,所以y1+y2=-2y0,
,所以y1+y2=-2y0,
故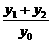 =-2.
=-2.
设直线AB的斜率为kAB.
由y22=2px2,y12=2px1,
相减得(y2-y1)(y2+y1)=2p(x2-x1),
所以kAB=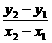 =
=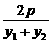 (x1≠x2).
(x1≠x2).
将y1+y2=-2y0(y0>0)代入得
kAB=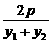 =-
=-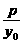 ,所以kAB是非零常数.
,所以kAB是非零常数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com