
题目列表(包括答案和解析)
15.(湖北17).(本小题满分12分)
已知函数 (m为常数,且m>0)有极大值9.
(m为常数,且m>0)有极大值9.
(Ⅰ)求m的值;
(Ⅱ)若斜率为-5的直线是曲线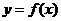 的切线,求此直线方程.
的切线,求此直线方程.
解:(Ⅰ) f’(x)=3x2+2mx-m2=(x+m)(3x-m)=0,则x=-m或x=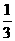 m,
m,
当x变化时,f’(x)与f(x)的变化情况如下表:
|
x |
(-∞,-m) |
-m |
(-m,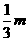 ) ) |
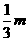 |
(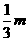 ,+∞) ,+∞) |
|
f’(x) |
 + + |
0 |
- |
0 |
+ |
|
f (x) |
|
极大值 |
|
极小值 |
|
从而可知,当x=-m时,函数f(x)取得极大值9,
即f(-m)=-m3+m3+m3+1=9,∴m=2.
(Ⅱ)由(Ⅰ)知,f(x)=x3+2x2-4x+1,
依题意知f’(x)=3x2+4x-4=-5,∴x=-1或x=-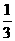 .
.
又f(-1)=6,f(-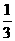 )=
)=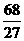 ,
,
所以切线方程为y-6=-5(x+1),或y-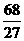 =-5(x+
=-5(x+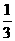 ),
),
即5x+y-1=0,或135x+27y-23=0.
14.(重庆19)(本小题满分12分,(Ⅰ)小问6分,(Ⅱ)小问6分.)
设函数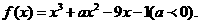 若曲线y=f(x)的斜率最小的切线与直线12x+y=6平行,求:
若曲线y=f(x)的斜率最小的切线与直线12x+y=6平行,求:
(Ⅰ)a的值;
(Ⅱ)函数f(x)的单调区间.
解:(Ⅰ)因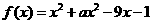
所以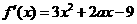
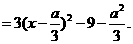
即当
因斜率最小的切线与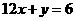 平行,即该切线的斜率为-12,
平行,即该切线的斜率为-12,
所以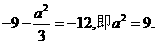
解得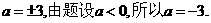
(Ⅱ)由(Ⅰ)知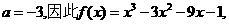

13.(浙江21)(本题15分)已知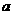 是实数,函数
是实数,函数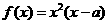 。
。
(Ⅰ)若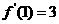 ,求
,求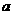 的值及曲线
的值及曲线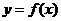 在点
在点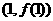 处的切线方程;
处的切线方程;
(Ⅱ)求 在区间
在区间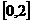 上的最大值。
上的最大值。
(Ⅰ)解: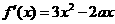 ,
,
因为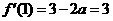 ,
,
所以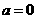 .
.
又当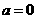 时,
时,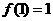 ,
,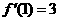 ,
,
所以曲线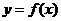 在
在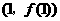 处的切线方程为
处的切线方程为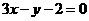 .
.
(Ⅱ)解:令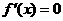 ,解得
,解得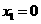 ,
,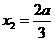 .
.
当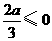 ,即
,即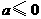 时,
时, 在
在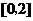 上单调递增,从而
上单调递增,从而
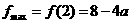 .
.
当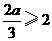 ,即
,即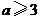 时,
时, 在
在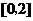 上单调递减,从而
上单调递减,从而
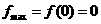 .
.
当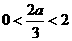 ,即
,即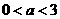 时,
时, 在
在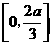 上单调递减,在
上单调递减,在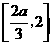 上单调递增,从而
上单调递增,从而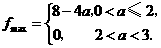
综上所述, 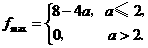
12.(天津21)(本小题满分14分)
设函数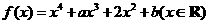 ,其中
,其中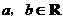 .
.
(Ⅰ)当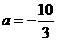 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(Ⅱ)若函数 仅在
仅在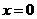 处有极值,求
处有极值,求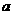 的取值范围;
的取值范围;
(Ⅲ)若对于任意的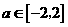 ,不等式
,不等式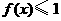 在
在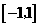 上恒成立,求
上恒成立,求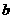 的取值范围.
的取值范围.
(Ⅰ)解: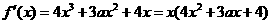 .
.
当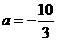 时,
时,
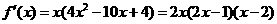 .
.
令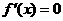 ,解得
,解得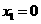 ,
,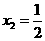 ,
,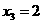 .
.
当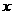 变化时,
变化时,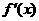 ,
, 的变化情况如下表:
的变化情况如下表:
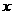 |
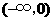 |
 |
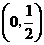 |
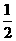 |
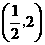 |
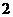 |
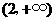 |
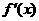 |
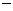 |
 |
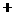 |
 |
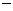 |
 |
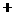 |
 |
↘ |
极小值 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以 在
在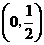 ,
,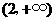 内是增函数,在
内是增函数,在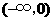 ,
,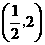 内是减函数.
内是减函数.
(Ⅱ)解: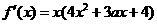 ,显然
,显然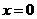 不是方程
不是方程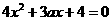 的根.
的根.
为使 仅在
仅在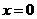 处有极值,必须
处有极值,必须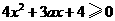 恒成立,即有
恒成立,即有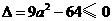 .
.
解此不等式,得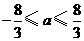 .这时,
.这时,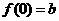 是唯一极值.
是唯一极值.
因此满足条件的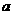 的取值范围是
的取值范围是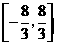 .
.
(Ⅲ)解:由条件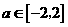 可知
可知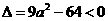 ,从而
,从而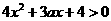 恒成立.
恒成立.
当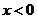 时,
时,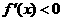 ;当
;当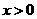 时,
时,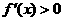 .
.
因此函数 在
在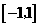 上的最大值是
上的最大值是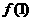 与
与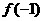 两者中的较大者.
两者中的较大者.
为使对任意的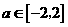 ,不等式
,不等式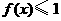 在
在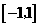 上恒成立,当且仅当
上恒成立,当且仅当
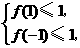 即
即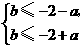
在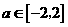 上恒成立.
上恒成立.
所以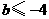 ,因此满足条件的
,因此满足条件的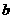 的取值范围是
的取值范围是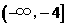 .
.
11.(四川20)(本小题满分12分)
设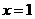 和
和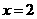 是函数
是函数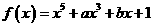 的两个极值点。
的两个极值点。
(Ⅰ)求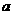 和
和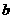 的值;
的值;
(Ⅱ)求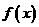 的单调区间
的单调区间
[解]:(Ⅰ)因为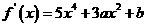
由假设知: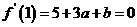
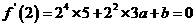
解得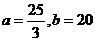
(Ⅱ)由(Ⅰ)知
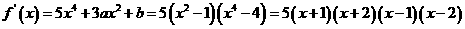
当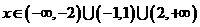 时,
时,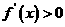
当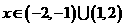 时,
时,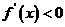
因此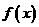 的单调增区间是
的单调增区间是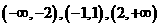
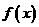 的单调减区间是
的单调减区间是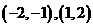
10.(山东21)(本小题满分12分)
设函数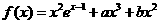 ,已知
,已知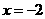 和
和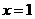 为
为 的极值点.
的极值点.
(Ⅰ)求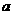 和
和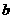 的值;
的值;
(Ⅱ)讨论 的单调性;
的单调性;
(Ⅲ)设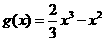 ,试比较
,试比较 与
与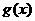 的大小.
的大小.
解:(Ⅰ)因为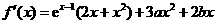
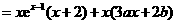 ,
,
又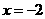 和
和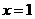 为
为 的极值点,所以
的极值点,所以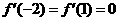 ,
,
因此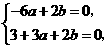
解方程组得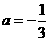 ,
,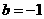 .
.
(Ⅱ)因为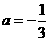 ,
,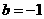 ,
,
所以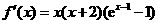 ,
,
令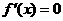 ,解得
,解得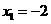 ,
,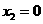 ,
,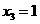 .
.
因为当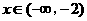
 时,
时,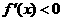 ;
;
当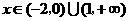 时,
时,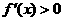 .
.
所以 在
在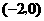 和
和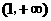 上是单调递增的;
上是单调递增的;
在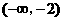 和
和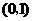 上是单调递减的.
上是单调递减的.
(Ⅲ)由(Ⅰ)可知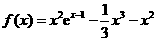 ,
,
故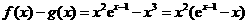 ,
,
令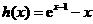 ,
,
则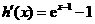 .
.
令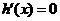 ,得
,得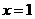 ,
,
因为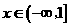 时,
时,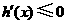 ,
,
所以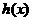 在
在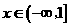 上单调递减.
上单调递减.
故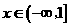 时,
时, ;
;
因为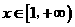 时,
时,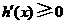 ,
,
所以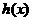 在
在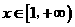 上单调递增.
上单调递增.
故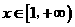 时,
时, .
.
所以对任意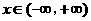 ,恒有
,恒有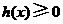 ,又
,又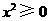 ,
,
因此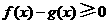 ,
,
故对任意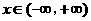 ,恒有
,恒有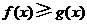 .
.
9.(全国Ⅱ21)(本小题满分12分)
设 ,函数
,函数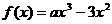 .
.
(Ⅰ)若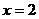 是函数
是函数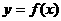 的极值点,求
的极值点,求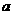 的值;
的值;
(Ⅱ)若函数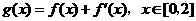 ,在
,在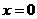 处取得最大值,求
处取得最大值,求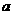 的取值范围.
的取值范围.
解:(Ⅰ)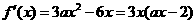 .
.
因为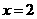 是函数
是函数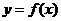 的极值点,所以
的极值点,所以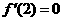 ,即
,即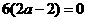 ,因此
,因此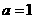 .
.
经验证,当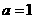 时,
时,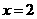 是函数
是函数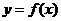 的极值点.··············································· 4分
的极值点.··············································· 4分
(Ⅱ)由题设,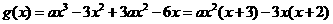 .
.
当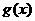 在区间
在区间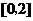 上的最大值为
上的最大值为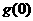 时,
时,
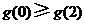 ,
,
即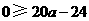 .
.
故得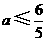 .··············································································································· 9分
.··············································································································· 9分
反之,当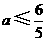 时,对任意
时,对任意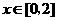 ,
,
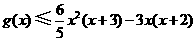
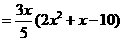
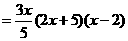
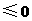 ,
,
而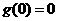 ,故
,故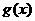 在区间
在区间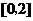 上的最大值为
上的最大值为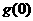 .
.
综上,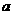 的取值范围为
的取值范围为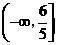 . 12分
. 12分
8.(全国Ⅰ21)(本小题满分12分)
已知函数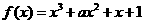 ,
, .
.
(Ⅰ)讨论函数 的单调区间;
的单调区间;
(Ⅱ)设函数 在区间
在区间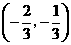 内是减函数,求
内是减函数,求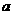 的取值范围.
的取值范围.
解:(1)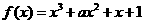
求导: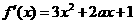
当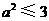 时,
时,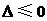 ,
,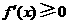
 在
在 上递增
上递增
当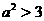 ,
,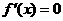 求得两根为
求得两根为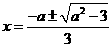
即 在
在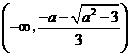 递增,
递增,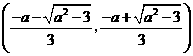 递减,
递减,
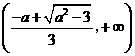 递增
递增
(2)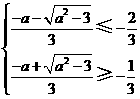 ,且
,且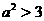
解得: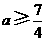
7.(辽宁22)(本小题满分14分)
设函数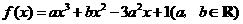 在
在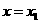 ,
,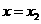 处取得极值,且
处取得极值,且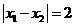 .
.
(Ⅰ)若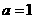 ,求
,求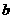 的值,并求
的值,并求 的单调区间;
的单调区间;
(Ⅱ)若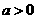 ,求
,求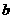 的取值范围.
的取值范围.
解: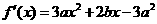 .①················································································ 2分
.①················································································ 2分
(Ⅰ)当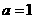 时,
时,
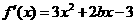 ;
;
由题意知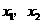 为方程
为方程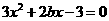 的两根,所以
的两根,所以
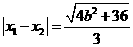 .
.
由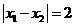 ,得
,得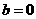 .··························································································· 4分
.··························································································· 4分
从而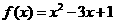 ,
,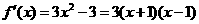 .
.
当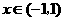 时,
时,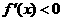 ;当
;当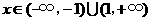 时,
时,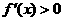 .
.
故 在
在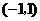 单调递减,在
单调递减,在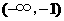 ,
,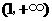 单调递增.···································· 6分
单调递增.···································· 6分
(Ⅱ)由①式及题意知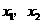 为方程
为方程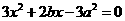 的两根,
的两根,
所以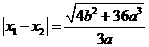 .
.
从而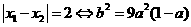 ,
,
由上式及题设知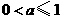 .························································································· 8分
.························································································· 8分
考虑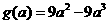 ,
,
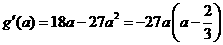 .········································································ 10分
.········································································ 10分
故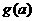 在
在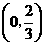 单调递增,在
单调递增,在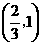 单调递减,从而
单调递减,从而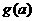 在
在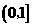 的极大值为
的极大值为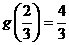 .
.
又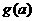 在
在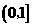 上只有一个极值,所以
上只有一个极值,所以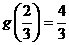 为
为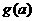 在
在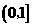 上的最大值,且最小值为
上的最大值,且最小值为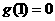 .
.
所以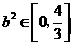 ,即
,即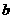 的取值范围为
的取值范围为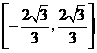 .··············································· 14分
.··············································· 14分
6.(湖南21)已知函数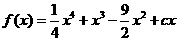 有三个极值点。
有三个极值点。
(I)证明: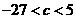 ;
;
(II)若存在实数c,使函数 在区间
在区间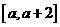 上单调递减,求
上单调递减,求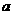 的取值范围。
的取值范围。
解:(I)因为函数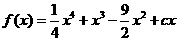 有三个极值点,
有三个极值点,
所以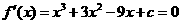 有三个互异的实根.
有三个互异的实根.
设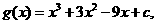 则
则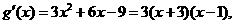
当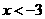 时,
时,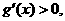
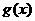 在
在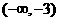 上为增函数;
上为增函数;
当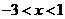 时,
时,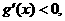
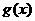 在
在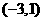 上为减函数;
上为减函数;
当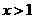 时,
时,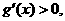
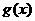 在
在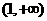 上为增函数;
上为增函数;
所以函数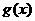 在
在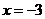 时取极大值,在
时取极大值,在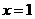 时取极小值.
时取极小值.
当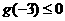 或
或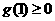 时,
时,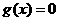 最多只有两个不同实根.
最多只有两个不同实根.
因为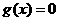 有三个不同实根, 所以
有三个不同实根, 所以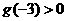 且
且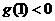 .
.
即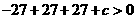 ,且
,且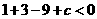 ,
,
解得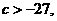 且
且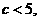 故
故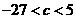 .
.
(II)由(I)的证明可知,当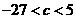 时,
时,  有三个极值点.
有三个极值点.
不妨设为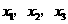 (
(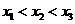 ),则
),则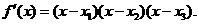
所以 的单调递减区间是
的单调递减区间是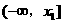 ,
,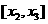
若 在区间
在区间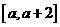 上单调递减,
上单调递减,
则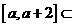
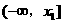 , 或
, 或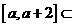
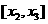 ,
,
若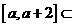
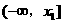 ,则
,则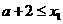 .由(I)知,
.由(I)知,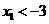 ,于是
,于是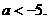
若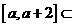
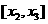 ,则
,则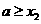 且
且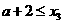 .由(I)知,
.由(I)知,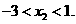
又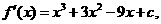 当
当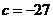 时,
时,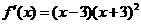 ;
;
当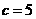 时,
时,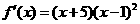 .
.
因此, 当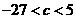 时,
时,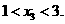 所以
所以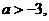 且
且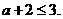
即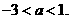 故
故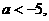 或
或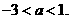 反之, 当
反之, 当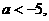 或
或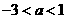 时,
时,
总可找到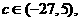 使函数
使函数 在区间
在区间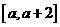 上单调递减.
上单调递减.
综上所述, 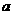 的取值范围是
的取值范围是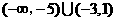 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com