
题目列表(包括答案和解析)
1.(安徽10)若过点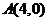 的直线
的直线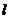 与曲线
与曲线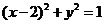 有公共点,则直线
有公共点,则直线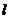 的斜率的取值范围为( D )
的斜率的取值范围为( D )
A.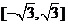 B.
B.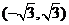 C.
C.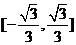 D.
D.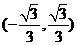
20.(陕西19)(本小题满分12分)
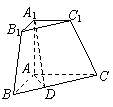
三棱锥被平行于底面 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为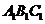 ,
,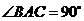 ,
,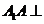 平面
平面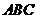 ,
,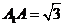 ,
,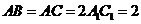 ,
,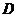 为
为 中点.
中点.
 (Ⅰ)证明:平面
(Ⅰ)证明:平面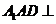 平面
平面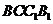 ;
;
(Ⅱ)求二面角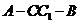 的大小.
的大小.
解法一:(Ⅰ)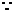
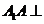 平面
平面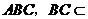 平面
平面 ,
,
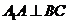 .在
.在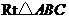 中,
中,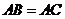 ,
,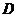 为
为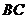 中点
中点
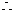
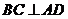 .又
.又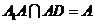 ,
,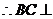 平面
平面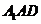 ,
,
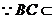 平面
平面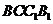 ,
,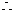 平面
平面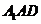
 平面
平面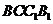 .
.
(Ⅱ)如图,作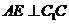 交
交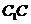 于
于 点,连接
点,连接 ,
,
 由已知得
由已知得 平面
平面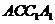 .
.
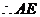 是
是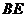 在面
在面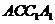 内的射影.
内的射影.
由三垂线定理知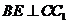 ,
,
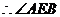 为二面角
为二面角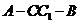 的平面角.
的平面角.
过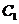 作
作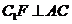 交
交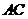 于
于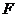 点,
点,
则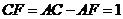 ,
,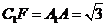 ,
,
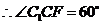 .
.
在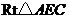 中,
中,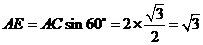 .
.
在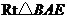 中,
中,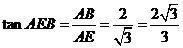 .
.
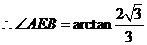 ,
,
即二面角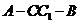 为
为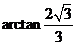 .
.
解法二:(Ⅰ)如图,建立空间直角坐标系,
则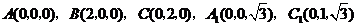 ,
,
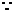
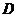 为
为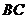 中点,
中点,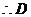 点坐标为
点坐标为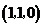 .
.
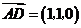 ,
, .
.
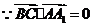 ,
,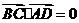 ,
,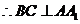 ,
,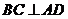 ,又
,又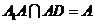 ,
,
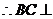 平面
平面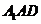 ,又
,又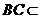 平面
平面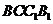 ,
,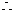 平面
平面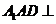 平面
平面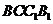 .
.
(Ⅱ)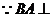 平面
平面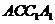 ,如图可取
,如图可取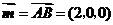 为平面
为平面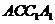 的法向量,
的法向量,
设平面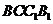 的法向量为
的法向量为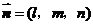 ,则
,则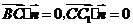 .
.
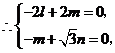
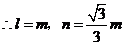 ,
,
如图,令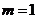 ,则
,则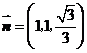 ,
,
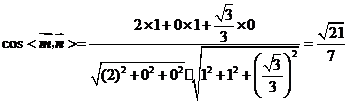 ,
,
即二面角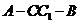 为
为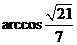 为所求.
为所求.
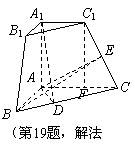
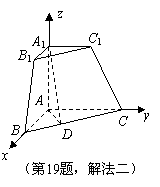
19.(湖北18).(本小题满分12分)
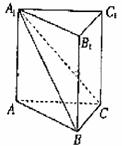 如图,在直三棱柱
如图,在直三棱柱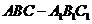 中,平面
中,平面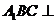 侧面
侧面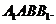
(Ⅰ)求证: 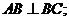
(Ⅱ)若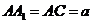 ,直线AC与平面
,直线AC与平面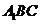 所成的角为
所成的角为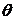 ,二面角
,二面角
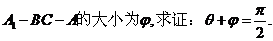

(Ⅰ)证明:如右图,过点A在平面A1ABB1内作AD⊥A1B于D,则
由平面A1BC⊥侧面A1ABB1,且平面A1BC∩侧面A1ABB1=A1B,
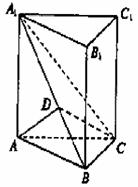 得AD⊥平面
得AD⊥平面
A1BC.又BC 平面A1BC
平面A1BC
所以AD⊥BC.
因为三棱柱ABC-A1B1C1是直三棱柱,
则AA1⊥底面ABC,所以AA1⊥BC.
又AA1∩AD=A,从而BC⊥侧面A1ABB1,
又AB 侧面A1ABB1,
侧面A1ABB1,
故AB⊥BC.
(Ⅱ)证法1:连接CD,则由(Ⅰ)知∠ACD就是直线AC与平面A1BC所成的角,∠ABA1就是二面角A1-BC-A的颊角,即∠ACD=θ,∠ABA1=j.
于是在RtΔADC中,sinθ=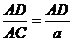 ,在RtΔADA1中,sin∠AA1D=
,在RtΔADA1中,sin∠AA1D=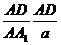 ,
,
∴sinθ=sin∠AA1D,由于θ与∠AA1D都是锐角,所以θ=∠AA1D.
又由RtΔA1AB知,∠AA1D+j=∠AA1B+j=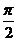 ,故θ+j=
,故θ+j=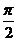 .
.
证法2:由(Ⅰ)知,以点B为坐标原点,以BC、BA、BB1所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
设AB=c(c<a=,则B(0,0,0),A(0,c,0),C(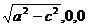 ),
),
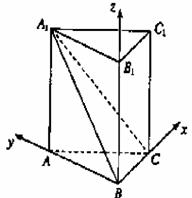 A1(0,c,a),于是
A1(0,c,a),于是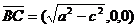 ,
,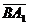 =(0,c,a),
=(0,c,a),
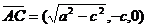 ,
,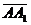 =(0,c,a)
=(0,c,a)
设平面A1BC的一个法向量为n=(x,y,z),
则由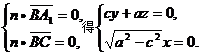
可取n=(0,-a,c),于是
n·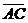 =ac>0,
=ac>0,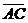 与n的夹角b为锐角,则b与q互为余角.
与n的夹角b为锐角,则b与q互为余角.
sinq=cosb=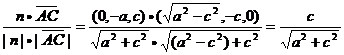 ,
,
cosj=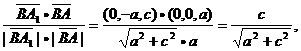
所以sinq=cosj=sin(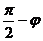 ),又0<q,j<
),又0<q,j<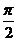 ,所以q+j=
,所以q+j=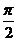 .
.
18.(重庆20)(本小题满分12分,(Ⅰ)小问6分,(Ⅱ)小问6分.)
如图(20)图,
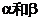 为平面,
为平面,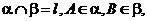 AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角
AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角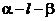 的大小为
的大小为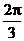 ,求:
,求:
(Ⅰ)点B到平面 的距离;
的距离;
(Ⅱ)异面直线l与AB所成的角(用反三角函数表示).
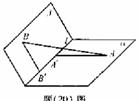
解:(1)如答(20)图,过点B′C∥A′A且使B′C=A′A.过点B作BD⊥CB′,交CB′的延长线于D.
由已知AA′⊥l,可得DB′⊥l,又已知BB′⊥l,故l⊥平面BB′D,得BD⊥l又因BD⊥CB′,从而BD⊥平面α,BD之长即为点B到平面α的距离.
因B′C⊥l且BB′⊥l,故∠BB′C为二面角α-l-β的平面角.由题意,∠BB′C=
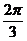 .因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=
.因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=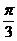 ,BD=BB′·sinBB′D
,BD=BB′·sinBB′D
=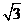 .
.
(Ⅱ)连接AC、BC.因B′C∥A′A,B′C=A′A,AA′⊥l,知A′ACB′为矩形,故AC∥l.所以∠BAC或其补角为异面直线l与AB所成的角.
在△BB′C中,B′B=2,B′C=3,∠BB′C=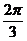 ,则由余弦定理,
,则由余弦定理,
BC=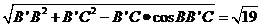 .
.
因BD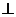 平面
平面
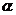 ,且DC
,且DC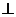 CA,由三策划线定理知AC
CA,由三策划线定理知AC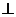 BC.
BC.
故在△ABC中,∠BCA=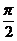 ,sinBAC=
,sinBAC=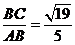 .
.
因此,异面直线l与AB所成的角为arcsin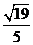 .
.
17.(浙江20)(本题14分)如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,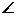 BCF=
BCF=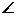 CEF=
CEF=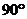 ,AD=
,AD=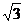 ,EF=2。
,EF=2。
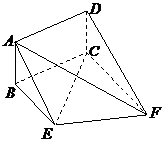 (Ⅰ)求证:AE//平面DCF;
(Ⅰ)求证:AE//平面DCF;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为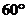 ?
?
方法一:
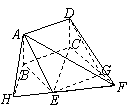 (Ⅰ)证明:过点
(Ⅰ)证明:过点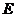 作
作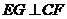 交
交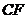 于
于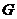 ,连结
,连结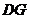 ,
,
可得四边形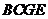 为矩形,
为矩形,
又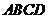 为矩形,
为矩形,
所以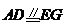 ,从而四边形
,从而四边形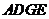 为平行四边形,
为平行四边形,
故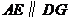 .
.
因为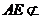 平面
平面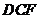 ,
,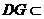 平面
平面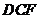 ,
,
所以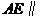 平面
平面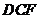 .
.
(Ⅱ)解:过点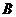 作
作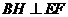 交
交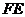 的延长线于
的延长线于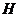 ,连结
,连结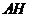 .
.
由平面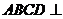 平面
平面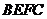 ,
,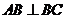 ,得
,得
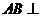 平面
平面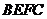 ,
,
从而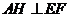 .
.
所以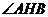 为二面角
为二面角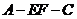 的平面角.
的平面角.
在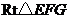 中,因为
中,因为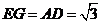 ,
,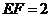 ,所以
,所以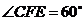 ,
,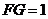 .
.
又因为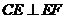 ,所以
,所以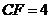 ,
,
从而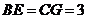 .
.
于是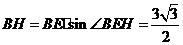 .
.
因为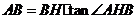 ,
,
所以当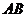 为
为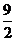 时,二面角
时,二面角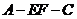 的大小为
的大小为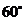 .
.
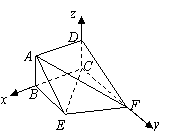 方法二:如图,以点
方法二:如图,以点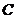 为坐标原点,以
为坐标原点,以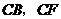 和
和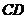 分别作为
分别作为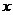 轴,
轴,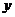 轴和
轴和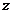 轴,建立空间直角坐标系
轴,建立空间直角坐标系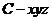 .
.
设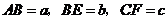 ,
,
则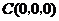 ,
,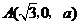 ,
,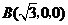 ,
,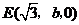 ,
,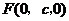 .
.
(Ⅰ)证明: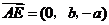 ,
,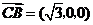 ,
,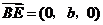 ,
,
所以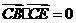 ,
,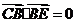 ,从而
,从而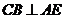 ,
,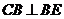 ,
,
所以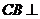 平面
平面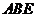 .
.
因为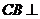 平面
平面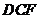 ,
,
所以平面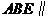 平面
平面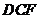 .
.
故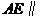 平面
平面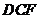 .
.
(Ⅱ)解:因为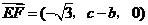 ,
,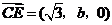 ,
,
所以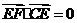 ,
,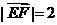 ,从而
,从而
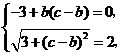
解得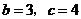 .
.
所以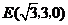 ,
,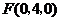 .
.
设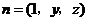 与平面
与平面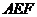 垂直,
垂直,
则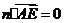 ,
,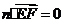 ,
,
解得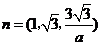 .
.
又因为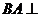 平面
平面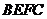 ,
,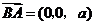 ,
,
所以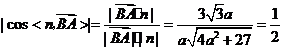 ,
,
得到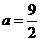 .
.
所以当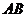 为
为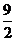 时,二面角
时,二面角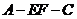 的大小为
的大小为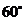 .
.
16.(天津19)(本小题满分12分)
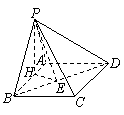
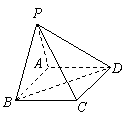 如图,在四棱锥
如图,在四棱锥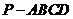 中,底面
中,底面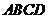 是矩形.已知
是矩形.已知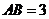 ,
,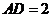 ,
,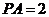 ,
,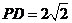 ,
,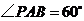 .
.
(Ⅰ)证明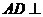 平面
平面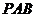 ;
;
(Ⅱ)求异面直线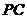 与
与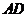 所成的角的大小;
所成的角的大小;
(Ⅲ)求二面角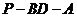 的大小.
的大小.
(Ⅰ)证明:在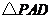 中,由题设
中,由题设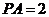 ,
,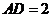 ,
,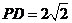 ,可得
,可得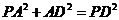 ,于是
,于是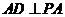 .在矩形
.在矩形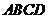 中,
中,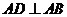 ,又
,又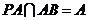 ,所以
,所以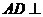 平面
平面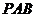 .
.
(Ⅱ)解:由题设,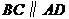 ,所以
,所以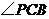 (或其补角)是异面直线
(或其补角)是异面直线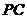 与
与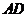 所成的角.
所成的角.
在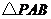 中,由余弦定理得
中,由余弦定理得
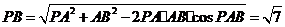 .
.
由(Ⅰ)知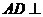 平面
平面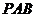 ,
,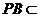 平面
平面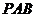 ,
,
所以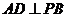 ,因而
,因而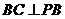 ,于是
,于是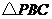 是直角三角形,
是直角三角形,
故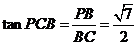 .
.
所以异面直线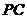 与
与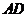 所成的角的大小为
所成的角的大小为 .
.
(Ⅲ)解:过点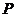 作
作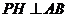 于
于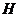 ,过点
,过点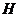 作
作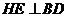 于
于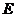 ,连结
,连结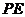 .
.
因为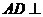 平面
平面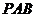 ,
,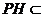 平面
平面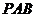 ,所以
,所以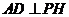 .又
.又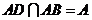 ,因而
,因而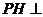 平面
平面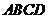 ,故
,故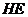 为
为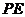 在平面
在平面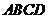 内的射影.由三垂线定理可知,
内的射影.由三垂线定理可知,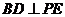 .从而
.从而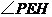 是二面角
是二面角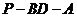 的平面角.
的平面角.
由题设可得,
 ,
,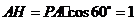 ,
,
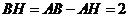 ,
,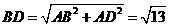 ,
,
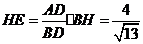 .
.
于是在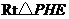 中,
中,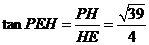 .
.
所以二面角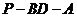 的大小为
的大小为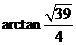 .
.
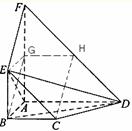
15.(四川19)(本小题满分12分)
如图,平面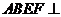 平面
平面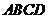 ,四边形
,四边形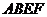 与
与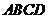 都是直角梯形,
都是直角梯形,
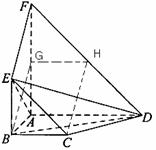
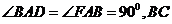
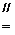
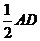 ,
,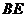
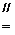
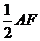 ,
,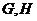 分别为
分别为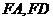 的中点
的中点
(Ⅰ)证明:四边形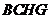 是平行四边形;
是平行四边形;
(Ⅱ)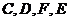 四点是否共面?为什么?
四点是否共面?为什么?
(Ⅲ)设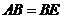 ,证明:平面
,证明:平面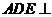 平面
平面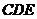 ;
;
[解1]:(Ⅰ)由题意知,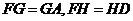
 所以
所以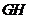
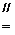
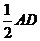
又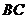
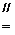
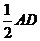 ,故
,故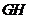
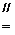
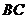
所以四边形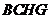 是平行四边形。
是平行四边形。
(Ⅱ)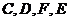 四点共面。理由如下:
四点共面。理由如下:
由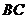
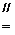
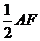 ,
,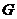 是
是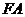 的中点知,
的中点知,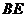
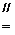
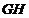 ,所以
,所以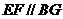
由(Ⅰ)知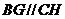 ,所以
,所以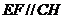 ,故
,故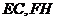 共面。又点
共面。又点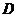 在直线
在直线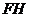 上
上
所以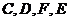 四点共面。
四点共面。
(Ⅲ)连结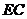 ,由
,由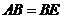 ,
,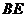
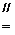
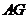 及
及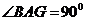 知
知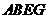 是正方形
是正方形
故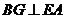 。由题设知
。由题设知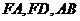 两两垂直,故
两两垂直,故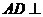 平面
平面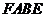 ,
,
因此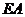 是
是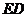 在平面
在平面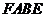 内的射影,根据三垂线定理,
内的射影,根据三垂线定理,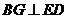
又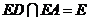 ,所以
,所以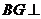 平面
平面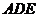
由(Ⅰ)知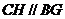 ,所以
,所以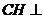 平面
平面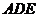 。
。
由(Ⅱ)知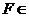 平面
平面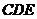 ,故
,故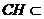 平面
平面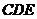 ,得平面
,得平面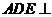 平面
平面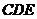
[解2]:由平面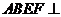 平面
平面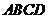 ,
,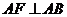 ,得
,得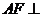 平面
平面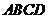 ,
,
以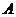 为坐标原点,射线
为坐标原点,射线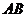 为
为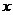 轴正半轴,建立如图所示的直角坐标系
轴正半轴,建立如图所示的直角坐标系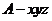
(Ⅰ)设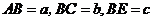 ,则由题设得
,则由题设得
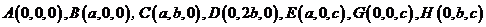
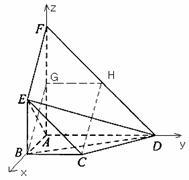 所以
所以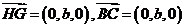
于是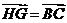
又点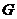 不在直线
不在直线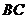 上
上
所以四边形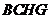 是平行四边形。
是平行四边形。
(Ⅱ)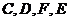 四点共面。理由如下:
四点共面。理由如下:
由题设知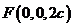 ,所以
,所以
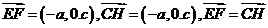 又
又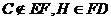 ,故
,故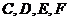 四点共面。
四点共面。
(Ⅲ)由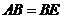 得,所以
得,所以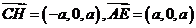
又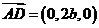 ,因此
,因此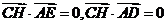
即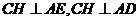
又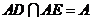 ,所以
,所以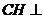 平面
平面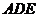
故由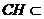 平面
平面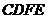 ,得平面
,得平面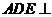 平面
平面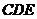
14.(上海16)(本题满分12分)
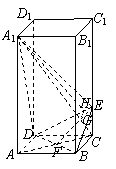
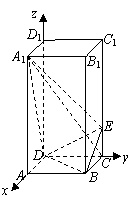
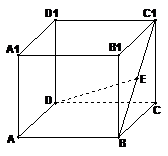 如图,在棱长为2的正方体
如图,在棱长为2的正方体 中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).
中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).
[解]过E作EF⊥BC,交BC于F,连接DF.
∵ EF⊥平面ABCD,
∴ ∠EDF是直线DE与平面ABCD所成的角. ……………4分
由题意,得EF=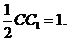
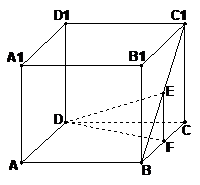 ∵
∵
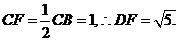 …………………………..8分
…………………………..8分
∵ EF⊥DF, ∴ 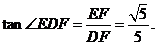 ……………..10分
……………..10分
故直线DE与平面ABCD所成角的大小是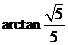 ….12分
….12分
13.(山东19)(本小题满分12分)
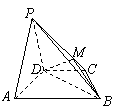 如图,在四棱锥
如图,在四棱锥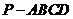 中,平面
中,平面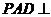 平面
平面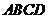 ,
,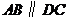 ,
,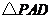 是等边三角形,已知
是等边三角形,已知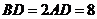 ,
,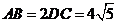 .
.
(Ⅰ)设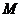 是
是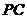 上的一点,证明:平面
上的一点,证明:平面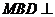 平面
平面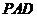 ;
;
(Ⅱ)求四棱锥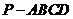 的体积.
的体积.
(Ⅰ)证明:在 中,
中,
由于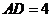 ,
,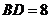 ,
,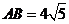 ,
,
 所以
所以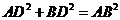 .
.
故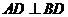 .
.
又平面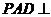 平面
平面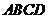 ,平面
,平面 平面
平面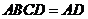 ,
,
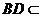 平面
平面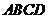 ,
,
所以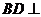 平面
平面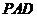 ,
,
又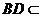 平面
平面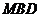 ,
,
故平面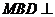 平面
平面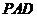 .
.
(Ⅱ)解:过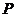 作
作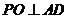 交
交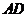 于
于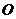 ,
,
由于平面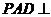 平面
平面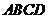 ,
,
所以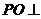 平面
平面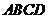 .
.
因此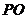 为四棱锥
为四棱锥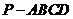 的高,
的高,
又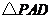 是边长为4的等边三角形.
是边长为4的等边三角形.
因此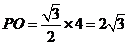 .
.
在底面四边形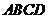 中,
中,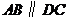 ,
,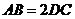 ,
,
所以四边形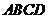 是梯形,在
是梯形,在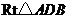 中,斜边
中,斜边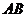 边上的高为
边上的高为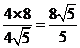 ,
,
此即为梯形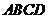 的高,
的高,
所以四边形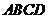 的面积为
的面积为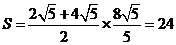 .
.
故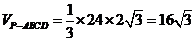 .
.
12.(全国Ⅱ20)(本小题满分12分)
如图,正四棱柱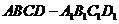 中,
中,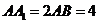 ,点
,点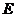 在
在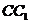 上且
上且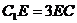 .
.
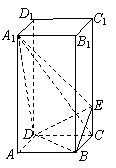 (Ⅰ)证明:
(Ⅰ)证明: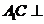 平面
平面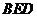 ;
;
(Ⅱ)求二面角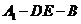 的大小.
的大小.
解法一:
依题设,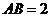 ,
,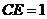 .
.
(Ⅰ)连结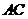 交
交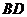 于点
于点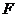 ,则
,则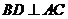 .
.
由三垂线定理知,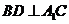 .····················································································· 3分
.····················································································· 3分
在平面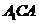 内,连结
内,连结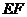 交
交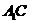 于点
于点 ,
,
 由于
由于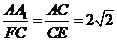 ,
,
故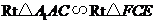 ,
,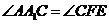 ,
,
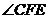 与
与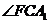 互余.
互余.
于是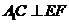 .
.
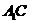 与平面
与平面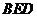 内两条相交直线
内两条相交直线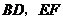 都垂直,
都垂直,
所以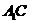
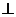 平面
平面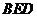 .································································································ 6分
.································································································ 6分
(Ⅱ)作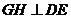 ,垂足为
,垂足为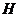 ,连结
,连结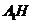 .由三垂线定理知
.由三垂线定理知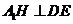 ,
,
故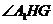 是二面角
是二面角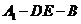 的平面角.································································· 8分
的平面角.································································· 8分
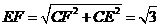 ,
,
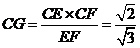 ,
,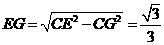 .
.
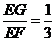 ,
,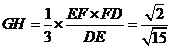 .
.
又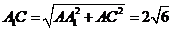 ,
,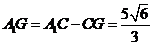 .
.
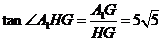 .
.
 所以二面角
所以二面角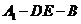 的大小为
的大小为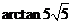 .··························································· 12分
.··························································· 12分
解法二:
以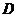 为坐标原点,射线
为坐标原点,射线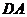 为
为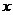 轴的正半轴,
轴的正半轴,
建立如图所示直角坐标系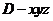 .
.
依题设,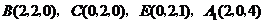 .
.
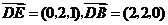 ,
,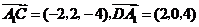 .··································· 3分
.··································· 3分
(Ⅰ)因为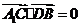 ,
,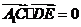 ,
,
故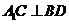 ,
,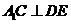 .
.
又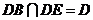 ,
,
所以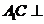 平面
平面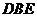 .································································································ 6分
.································································································ 6分
(Ⅱ)设向量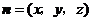 是平面
是平面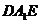 的法向量,则
的法向量,则
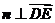 ,
,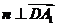 .
.
故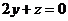 ,
,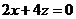 .
.
令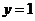 ,则
,则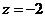 ,
,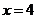 ,
,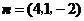 .······························································· 9分
.······························································· 9分
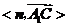 等于二面角
等于二面角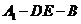 的平面角,
的平面角,
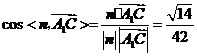 .
.
所以二面角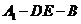 的大小为
的大小为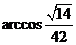 .·························································· 12分
.·························································· 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com