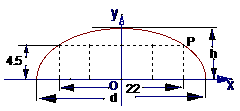
6、(1)解：如下图建立直角坐标系，则点P(11，45)，

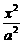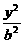椭圆方程为+=1

将b=h=6与点P坐标代入椭圆方程，得

a=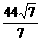，此时l=2a=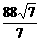≈333

因此隧道的拱宽约为333 m

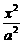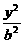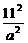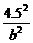(2)解法一：由椭圆方程+=1，得+=1

因为+≥，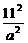

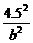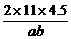即ab≥99，且l=2a，h=b，所以S=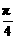lh=≥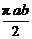

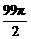
当S取最小值时，有==，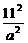

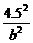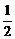得a=11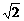，b=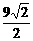

此时l=2a=22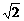≈311，h=b≈64

故当拱高约为64 m、拱宽约为311 m时，土方工程量最小

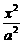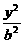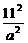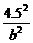解法二：由椭圆方程+=1，得+=1

于是b²=·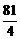

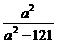
a²b²=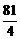(a²－121+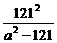+24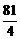2)≥(2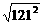+242)=81×121，

即ab≥99，当S取最小值时，

有a²－121=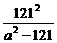

得a=11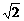，b=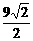，以下同解法一

5、解：(1)如下图，在反光镜的轴截面内建立直角坐标系，使反光镜的顶点(即抛物线的顶点)与原点重合，x轴垂直于镜口直径.

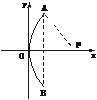
由已知，得A点坐标是(2，6)，

设抛物线方程为y²=2px(p＞0)，

则36=2p×2，p=9.

所以所求抛物线的标准方程是y²=18x，

焦点坐标是F(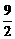，0).

(2)∵盛水的容器在焦点处，∴A、F两点间的距离即为每根铁筋长.

|AF|=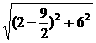=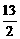(或|AF|=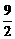+2=).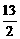

故每根铁筋的长度是6.5 m.

8.(2006上海春)学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如图：航天器运行(按顺时针方向)的轨迹方程为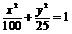，变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以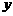轴为对称轴、 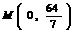为顶点的抛物线的实线部分，降落点为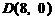. 观测点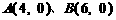同时跟踪航天器.

(1)求航天器变轨后的运行轨迹所在的曲线方程；

(2)试问：当航天器在轴上方时，观测点测得离航天器的距离分别为多少时，应向航天器发出变轨指令？

AC　 3、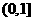　 4、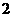　

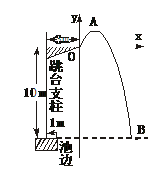
7.中国跳水运动员进行10 m跳台跳水训练时，身体(看成一点)在空中的运动路线为如下图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).

在跳某个规定动作时，正常情况下，该运动员在空中的最高处距水面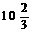 m，入水处距池边的距离为4 m，同时，运动员在距水面高度为5 m或5 m以上时，必须完成规定的翻腾动作，并调整好入水姿势，否则就会出现失误.

(1)求这条抛物线的解析式；

(2)在某次试跳中，测得运动员在空中的运动路线是(1)中的抛物线，且运动员在空中调整好入水姿势时，距池边的水平距离为3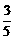m，问此次跳水会不会失误？并通过计算说明理由；

(3)要使此次跳水不至于失误，该运动员按(1)中抛物线运行，且运动员在空中调整好入水姿势时，距池边的水平距离至多应为多少？

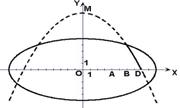
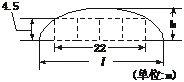
6.如下图，某隧道设计为双向四车道，车道总宽22 m，要求通行车辆限高4.5 m，隧道全长2.5 km，隧道的拱线近似地看成半个椭圆形状

(1)若最大拱高h为6 m，则隧道设计的拱宽l是多少？

(2)若最大拱高h不小于6 m，则应如何设计拱高h和拱宽l，才能使半个椭圆形隧道的土方工程量最小？

　 (半个椭圆的面积公式为S=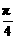lh，柱体体积为底面积乘以高.本题结果均精确到0.1 m)

5.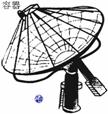下图是一种加热水和食物的太阳灶，上面装有可旋转的抛物面形的反光镜，镜的轴截面是抛物线的一部分，盛水和食物的容器放在抛物线的焦点处，容器由若干根等长的铁筋焊接在一起的架子支撑已知镜口圆的直径为12 m，镜深2 m..

(1)建立适当的坐标系，求抛物线的方程和焦点的位置；

(2)若把盛水和食物的容器近似地看作点，试求每根铁筋的长度

4.河上有一抛物线型拱桥，当水面距拱顶5 m时，水面宽为8 m，一小船宽4 m，高2 m，载货后船露出水面上的部分高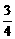 m，问水面上涨到与抛物线拱顶相距___________m时，小船不能通航.

3.一个酒杯的轴截面是抛物线的一部分，它的方程是x²=2y(0≤y≤20).在杯内放入一个玻璃球，要使球触及酒杯底部，则玻璃球的半径r的范围为____________.

1.1998年12月19日，太原卫星发射中心为摩托罗拉公司(美国)发射了两颗“铱星”系统通信卫星.卫星运行的轨道是以地球中心为一个焦点的椭圆，近地点为m km，远地点为　 n km，地球的半径为R km，则通信卫星运行轨道的短轴长等于

A.2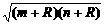　　　 B. 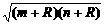　　　C.2mn　　　 D.mn

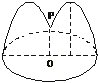　 2.如下图，花坛水池中央有一喷泉，水管OP=1 m，水从喷头P喷出后呈抛物线状先向上至最高点后落下，若最高点距水面2 m，P距抛物线对称轴1 m，则在水池直径的下列可选值中，最合算的是

A.2.5 m　　　　　　　　　　　　　　　　　 B.4 m

C.5 m　　　　　　　　　　　　　　　　　　 D.6 m　　　　　　　　　

9、解　 (1)∵点F₂关于l的对称点为Q，连接PQ，

∴∠F₂PR=∠QPR，|F₂R|=|QR|，|PQ|=|PF₂|

又因为l为∠F₁PF₂外角的平分线，故点F₁、P、Q在同一直线上，设存在R(x₀,y₀),Q(x₁,y₁),F₁(－c,0),F₂(c,0)　

|F₁Q|=|F₂P|+|PQ|=|F₁P|+|PF₂|=2a,则(x₁+c)²+y₁²=(2a)²　

又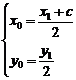

得x₁=2x₀－c,y₁=2y₀　

∴(2x₀)²+(2y₀)²=(2a)²，∴x₀²+y₀²=a²　

故R的轨迹方程为　 x²+y²=a²(y≠0)

(2)如右图，∵S_△AOB=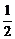|OA|·|OB|·sinAOB=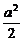sinAOB

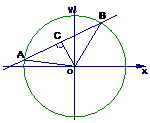当∠AOB=90°时，S_△AOB最大值为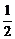a²　

此时弦心距|OC|=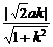　

在Rt△AOC中，∠AOC=45°，