16．设a>0，a≠1，f(x)=log_a(x+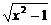)(x≥1)．

(1)求f(x)的反函数f^-1(x)及其定义域；

(2)设b_n=f^-1(n),S_n=b₁+b₂+…+b_n,试求证当|log₂a|<1时，对于n∈N*，有S_n＜2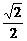ⁿ-()ⁿ.

15．△ABC中，内角A、B、C成等比数列，且b²-a²=ac，求A、B、C.

14．某企业2003年的纯利润为500万元，因设备老化等原因，企业的生产能力将逐年下降.若不进行技术改造，预测从今年起每年比上一年纯利润减少20万元.今年初该企业一次性投入资金600万元进行技术改造，预测在未扣除技术改造资金的情况下，第n年(今

年为第一年)的利润为500(1+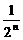)万元(n为正整数).

(1)设从今年起的前n年，若该企业不进行技术改造的累计纯利润为A_n万元，进行技术改造后的累计纯利润为B_n万元(须扣除技术改造资金)，求A_n,B_n的表达式;

(2)依上述预测，从今年起该企业至少经过多少年，进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润？

13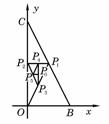．如图，△OBC的三个顶点坐标分别为(0,0)、(1，0)、(0，2)，

设P₁为线段BC的中点，P₂为线段CO的中点，P₃为线段OP₁的

中点，对于每一个正整数n,P_n+3为线段P_nP_n+1的中点，令P_n的坐

标为(x_n,y_n)，a_n=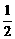y_n+y_n+1+y_n+2.

(2)证明y_n+4=1-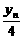,n∈N*;

(3)若记b_n=y_4n+4-y_4n,n∈N*,证明{b_n}是等比数列.

12．有一堆物品，某层放n²个，而它的上一层比它少放(2n-1)个(n≥2),已知这堆物品底层放100个，顶层放16个，这堆物品共有　　　　 个.

11．大楼共n层(n为奇数)，现每层指定一人，共n人集中到第k层开会，要使n位参会

人员上、下楼梯所走路程总和最短(假定相邻两层楼梯长相等，为a)，则k=　　　　　 .

10．已知f(x)为一次函数，若f(3)=15,且f(2)、f(5)、f(14)成等比数列，则f(1)+f(2)+…

+f(n)=　　　　　 .

9．若A、B、C成等差数列，则直线Ax+By+C=0，必过点　　　　　 .

8．一个正数组成的等比数列前7项之和是2，其后14项之和是12，则再后面21项之和

是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A.110　　　　 B.108　　　　 C.104　　　　 D.112

7．已知{a_n}是首项为50，公差为2的等差数列，{b_n}是首项为10，公差为4的等差数列.设以a_k，b_k为相邻两边的矩形内最大圆的面积为S_k，若k≤21，那么S_k等于　 (　　 )

A.π(2k+1)²　　 B.π(k+12)² 　　　C.π(2k+3)²　　 D.π(k+24)²