
题目列表(包括答案和解析)
3.(福建9) 某班级要从4名男士、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为( A )
A.14 B.24 C.28 D.48
2.(安徽12)12名同学合影,站成前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的总数是 ( C )
A. 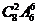 B.
B. 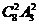 C.
C.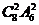 D.
D.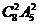
1.(安徽7).设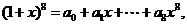 则
则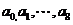 中奇数的个数为( A )
中奇数的个数为( A )
A.2 B.3 C.4 D.5
18.(陕西20)(本小题满分12分)
已知数列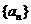 的首项
的首项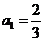 ,
,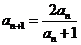 ,
,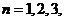 ….
….
(Ⅰ)证明:数列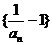 是等比数列;
是等比数列;
(Ⅱ)数列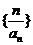 的前
的前 项和
项和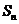 .
.
解:(Ⅰ)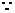
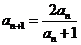 ,
,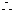
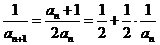 ,
,
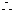
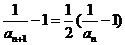 ,又
,又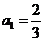 ,
,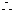
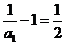 ,
,
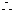 数列
数列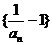 是以为
是以为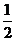 首项,
首项,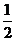 为公比的等比数列.
为公比的等比数列.
(Ⅱ)由(Ⅰ)知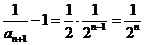 ,即
,即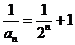 ,
,
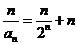 .
.
设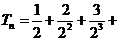 …
…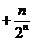 , ①
, ①
则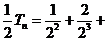 …
… ,②
,②
由① ②得
②得
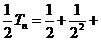 …
…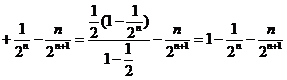 ,
,
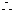
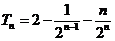 .又
.又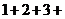 …
…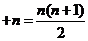 .
.
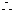 数列
数列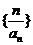 的前
的前 项和
项和 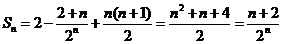 .
.
17.(湖北21).(本小题满分14分)
已知数列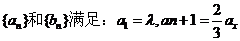
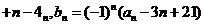 ,其中
,其中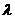 为实数,
为实数, 为正整数.
为正整数.
(Ⅰ)证明:当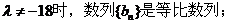
(Ⅱ)设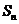 为数列
为数列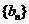 的前n项和,是否存在实数
的前n项和,是否存在实数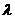 ,使得对任意正整数n,都有
,使得对任意正整数n,都有
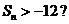 若存在,求
若存在,求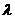 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(Ⅰ)证明:假设存在一个实数l,使{an}是等比数列,则有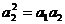 ,即
,即
(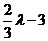 )2=
)2= 2
2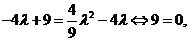 矛盾.
矛盾.
所以{an}不是等比数列.
(Ⅱ)证明:∵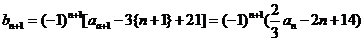



 又
又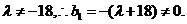 由上式知
由上式知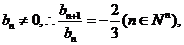
 故当
故当 数列{bn}是以
数列{bn}是以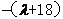 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.
(Ⅲ)当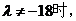 由(Ⅱ)得
由(Ⅱ)得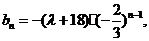 于是
于是

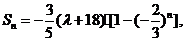
当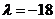 时,
时,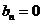 ,从而
,从而 上式仍成立.
上式仍成立.
要使对任意正整数n , 都有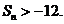
即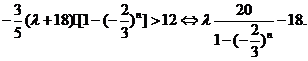
令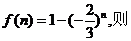
当n为正奇数时,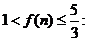 当n为正偶数时,
当n为正偶数时,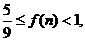

于是可得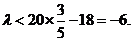
综上所述,存在实数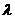 ,使得对任意正整数
,使得对任意正整数 ,都有
,都有

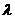 的取值范围为
的取值范围为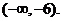
16.(重庆22)(本小题满分12分,(Ⅰ)小问6分.(Ⅱ)小问6分)
设各项均为正数的数列{an}满足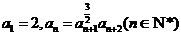 .
.
(Ⅰ)若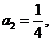 求a3,a4,并猜想a2008的值(不需证明);
求a3,a4,并猜想a2008的值(不需证明);
(Ⅱ)若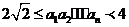 对n≥2恒成立,求a2的值.
对n≥2恒成立,求a2的值.
解:(I)因a1=2,a2=2-2,故


由此有a1=2(-2)0, a2=2(-2)4, a3=2(-2)2, a4=2(-2)3,
从而猜想an的通项为
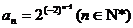 ,
,
所以a2xn=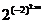 .
.
(Ⅱ)令xn=log2an.则a2=2x2,故只需求x2的值。
设Sn表示x2的前n项和,则a1a2…an=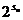 ,由2
,由2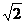 ≤a1a2…an<4得
≤a1a2…an<4得
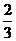 ≤Sn=x1+x2+…+xn<2(n≥2).
≤Sn=x1+x2+…+xn<2(n≥2).
因上式对n=2成立,可得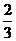 ≤x1+x2,又由a1=2,得x1=1,故x2≥
≤x1+x2,又由a1=2,得x1=1,故x2≥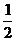 .
.
由于a1=2,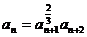 (n∈N*),得
(n∈N*),得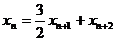 (n∈N*),即
(n∈N*),即
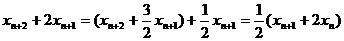 ,
,
因此数列{xn+1+2xn}是首项为x2+2,公比为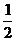 的等比数列,故
的等比数列,故
xn+1+2xn=(x2+2)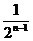 (n∈N*).
(n∈N*).
将上式对n求和得
Sn+1-x1+2Sn=(x2+2)(1+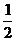 +…+
+…+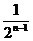 )=(x2+2)(2-
)=(x2+2)(2-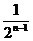 )(n≥2).
)(n≥2).
因Sn<2,Sn+1<2(n≥2)且x1=1,故
(x2+2)(2-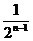 )<5(n≥2).
)<5(n≥2).
因此2x2-1<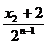 (n≥2).
(n≥2).
下证x2≤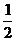 ,若淆,假设x2>
,若淆,假设x2>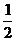 ,则由上式知,不等式
,则由上式知,不等式
2n-1<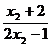
对n≥2恒成立,但这是不可能的,因此x2≤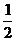 .
.
又x2≥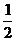 ,故z2=
,故z2=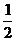 ,所以a2=2
,所以a2=2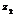 =
=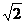 .
.
15.(浙江18)(本题14分)已知数列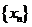 的首项
的首项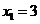 ,通项
,通项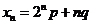 (
(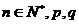 为常数),且
为常数),且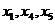 成等差数列,求:
成等差数列,求:
(Ⅰ)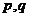 的值;
的值;
(Ⅱ)数列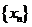 的前
的前 项的和
项的和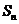 的公式。
的公式。
(Ⅰ)解:由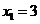 ,得
,得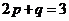 ,
,
又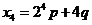 ,
, ,且
,且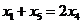 ,得
,得
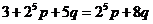 ,
,
解得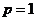 ,
,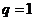 .
.
(Ⅱ)解: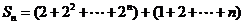
 .
.
14.(天津20)(本小题满分12分)
已知数列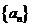 中,
中,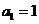 ,
,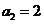 ,且
,且
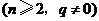 .
.
(Ⅰ)设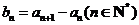 ,证明
,证明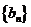 是等比数列;
是等比数列;
(Ⅱ)求数列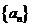 的通项公式;
的通项公式;
(Ⅲ)若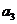 是
是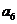 与
与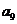 的等差中项,求
的等差中项,求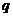 的值,并证明:对任意的
的值,并证明:对任意的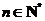 ,
,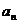 是
是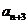 与
与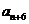 的等差中项.
的等差中项.
(Ⅰ)证明:由题设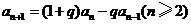 ,得
,得
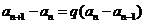 ,
,
即
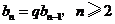 .
.
又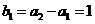 ,
,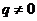 ,所以
,所以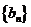 是首项为1,公比为
是首项为1,公比为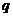 的等比数列.
的等比数列.
(Ⅱ)解:由(Ⅰ),
 ,
,
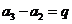 ,
,
……
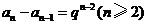 .
.
将以上各式相加,得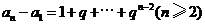 .所以当
.所以当 时,
时,
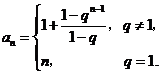
上式对 显然成立.
显然成立.
(Ⅲ)解:由(Ⅱ),当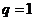 时,显然
时,显然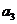 不是
不是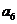 与
与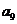 的等差中项,故
的等差中项,故 .
.
由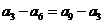 可得
可得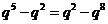 ,由
,由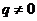 得
得
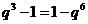 , ①
, ①
整理得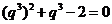 ,解得
,解得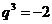 或
或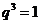 (舍去).于是
(舍去).于是
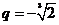 .
.
另一方面,
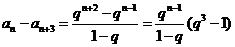 ,
,
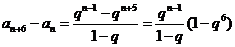 .
.
由①可得
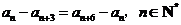 .
.
所以对任意的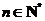 ,
,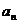 是
是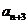 与
与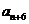 的等差中项.
的等差中项.
13.(四川21)(本小题满分12分)
设数列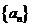 的前
的前 项和为
项和为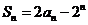 ,
,
(Ⅰ)求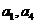
(Ⅱ)证明: 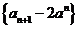 是等比数列;
是等比数列;
(Ⅲ)求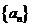 的通项公式
的通项公式
[解]:(Ⅰ)因为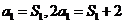 ,所以
,所以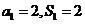
由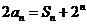 知
知
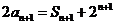

得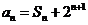 ①
①
所以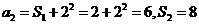
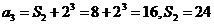
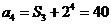
(Ⅱ)由题设和①式知
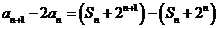

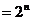
所以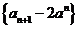 是首项为2,公比为2的等比数列。
是首项为2,公比为2的等比数列。
(Ⅲ)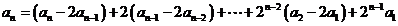
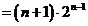
12.(上海21)(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知数列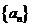 :
: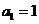 ,
,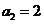 ,
, ,
,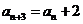 (
( 是正整数),与数列
是正整数),与数列
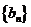 :
: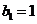 ,
,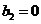 ,
,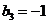 ,
,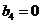 ,
,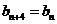 (
( 是正整数).
是正整数).
记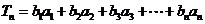 .
.
(1)若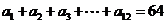 ,求
,求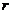 的值;
的值;
(2)求证:当 是正整数时,
是正整数时,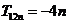 ;
;
(3)已知 ,且存在正整数
,且存在正整数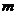 ,使得在
,使得在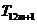 ,
, ,
,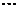 ,
, 中有4项为100.求
中有4项为100.求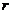 的值,并指出哪4项为100.
的值,并指出哪4项为100.
[解](1)
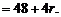 ………………..2分
………………..2分
∵ 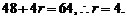 ………………..4分
………………..4分
[证明](2)用数学归纳法证明:当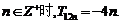
①
当n=1时,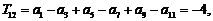 等式成立….6分
等式成立….6分
②
假设n=k时等式成立,即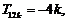
那么当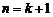 时,
时,
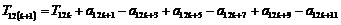 ………8分
………8分
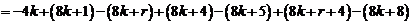
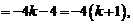 等式也成立.
等式也成立.
根据①和②可以断定:当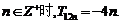 …………………...10分
…………………...10分
[解](3)
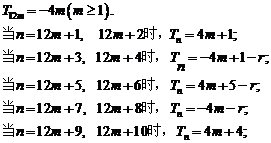
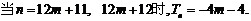 ………………………..13分
………………………..13分
∵ 4m+1是奇数,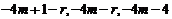 均为负数,
均为负数,
∴ 这些项均不可能取到100. ………………………..15分
此时,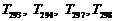 为100.
…………………………18分
为100.
…………………………18分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com