
题目列表(包括答案和解析)
5.若|a+b|=|a-b|,则向量a与b的关系是 ( )
A.a=0或b=0 B.|a|=|b| C.ab=0 D.以上都不对
4.若有点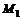 (4,3)和
(4,3)和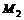 (2,-1),点M分有向线段
(2,-1),点M分有向线段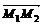 的比λ=-2,则点M的坐标为( )
的比λ=-2,则点M的坐标为( )
A.(0,-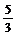 )
B.(6,7) C.(-2,-
)
B.(6,7) C.(-2,-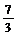 )
D.(0,-5)
)
D.(0,-5)
3.将函数y=sinx按向量a=(1,-1)平移后,所得函数的解析式是 ( )
A.y′=sin(x′-1)-1 B.y′=sin(x′+1)-1
C.y′=sin(x′+1)+1 D.y′=sin(x′-1)+1
2.若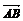 =3e,
=3e,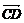 =-5e且|
=-5e且|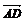 |=|
|=|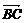 ,则四边形ABCD是 ( )
,则四边形ABCD是 ( )
A.平行四边形 B.菱形 C.等腰梯形 D.非等腰梯形
1.下列五个命题:①|a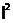 =
=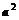 ;②
;②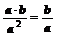 ;③
;③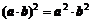 ;④
;④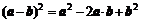 ;
;
⑤若a·b=0,则a=0或b=0.
其中正确命题的序号是 ( )
A.①②③ B.①④ C.①③④ D.②⑤
44.(江苏18)在平面直角坐标系 中,二次函数
中,二次函数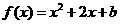 (
( )与两坐标轴有三
)与两坐标轴有三
个交点.记过三个交点的圆为圆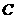 .
.
(Ⅰ)求实数b的取值范围;
(Ⅱ)求圆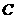 的方程;
的方程;
(Ⅲ)圆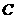 是否经过定点(与
是否经过定点(与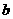 的取值无关)?证明你的结论.
的取值无关)?证明你的结论.
解:(Ⅰ)令x=0,得抛物线于y轴的交点是(0,b)
令f(x)=0,得x2+2x+b=0,由题意b≠0且△>0,解得b<1且b≠0
(Ⅱ)设所求圆的一般方程为x2+ y2+Dx+Ey+F=0
令y=0,得x2+Dx+F=0,这与x2+2x+b=0是同一个方程,故D=2,F=b
令x=0,得y2+ Ey+b=0,此方程有一个根为b,代入得E=-b-1
所以圆C的方程为x2+ y2+2x -(b+1)y+b=0
(Ⅲ)圆C必过定点(0,1),(-2,1)
证明如下:将(0,1)代入圆C的方程,得左边= 02+ 12+2×0-(b+1)×1+b=0,右边=0
所以圆C必过定点(0,1);
同理可证圆C必过定点(-2,1).
43.(宁夏海南文科第20题)
已知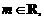 直线
直线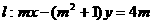 和圆
和圆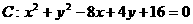 .
.
(Ⅰ)求直线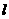 斜率的取值范围;
斜率的取值范围;
(Ⅱ)直线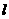 能否将圆
能否将圆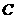 分割成弧长的比值为
分割成弧长的比值为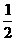 的两段圆弧?为什么?
的两段圆弧?为什么?
解:(Ⅰ)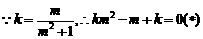 ,
,
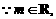 ∴当k≠0时
∴当k≠0时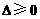 ,解得
,解得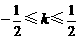 且k≠0
且k≠0
又当k=0时,m=0,方程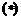 有解,所以,综上所述
有解,所以,综上所述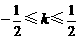
(Ⅱ)假设直线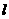 能否将圆
能否将圆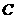 分割成弧长的比值为
分割成弧长的比值为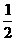 的两段圆弧.设直线
的两段圆弧.设直线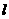 与圆
与圆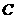 交于A,B两点
交于A,B两点
则∠ACB=120°.∵圆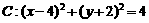 ,∴圆心C(4,-2)到l的距离为1.
,∴圆心C(4,-2)到l的距离为1.
故有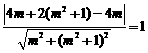 ,整理得
,整理得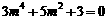 .
.
∵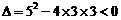 ,∴
,∴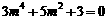 无实数解.
无实数解.
因此直线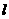 不可能将圆
不可能将圆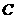 分割成弧长的比值为
分割成弧长的比值为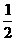 的两段圆弧.
的两段圆弧.
42.(四川文、理科14)已知直线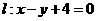 与圆
与圆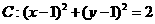 ,则
,则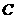 上各点到
上各点到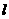 距离
距离
的最小值为 .
解析:由数想形,所求最小值=圆心到到直线的距离-圆的半径.圆心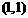 到直线
到直线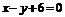 的距离
的距离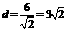 .故最小值为
.故最小值为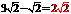 .
.
41.(湖南文科14)将圆x2+y2=1沿x轴正向平移1个单位后得到圆C,则圆C的方程是 ;
若过点(3,0)的直线l和圆C相切,则直线l的斜率是 .
答案:(x-1)2+y2=1;
40.(天津文科15)已知圆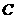 的圆心与点
的圆心与点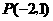 关于直线
关于直线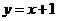 对称.直线
对称.直线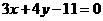 与
与
圆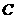 相交于
相交于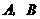 两点,且
两点,且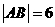 ,则圆
,则圆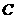 的方程为
.
的方程为
.
答案: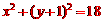
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com