
题目列表(包括答案和解析)
2. 若 则
则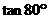 等于( )
等于( )
A. 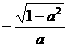 B.
B. 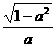 C.
C. 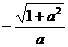 D.
D. 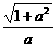
1. 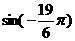 的值等于( )
的值等于( )
A. 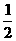 B.
B. 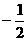 C.
C. 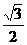 D.
D. 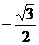
重点:运用诱导公式,把求任意角的三角函数值问题转化为求0°-90°间角的三角函数值的问题,任意角的三角函数。
难点:对诱导公式中符号的确定
[典型例题]
[例1] 设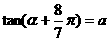 ,求
,求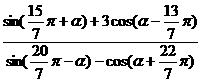 的值。
的值。
解:
方法一:
∵ 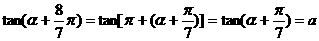
∴ 原式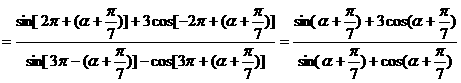
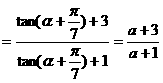
方法二:
原式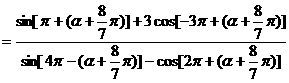
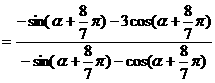
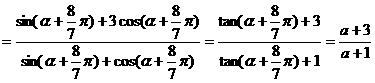
[例2] 设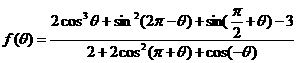 求
求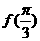 的值。
的值。
解: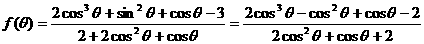
∵ 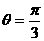 ∴
∴ 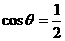 ∴
∴ 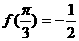
[例3] 已知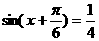 ,求
,求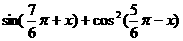 的值。
的值。
解:∵ 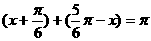 ∴
∴ 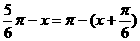
又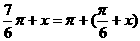
∴ 原式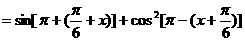
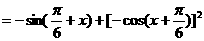
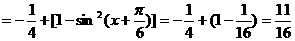
[例4] 已知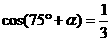 ,
,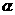 为第三象限角,求
为第三象限角,求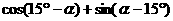 的值。
的值。
解: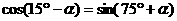 又 ∵
又 ∵ 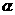 是第三象限角,
是第三象限角,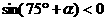
∴ 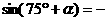
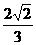 ∴
∴ 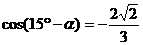
∵ 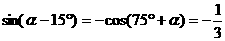
∴ 原式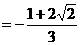
[例5] 已知 ,
, 是关于x的方程
是关于x的方程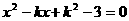 的两实根,且
的两实根,且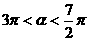 ,求
,求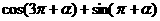 的值。
的值。
解:∵  ,
, 是方程
是方程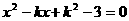 的两实根
的两实根
∴ 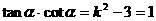 ∴
∴ 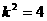
∵ 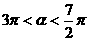 ∴
∴ 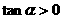 ,
,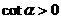 ,
,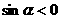 ,
,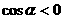
∴ 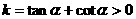 ∴
∴ 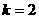 ∴ 方程化为
∴ 方程化为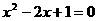
∴ 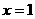 即
即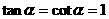 ∴
∴ 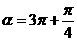
∴ 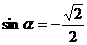 ,
,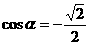
∴ 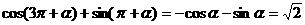
[例6] 已知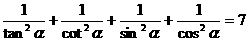 ,求
,求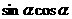 的值。
的值。
解:由已知等式变形可得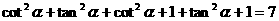
即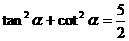 ∴
∴ 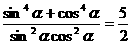
∴ 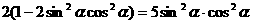 ∴
∴ 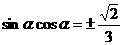
[例7] 已知: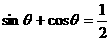 ,求
,求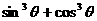 和
和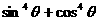 的值。
的值。
解:由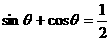 平方,可得
平方,可得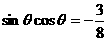
∴ 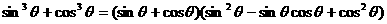
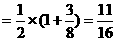
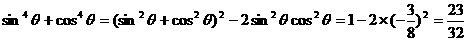
[例8] 已知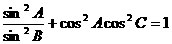 ,求证:
,求证: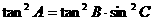
证:由已知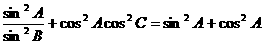
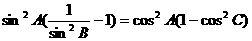
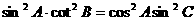
∴ 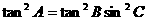
[模拟试题]
正弦、余弦的诱导公式;任意角的三角函数习题课
3.
解:(I) ∵x>0,∴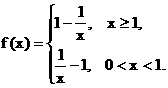
∴f(x)在(0,1)上为减函数,在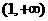 上是增函数.
上是增函数.
由0<a<b,且f(a)=f(b),
可得 0<a 1<b和
1<b和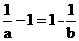 .
.
即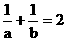 .
.
∴2ab=a+b>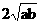 .
.
故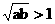 ,即ab>1.
,即ab>1.
(II)不存在满足条件的实数a,b.
若存在满足条件的实数a,b,使得函数y=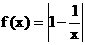 的定义域、值域都是
的定义域、值域都是
[a,b],则a>0.
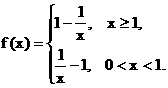
① 当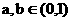 时,
时,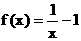 在(0,1)上为减函数.
在(0,1)上为减函数.
故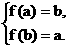 即
即 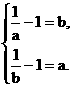
解得 a=b.
故此时不存在适合条件的实数a,b.
② 当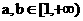 时,
时,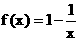 在
在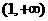 上是增函数.
上是增函数.
故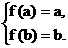 即
即 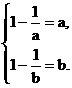
此时a,b是方程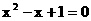 的根,此方程无实根.
的根,此方程无实根.
故此时不存在适合条件的实数a,b.
③ 当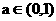 ,
,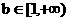 时,
时,
由于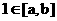 ,而
,而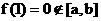 ,
,
故此时不存在适合条件的实数a,b.
综上可知,不存在适合条件的实数a,b.
(III)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb].
则a>0,m>0.
① 当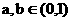 时,由于f(x)在(0,1)上是减函数,故
时,由于f(x)在(0,1)上是减函数,故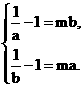 .此时刻得a,b异号,不符合题意,所以a,b不存在.
.此时刻得a,b异号,不符合题意,所以a,b不存在.
② 当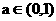 或
或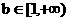 时,由(II)知0在值域内,值域不可能是[ma,mb],所以a,b不存在.
时,由(II)知0在值域内,值域不可能是[ma,mb],所以a,b不存在.
故只有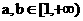 .
.
∵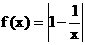 在
在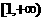 上是增函数,
上是增函数,
∴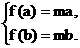 即
即 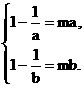
a, b是方程 的两个根.
的两个根.
即关于x的方程 有两个大于1的实根.
有两个大于1的实根.
设这两个根为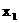 ,
,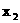 .
.
则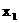 +
+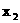 =
=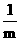 ,
,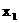 ·
·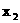 =
=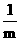 .
.
∴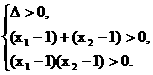 即
即 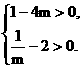
解得 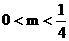 .
.
故m的取值范围是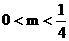 .
.
2.
解法一:(1)令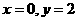 ,得:
,得: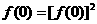

(2)任取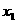 、
、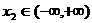 ,且
,且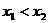 . 设
. 设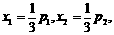 则
则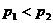
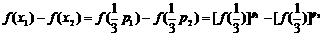
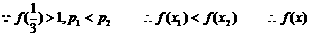 在R上是单调增函数
在R上是单调增函数
(3)由(1)(2)知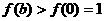
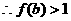
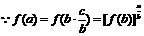
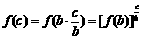
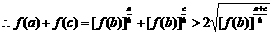
而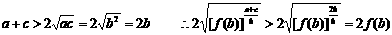
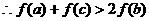 ……………………14分
……………………14分
解法二:(1)∵对任意x、y∈R,有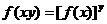
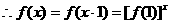 ∴当
∴当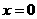 时
时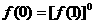
∵任意x∈R, 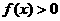

(2)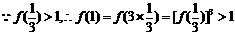
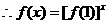 是R上单调增函数 即
是R上单调增函数 即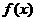 是R上单调增函数;
是R上单调增函数;
(3)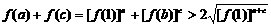
而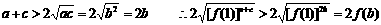
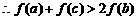
1.
解:(I)当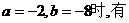
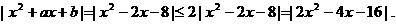
(II)在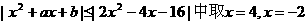
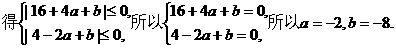
因此满足题意的实数a,b只能是a=-2, b=-8.
(III)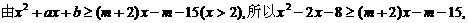
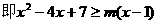 .
.
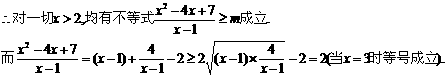
∴实数m的取值范围是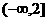 .
.
3.
已知函数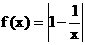
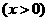 .
.
⑴ 当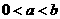 ,且
,且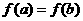 时,求证:
时,求证: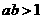 ;
;
⑵ 是否存在实数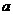 、
、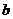
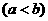 ,使得函数
,使得函数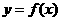 的定义域、值域都是
的定义域、值域都是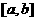 ,若存在,则求出
,若存在,则求出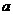 、
、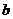 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
⑶ 若存在实数数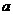 、
、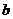
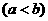 ,使得函数
,使得函数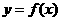 的定义域为
的定义域为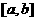 时,值域为
时,值域为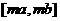
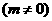 ,求
,求 的取值范围.
的取值范围.
2.
函数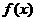 的定义域为
的定义域为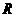 ,并满足以下条件:
,并满足以下条件:
① 对任意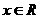 ,有
,有 ;
;
② 对任意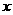 ,
,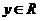 ,有
,有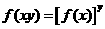 ;
;
③ 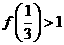 .
.
⑴ 求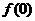 的值;
的值;
⑵ 求证: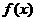 在
在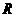 上是单调增函数;
上是单调增函数;
⑶ 若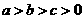 ,且
,且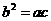 ,求证:
,求证: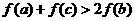 .
.
1.
已知实数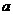 、
、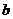 满足:关于x的不等式
满足:关于x的不等式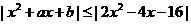 对一切
对一切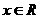 均成立.
均成立.
⑴ 请验证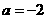 ,
,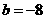 满足题意;
满足题意;
⑵ 求出所有满足题意的实数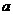 、
、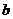 ,并说明理由;
,并说明理由;
⑶ 若对一切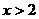 ,均有不等式
,均有不等式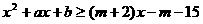 成立,求实数m的取值范围.
成立,求实数m的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com