
题目列表(包括答案和解析)
2.(本小题满分12分)
设A、B是椭圆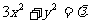 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(Ⅰ)确定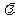 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的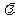 ,使得A、B、C、D四点在同一个圆上?并说明理由.
,使得A、B、C、D四点在同一个圆上?并说明理由.
(此题不要求在答题卡上画图)
本小题主要考查直线、圆和椭圆等平面解析几何的基础知识以及推理运算能力和综合解决问题的能力.
(Ⅰ)解法1:依题意,可设直线AB的方程为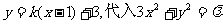 ,整理得
,整理得 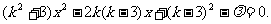 ①
①
设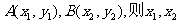 是方程①的两个不同的根,
是方程①的两个不同的根,
∴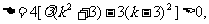 ②
②
且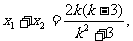 由N(1,3)是线段AB的中点,得
由N(1,3)是线段AB的中点,得
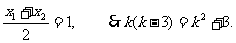
解得k=-1,代入②得,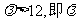 的取值范围是(12,+∞).
的取值范围是(12,+∞).
于是,直线AB的方程为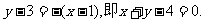
解法2:设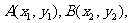 则有
则有
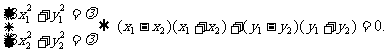
依题意,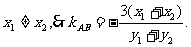
∵N(1,3)是AB的中点, ∴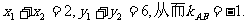
又由N(1,3)在椭圆内,∴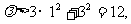
∴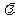 的取值范围是(12,+∞).
的取值范围是(12,+∞).
直线AB的方程为y-3=-(x-1),即x+y-4=0.
(Ⅱ)解法1:∵CD垂直平分AB,∴直线CD的方程为y-3=x-1,即x-y+2=0,
代入椭圆方程,整理得 
又设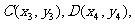 CD的中点为
CD的中点为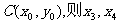 是方程③的两根,
是方程③的两根,
∴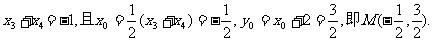
于是由弦长公式可得 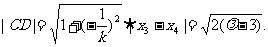 ④
④
将直线AB的方程x+y-4=0,代入椭圆方程得 ⑤
⑤
同理可得 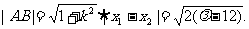 ⑥
⑥
∵当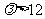 时,
时,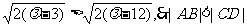
假设存在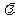 >12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.
>12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.
点M到直线AB的距离为
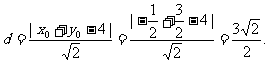 ⑦
⑦
于是,由④、⑥、⑦式和勾股定理可得
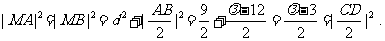
故当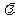 >12时,A、B、C、D四点匀在以M为圆心,
>12时,A、B、C、D四点匀在以M为圆心,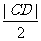 为半径的圆上.
为半径的圆上.
(注:上述解法中最后一步可按如下解法获得:)
A、B、C、D共圆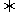 △ACD为直角三角形,A为直角
△ACD为直角三角形,A为直角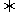 |AN|2=|CN|·|DN|,
|AN|2=|CN|·|DN|,
即 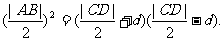 ⑧
⑧
由⑥式知,⑧式左边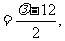
由④和⑦知,⑧式右边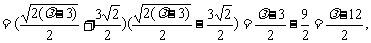
∴⑧式成立,即A、B、C、D四点共圆.
解法2:由(Ⅱ)解法1及λ>12,
∵CD垂直平分AB, ∴直线CD方程为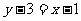 ,代入椭圆方程,整理得
,代入椭圆方程,整理得
 ③
③
将直线AB的方程x+y-4=0,代入椭圆方程,整理得
 ⑤
⑤
解③和⑤式可得 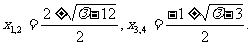
不妨设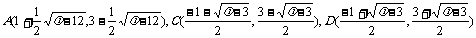
∴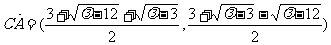
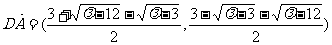
计算可得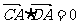 ,∴A在以CD为直径的圆上.
,∴A在以CD为直径的圆上.
又B为A关于CD的对称点,∴A、B、C、D四点共圆.
(注:也可用勾股定理证明AC⊥AD)
1.(本小题满分14分)
如图,设抛物线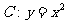 的焦点为F,动点P在直线
的焦点为F,动点P在直线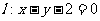 上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
(1)求△APB的重心G的轨迹方程.
(2)证明∠PFA=∠PFB.
解:(1)设切点A、B坐标分别为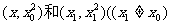 ,
,
∴切线AP的方程为:
切线BP的方程为: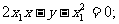
解得P点的坐标为: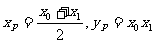
所以△APB的重心G的坐标为
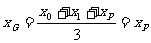 ,
,
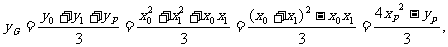
所以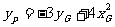 ,由点P在直线l上运动,从而得到重心G的轨迹方程为:
,由点P在直线l上运动,从而得到重心G的轨迹方程为:
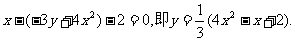
(2)方法1:因为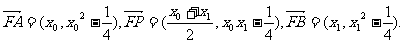
由于P点在抛物线外,则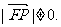
∴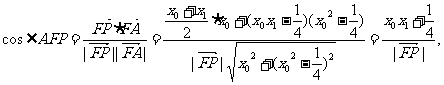
同理有
∴∠AFP=∠PFB.
方法2:①当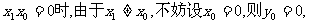 所以P点坐标为
所以P点坐标为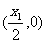 ,则P点到直线AF的距离为:
,则P点到直线AF的距离为:
即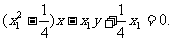
所以P点到直线BF的距离为: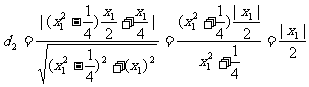
所以d1=d2,即得∠AFP=∠PFB.
②当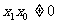 时,直线AF的方程:
时,直线AF的方程: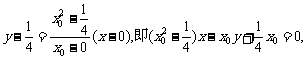
直线BF的方程:
所以P点到直线AF的距离为:
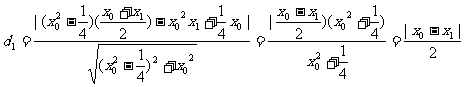 ,同理可得到P点到直线BF的距离
,同理可得到P点到直线BF的距离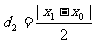 ,因此由d1=d2,可得到∠AFP=∠PFB.
,因此由d1=d2,可得到∠AFP=∠PFB.
22、某“帆板”集训队在一海滨区域进行集训,该海滨区域的海浪高度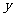 (米)随着时间
(米)随着时间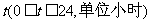 而周期性变化,每天各时刻
而周期性变化,每天各时刻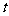 的浪高数据的平均值如下表:
的浪高数据的平均值如下表:
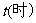 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
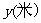 |
1.0 |
1.4 |
1.0 |
0.6 |
1.0 |
1.4 |
0.9 |
0.5 |
1.0 |
(Ⅰ)试画出散点图;
(Ⅱ)观察散点图,从 中选择一个合适的函数模型,并求出该拟合模型的解析式;
中选择一个合适的函数模型,并求出该拟合模型的解析式;
(Ⅲ)如果确定在白天7时~19时当浪高不低于0。8米时才进行训练,试安排恰当的训练时间。
21、已知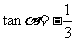 ,
,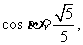
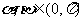
(1)求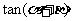 的值;
的值;
(2)求函数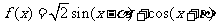 的最大值.
的最大值.
20、已知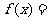
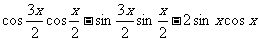 ,
,
(Ⅰ)求函数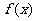 的最小正周期;(Ⅱ) 当
的最小正周期;(Ⅱ) 当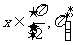 ,求函数
,求函数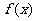 的零点.
的零点.
19、已知函数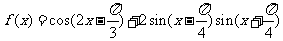
(Ⅰ)求函数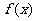 的最小正周期和图象的对称轴方程
的最小正周期和图象的对称轴方程
(Ⅱ)求函数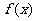 在区间
在区间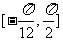 上的值域
上的值域
18、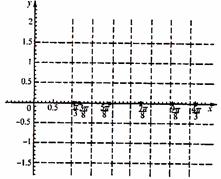 已知函数
已知函数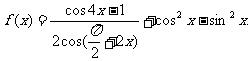
(Ⅰ)求函数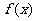 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(Ⅱ)在所给坐标系中画出函数在区间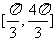 的图象
的图象
(只作图不写过程).
17、在△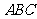 中,角
中,角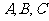 所对的边分别为
所对的边分别为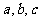 ,已知
,已知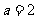 ,
,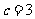 ,
,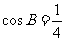 .(1)求
.(1)求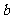 的值;(2)求
的值;(2)求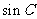 的值.
的值.
16、已知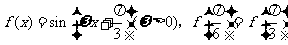 ,且
,且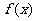 在区间
在区间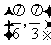 有最小值,无最大值,则
有最小值,无最大值,则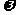 =__________.
=__________.
15、设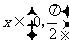 ,则函数
,则函数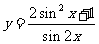 的最小值为
.
的最小值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com