
题目列表(包括答案和解析)
4.(1)a2=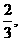
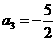
(2)a2n-2+1=a2n-2-2(2n-2)即a2n-1=a2n-2-2(2n-2)
a2n-1+1=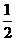 a2n-1+(2n-1)即a2n=
a2n-1+(2n-1)即a2n=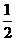 a2n-2-(2n-2)+(2n-1)
a2n-2-(2n-2)+(2n-1)
∴a2n-2=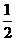 (a2n-2-2);
(a2n-2-2);
∴a2n=-(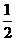 )n+2(n∈N*)
)n+2(n∈N*)
(3)∵当n=2k时,a2k+1=a2k-2×2k.(k=1,2,…,49)
∴叠加可得所有奇数项的和:
1-2×(2+4+…+98)+a2+a4+…+a98=(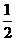 )49-4802
)49-4802
17.(Ⅰ)解:由已知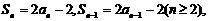
又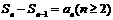 所以,
所以,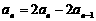 ,
,
所以,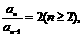 即数列
即数列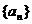 是等比数列.
是等比数列.
因为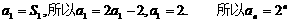
因为点P(bn,bn+1)在直线x-y+2=0上,所以bn-bn+1+2=0,
所以bn+1-bn=2,即数列{bn}是等差数列.
又,b1=1,所以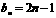
(Ⅱ)证明:由已知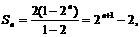
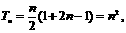
即证明不等式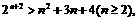
(1)当n=2时,2n+2=16,n2+3n+4=14,不等成立.
(2)假设当n=k时,不等式成立,即2k+2>k2+3k+4成立,
那么,当n=k+1时,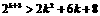 ,
,
以下只须证明 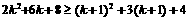 成立,
成立,
即只须证明k2+k≥0成立, 因为当k≥2时,k2+k≥0成立,
所以当n=k+1时,不等式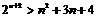 成立
成立
综合(1)(2),原不等式成立.
1.证明:(1)当n=1时,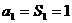
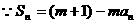 ①
① 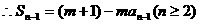 ②
②
①-②得: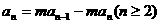
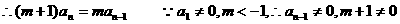
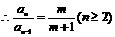
∴数列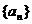 是首项为1,公比数
是首项为1,公比数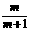 的等比数列.
的等比数列.
(2)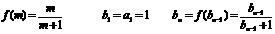
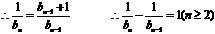
∴数列{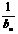 }是首项为1,公差为1的等差数列.
}是首项为1,公差为1的等差数列.
(3)由(2)得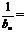 n 则
n 则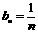
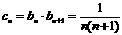
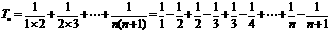
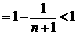
4.
已知数列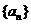 满足:
满足: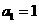 ,
,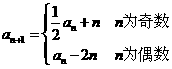 .
.
⑴ 求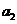 ,
,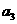 ;
;
⑵ 当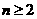 时,求
时,求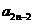 与
与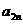 的关系式,并求数列
的关系式,并求数列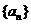 中偶数项的通项公式;
中偶数项的通项公式;
⑶ 数列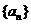 前100项中所有奇数项的和.
前100项中所有奇数项的和.
3.
已知数列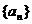 的前
的前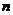 项和为
项和为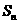 ,且
,且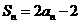
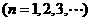 ,数列
,数列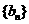
中,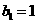 ,点
,点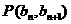 在直线
在直线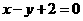 上.
上.
⑴ 求数列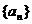 ,
,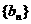 的通项
的通项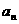 ,
,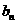 ;
;
⑵ 若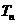 为数列
为数列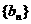 的前
的前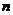 项和,证明:当
项和,证明:当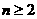 时,
时,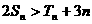 .
.
2.
已知等差数列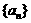 的前9项的和为153.
的前9项的和为153.
⑴ 数列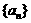 中是否存在确定的项,若存在,请求出该项,若不存在,请说明理由;
中是否存在确定的项,若存在,请求出该项,若不存在,请说明理由;
⑵ 若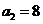 ,
,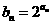 ,求数列
,求数列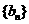 的前
的前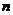 项的积
项的积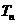 ;
;
⑶ 若从数列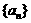 中,依次取出第二项、第四项、第八项、…、第
中,依次取出第二项、第四项、第八项、…、第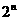 项,按原来的顺序组成新的数列
项,按原来的顺序组成新的数列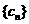 ,求数列
,求数列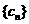 的前
的前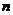 项的和
项的和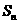 .
.
1.
数列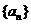 的前n项和为
的前n项和为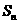
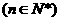 ,
,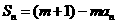 对于任意的
对于任意的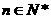 都成立,其中
都成立,其中 为常数,且
为常数,且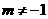 .
.
⑴ 求证:数列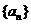 是等比数列;
是等比数列;
⑵ 记数列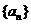 的公比为
的公比为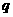 ,设
,设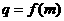 ,若数列
,若数列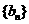 满足:
满足: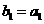 ,
,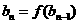
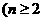 ,
,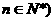 ,求证:
,求证: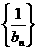 是等差数列;
是等差数列;
⑶ 在 ⑵ 的条件下,设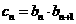 ,数列
,数列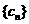 的前
的前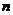 项和为
项和为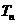 ,求证:
,求证: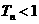 .
.
17.从52张(没有大小王)扑克牌中随机抽取5张,试求下列事件的概率:
(1)5张牌同一花色;
(2)恰有两张点数相同而另三张点数不同;
(3)恰好有两个两张点数相同而另一张是另外的点数;
(4)恰好有四张点数相同.
专题十 概率与统计
16.甲、乙两人各进行一次射击,若两人击中目标的概率均为0.6.求:
(1)两人均击中目标的概率;
(2)至少有1人击中目标的概翠.
15.已知8支球队中有3支弱队,以抽签的方式将这8支球队分为A、B两组,每组4支,求:
(1)A、B两组中有一组恰有两支弱队的概率;
(2)A组中至少有两支弱队的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com