
题目列表(包括答案和解析)
13.(江西理)18.(本小题满分12分)因冰雪灾害,某柑桔基地果林严重受损,为此有关专家提出两种拯救果树的方案,每种方案都需分两年实施.若实施方案一,预计第一年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4;第二年可以使柑桔产量为第一年产量的1.25倍、1.0倍的概率分别是0.5、0.5.若实施方案二,预计第一年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5;第二年可以使柑桔产量为第一年产量的1.2倍、1.0倍的概率分别是0.4、0.6.实施每种方案第一年与第二年相互独立,令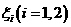 表示方案
表示方案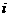 实施两年后柑桔产量达到灾前产量的倍数.
实施两年后柑桔产量达到灾前产量的倍数.
(1)写出ξ1、ξ2的分布列;
(2)实施哪种方案,两年后柑桔产量超过灾前产量的概率更大?
(3)不管哪种方案,如果实施两年后柑桔产量达不到、恰好达到、超过灾前产量,预计利润分别为10万元、15万元、20万元.问实施哪种方案的平均利润更大?
解:(1)ξ1的分布列为
|
ξ1 |
0.8 |
0.9 |
1 |
1.125 |
1.25 |
|
P1 |
0.2 |
0.15 |
0.35 |
0.15 |
0.15 |
ξ2的分布列为
|
ξ2 |
0.8 |
0.96 |
1 |
1.2 |
1.44 |
|
P2 |
0.3 |
0.2 |
0.18 |
0.24 |
0.08 |
(2)由(1)可得P1>1的概率P(P1>1)= 0.15 + 0.15 = 0.3,
P2>1的概率P(P2>1)= 0.24 + 0.08 = 0.32,
可见,P(P2>1)>P(P1>1)
∴实施方案2,两年后产量超过灾前概率更大。
(3)设实施方案1、2的平均利润分别为利润1、利润2,根据题意
利润1 = (0.2 +0.15)×10 + 0.35×15 + (0.15 + 0.15)×20
= 14.75(万元)
利润2 = (0.3 + 0.2)×10 + 0.18×15 + (0.24 + 0.08)×20
= 14.1(万元)
∴利润1>利润2,
∴实施方案1平均利润更大。
12.(湖南文)(16).(本小题满分12分)甲乙丙三人参加一家公司的招聘面试,面试合格者可正式签约。甲表示只要面试合格
就签约,乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约。设每人面试合格的概率都是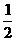 ,且面试是否合格互不影响。求:
,且面试是否合格互不影响。求:
(1)至少一人面试合格的概率;
(2)没有人签约的概率。
解:用A,B,C分别表示事件甲、乙、丙面试合格.由题意知A,B,C相互独立,
且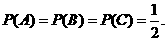
(1)至少有一人面试合格的概率是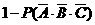
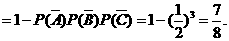
(2)没有人签约的概率为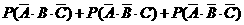
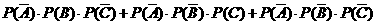
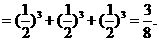
11.(湖南理)(16)(本小题满分12分)甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人面试合格的概率都是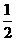 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率;
(2)签约人数 的分布列和数学期望.
的分布列和数学期望.
解 用A,B,C分别表示事件甲、乙、丙面试合格.由题意知A,B,C相互独立,且
P(A)=P(B)=P(C)=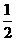 .
.
(1)至少有1人面试合格的概率是
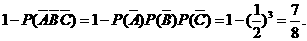
(2)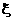 的可能取值为0,1,2,3.
的可能取值为0,1,2,3.
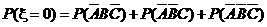
=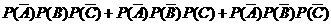
=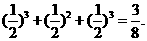
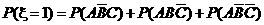
=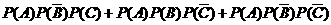
=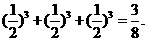
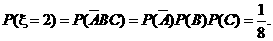
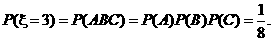
所以,
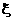 的分布列是
的分布列是
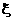 |
0 |
1 |
2 |
3 |
|
P |
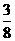 |
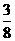 |
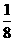 |
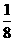 |
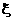 的期望
的期望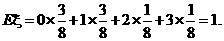
10.(湖北理)(17)(本小题满分12分)
袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4).现从袋中任取一球.ξ表示所取球的标号.
(1)求ξ的分布列,期望和方差;
(2)若η=aξ-b,Eη=1,Dη=11,试求a,b的值.
解:(1)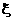 的分布列为:
的分布列为:
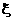 |
0 |
1 |
2 |
3 |
4 |
|
P |
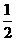 |
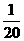 |
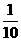 |
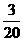 |
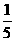 |
∴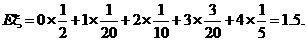
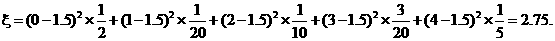 (2)由
(2)由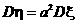 ,得a2×2.75=11,即
,得a2×2.75=11,即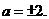 又
又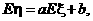 所以
所以
当a=2时,由1=2×1.5+b,得b=-2;
当a=-2时,由1=-2×1.5+b,得b=4.
∴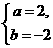 或
或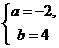 即为所求.
即为所求.
9.(海南宁夏文)(19).(本小题满分12分)为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查.6人得分情况如下:
5,6,7,8,9,10.
把这6名学生的得分看成一个总体.
(1)求该总体的平均数;
(2)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.
解:(1)总体平均数为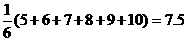 .
.
(2)设 表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”.
表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”.
从总体中抽取2个个体全部可能的基本结果有: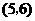 ,
,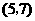 ,
,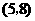 ,
,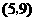 ,
,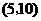 ,
,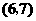 ,
,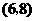 ,
,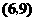 ,
,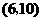 ,
,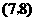 ,
,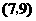 ,
,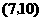 ,
,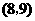 ,
,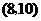 ,
,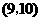 .
.
共15个基本结果.
事件 包括的基本结果有:
包括的基本结果有: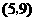 ,
,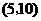 ,
,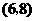 ,
,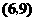 ,
,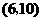 ,
,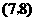 ,
,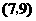 .
.
共有7个基本结果.
所以所求的概率为 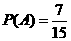 .
.
8.(海南宁夏理)(19).(本小题满分12分) 两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1和X2的分布列分别为
两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1和X2的分布列分别为
|
X1 |
5% |
10% |
|
P |
0.8 |
0.2 |
|
X2 |
2% |
8% |
12% |
|
P |
0.2 |
0.5 |
0.3 |
(1)在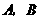 两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差DY1,DY2;
两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差DY1,DY2;
(2)将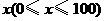 万元投资A项目,
万元投资A项目, 万元投资B项目,
万元投资B项目,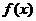 表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求
表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求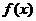 的最小值,并指出x为何值时,
的最小值,并指出x为何值时,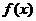 取到最小值.(注:
取到最小值.(注: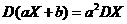 )
)
解:(1)由题设可知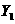 和
和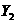 的分布列分别为
的分布列分别为
|
Y1 |
5 |
10 |
|
P |
0.8 |
0.2 |
|
Y2 |
2 |
8 |
12 |
|
P |
0.2 |
0.5 |
0.3 |
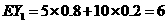 ,
,
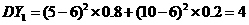 ,
,
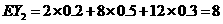 ,
,
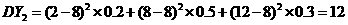 .
.
(2)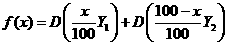
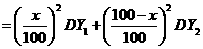
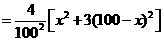
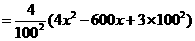 ,
,
当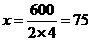 时,
时,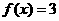 为最小值.
为最小值.
7.(广东文)(19).(本小题满分13分)某初级中学共有学生2000名,各年级男、女生人数如下表:
|
|
初一年级 |
初二年级 |
初三年级 |
|
女生 |
373 |
x |
y |
|
男生 |
377 |
370 |
z |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1) 求x的值;
(2) 现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)
已知y 245,z
245,z 245,求初三年级中女生比男生多的概率.
245,求初三年级中女生比男生多的概率.
解:(1)
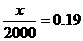

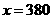
(2)初三年级人数为y+z=2000-(373+377+380+370)=500,
现用分层抽样的方法在全校抽取48名学生,应在初三年级抽取的人数为: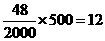 名
名
(3)设初三年级女生比男生多的事件为A ,初三年级女生男生数记为(y,z);
由(2)知 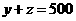 ,且
,且 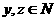 ,基本事件空间包含的基本事件有:
,基本事件空间包含的基本事件有:
(245,255)、(246,254)、(247,253)、……(255,245)共11个
事件A包含的基本事件有:(251,249)、(252,248)、(253,247)、(254,246)、(255,245) 共5个
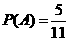
6.(广东理)(17).(本小题满分13分)随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为 .
.
(1)求 的分布列;(2)求1件产品的平均利润(即
的分布列;(2)求1件产品的平均利润(即 的数学期望);
的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为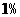 ,一等品率提高为
,一等品率提高为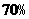 .如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
解: 的所有可能取值有6,2,1,-2;
的所有可能取值有6,2,1,-2;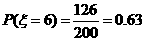 ,
,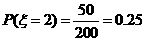
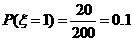 ,
,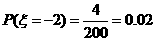
 |
6 |
2 |
1 |
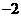 |
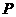 |
0.63 |
0.25 |
0.1 |
0.02 |
故 的分布列为:
的分布列为:
(2)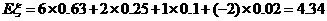
(3)设技术革新后的三等品率为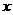 ,则此时1件产品的平均利润为
,则此时1件产品的平均利润为
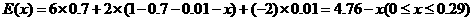
依题意,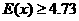 ,即
,即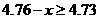 ,解得
,解得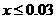 所以三等品率最多为
所以三等品率最多为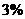
5.(福建文)(18)(本小题满分12分)三人独立破译同一份密码.已知三人各自破译出密码的概率分别为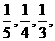 且他们是否破译出密码互不影响.
且他们是否破译出密码互不影响.
(1)求恰有二人破译出密码的概率;
(2)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.
解:记“第i个人破译出密码”为事件A1(i=1,2,3),依题意有
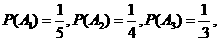 且A1,A2,A3相互独立.
且A1,A2,A3相互独立.
(1)设“恰好二人破译出密码”为事件B,则有
B=A1·A2· ·A1·
·A1·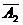 ·A3+
·A3+ ·A2·A3且A1·A2·
·A2·A3且A1·A2· ,A1·
,A1·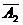 ·A3,
·A3, ·A2·A3
·A2·A3
彼此互斥
于是P(B)=P(A1·A2· )+P(A1·
)+P(A1·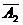 ·A3)+P(
·A3)+P( ·A2·A3)
·A2·A3)
=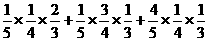 =
=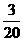 .
.
答:恰好二人破译出密码的概率为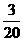 .
.
(2)设“密码被破译”为事件C,“密码未被破译”为事件D.
D= ·
·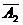 ·
· ,且
,且 ,
,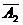 ,
, 互相独立,则有
互相独立,则有
P(D)=P( )·P(
)·P(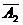 )·P(
)·P( )=
)=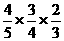 =
=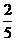 .
.
而P(C)=1-P(D)=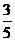 ,故P(C)>P(D).
,故P(C)>P(D).
答:密码被破译的概率比密码未被破译的概率大.
4.(福建理)(20)(本小题满分12分)
某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科 目B的考试.已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证 书.现某人参加这项考试,科目A每次考试成绩合格的概率均为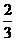 ,科目B每次考试 成绩合格的概率均为
,科目B每次考试 成绩合格的概率均为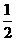 .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得证书的概率;
(2)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为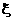 ,求
,求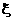 的数学期望E
的数学期望E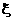 .
.
解:设“科目A第一次考试合格”为事件A,“科目A补考合格”为事件A2;“科目B第一次考试合格”为事件B,“科目B补考合格”为事件B.
(1)不需要补考就获得证书的事件为A1·B1,注意到A1与B1相互独立,
则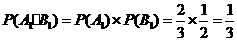 .
.
答:该考生不需要补考就获得证书的概率为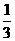 .
.
(2)由已知得, =2,3,4,注意到各事件之间的独立性与互斥性,可得
=2,3,4,注意到各事件之间的独立性与互斥性,可得
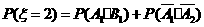
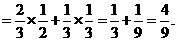
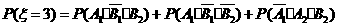
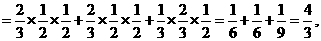
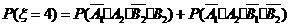
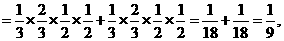
故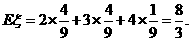
答:该考生参加考试次数的数学期望为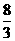 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com