
题目列表(包括答案和解析)
19. (本小题满分14分)
设双曲线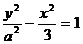 的两个焦点分别为
的两个焦点分别为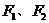 ,离心率为2.
,离心率为2.
(I)求此双曲线的渐近线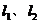 的方程;
的方程;
(II)若A、B分别为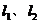 上的点,且
上的点,且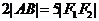 ,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线;
,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线;
(III)过点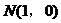 能否作出直线
能否作出直线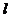 ,使
,使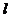 与双曲线交于P、Q两点,且
与双曲线交于P、Q两点,且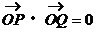 .若存在,求出直线
.若存在,求出直线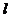 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
解:(I)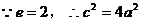
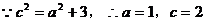
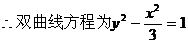 ,渐近线方程为
,渐近线方程为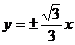 4分
4分
(II)设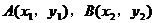 ,AB的中点
,AB的中点
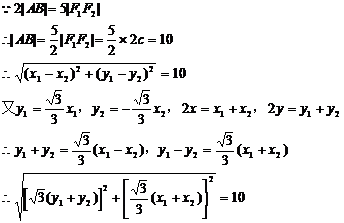
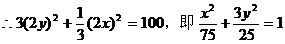
则M的轨迹是中心在原点,焦点在x轴上,长轴长为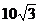 ,短轴长为
,短轴长为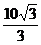 的椭圆.(9分)
的椭圆.(9分)
(III)假设存在满足条件的直线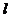
设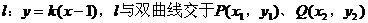
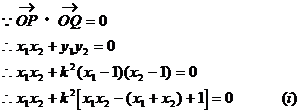
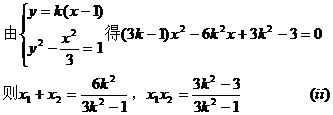
由(i)(ii)得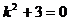
∴k不存在,即不存在满足条件的直线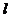 . 14分
. 14分
2.(本小题满分13分)
已知函数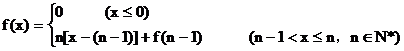 ,
,
数列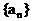 满足
满足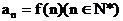
(I)求数列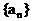 的通项公式;
的通项公式;
(II)设x轴、直线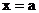 与函数
与函数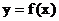 的图象所围成的封闭图形的面积为
的图象所围成的封闭图形的面积为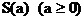 ,求
,求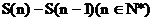 ;
;
(III)在集合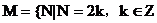 ,且
,且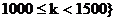 中,是否存在正整数N,使得不等式
中,是否存在正整数N,使得不等式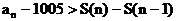 对一切
对一切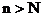 恒成立?若存在,则这样的正整数N共有多少个?并求出满足条件的最小的正整数N;若不存在,请说明理由.
恒成立?若存在,则这样的正整数N共有多少个?并求出满足条件的最小的正整数N;若不存在,请说明理由.
(IV)请构造一个与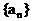 有关的数列
有关的数列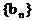 ,使得
,使得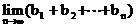 存在,并求出这个极限值.
存在,并求出这个极限值.
解:(I)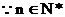
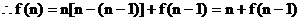
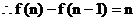 ……1分
……1分
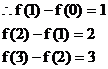
……
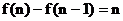
将这n个式子相加,得
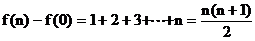
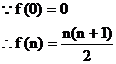
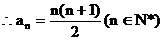 ……3分
……3分
(II)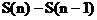 为一直角梯形(
为一直角梯形(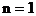 时为直角三角形)的面积,该梯形的两底边的长分别为
时为直角三角形)的面积,该梯形的两底边的长分别为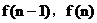 ,高为1
,高为1
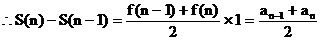
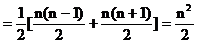 ……6分
……6分
(III)设满足条件的正整数N存在,则
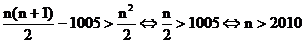
又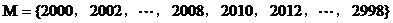
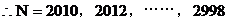 均满足条件
均满足条件
它们构成首项为2010,公差为2的等差数列.
设共有m个满足条件的正整数N,则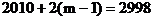 ,解得
,解得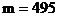
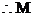 中满足条件的正整数N存在,共有495个,
中满足条件的正整数N存在,共有495个,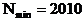 ……9分
……9分
(IV)设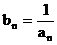 ,即
,即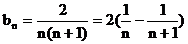
则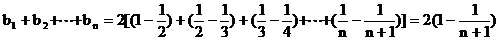
显然,其极限存在,并且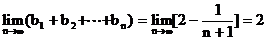 ……10分
……10分
注: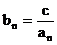 (c为非零常数),
(c为非零常数),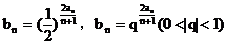 等都能使
等都能使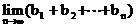 存在.
存在.
1.(本小题满分13分)
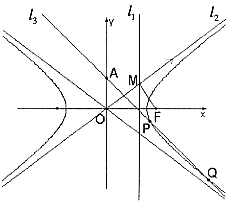 如图,已知双曲线C:
如图,已知双曲线C: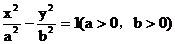 的右准线
的右准线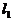 与一条渐近线
与一条渐近线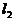 交于点M,F是双曲线C的右焦点,O为坐标原点.
交于点M,F是双曲线C的右焦点,O为坐标原点.
(I)求证: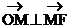 ;
;
(II)若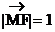 且双曲线C的离心率
且双曲线C的离心率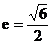 ,求双曲线C的方程;
,求双曲线C的方程;
(III)在(II)的条件下,直线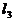 过点A(0,1)与双曲线C右支交于不同的两点P、Q且P在A、Q之间,满足
过点A(0,1)与双曲线C右支交于不同的两点P、Q且P在A、Q之间,满足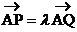 ,试判断
,试判断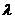 的范围,并用代数方法给出证明.
的范围,并用代数方法给出证明.
解:(I)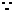 右准线
右准线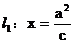 ,渐近线
,渐近线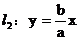
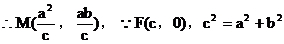 ,
,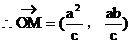
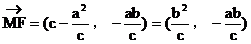
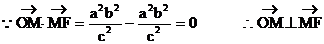 ……3分
……3分
(II)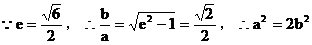
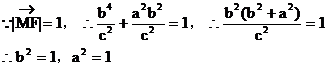
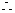 双曲线C的方程为:
双曲线C的方程为: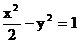 ……7分
……7分
(III)由题意可得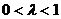 ……8分
……8分
证明:设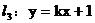 ,点
,点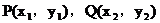
由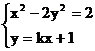 得
得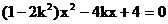
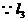 与双曲线C右支交于不同的两点P、Q
与双曲线C右支交于不同的两点P、Q
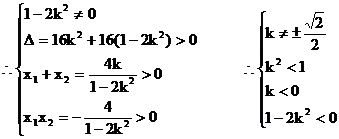
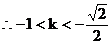 ……11分
……11分
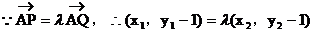 ,得
,得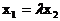
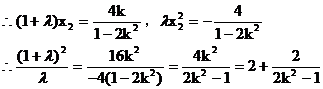
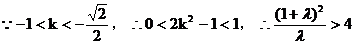

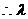 的取值范围是(0,1) ……13分
的取值范围是(0,1) ……13分
22.如图所示,有两条相交成60°角的直路XX′和YY′,交点是O,甲、乙分别在OX、OY上,起初甲离O点3 km,乙离O点1 km,后来两人同时用4 km/h的速度,甲沿XX′方向,乙沿Y′Y的方向步行.
(1)起初,两人的距离是多少?
|
21.已知△ABC的顶点为A(0,0),B(4,8),C(6,-4).M点在线段AB上,且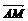 =3
=3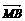 ,P点在线段AC上,△APM的面积是△ABC的面积的一半,求点M、P的坐标.
,P点在线段AC上,△APM的面积是△ABC的面积的一半,求点M、P的坐标.
20.设a=(-1-x)i,b=(1-x)i+yj(x、y∈R,i、j分别是x、y轴正方向上的单位向量),且|a|=|b|.
(1)求点M (x,y)的轨迹C的方程;
(2)过点(4,0)作直线l交曲线C于A、B两点,设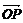 =
=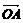 +
+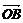 ,求证:四边形OAPB为矩形.
,求证:四边形OAPB为矩形.
19.已知向量a=(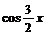 ,
,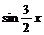 ),b=(
),b=(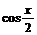 ,
,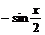 ),且x∈[-
),且x∈[-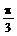 ,
,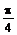 ].
].
(1)求a·b及|a+b|;
(2)若f (x)=a·b-|a+b|,求f (x)的最大值和最小值.
18.设两向量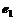 、
、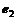 满足|
满足|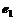 |=2,|
|=2,|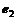 |=1,
|=1,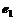 、
、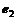 的夹角为60°,若向量2t
的夹角为60°,若向量2t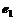 +7
+7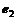 与向量
与向量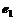 +t
+t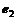 的夹角为钝角,求实数t的取值范围.
的夹角为钝角,求实数t的取值范围.
17.若向量a的始点为A(-2,4),终点为B(2,1).求:
(1)向量a的模.
(2)与a平行的单位向量的坐标.
(3)与a垂直的单位向量的坐标.
16.把函数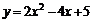 的图象按向量a平移后,得到
的图象按向量a平移后,得到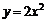 的图象,且a⊥b,c=(1,-1),b·c=4,则b=
.
的图象,且a⊥b,c=(1,-1),b·c=4,则b=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com