
题目列表(包括答案和解析)
3.中学数学中常见应用问题与数学模型
(1)优化问题.实际问题中的“优选”“控制”等问题,常需建立“不等式模型”和“线性规划”问题解决.
(2)预测问题:经济计划、市场预测这类问题通常设计成“数列模型”来解决.
(3)最(极)值问题:工农业生产、建设及实际生活中的极限问题常设计成“函数模型”,转化为求函数的最值.
(4)等量关系问题:建立“方程模型”解决?
(5)测量问题:可设计成“图形模型”利用几何知识解决.
6.(本小题满分14分,第一小问满分2分,第二、第三小问满分各6分)
设数列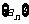 的前
的前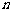 项和为
项和为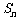 ,已知
,已知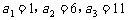 ,且
,且
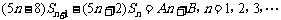 ,
,
其中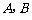 为常数.
为常数.
(Ⅰ)求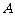 与
与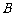 的值;
的值;
(Ⅱ)证明:数列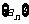 为等差数列;
为等差数列;
(Ⅲ)证明:不等式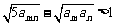 对任何正整数
对任何正整数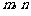 都成立.
都成立.
本小题主要考查等差数列的有关知识、不等式的证明方法,考查思维能力、运算能力.
解:(Ⅰ)由已知,得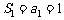 ,
,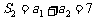 ,
,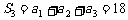 .
.
由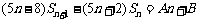 ,知
,知
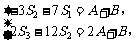 即
即 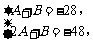
解得 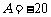 ,
,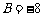 .
.
(Ⅱ)方法1
由(Ⅰ),得 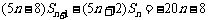 ,
①
,
①
所以
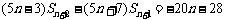 .
②
.
②
②-①,得 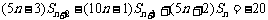 , ③
, ③
所以
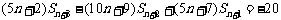 . ④
. ④
④-③,得 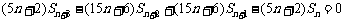 .
.
因为
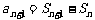 ,
,
所以
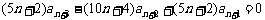 .
.
又因为 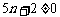 ,
,
所以
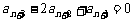 ,
,
即
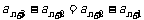 ,
,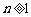 .
.
所以数列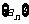 为等差数列.
为等差数列.
方法2
由已知,得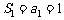 ,
,
又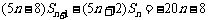 ,且
,且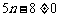 ,
,
所以数列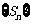 是唯一确定的,因而数列
是唯一确定的,因而数列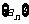 是唯一确定的.
是唯一确定的.
设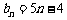 ,则数列
,则数列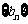 为等差数列,前
为等差数列,前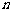 项和
项和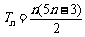 .
.
于是 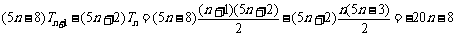 ,
,
由唯一性得 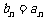 ,即数列
,即数列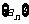 为等差数列.
为等差数列.
(Ⅲ)由(Ⅱ)可知,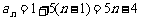 .
.
要证 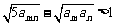 ,
,
只要证 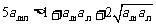 .
.
因为 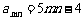 ,
,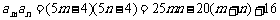 ,
,
故只要证 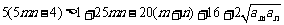 ,
,
即只要证 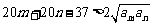 .
.
因为 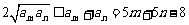
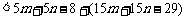
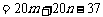 ,
,
所以命题得证.
5.(本小题满分14分,第一小问满分4分,第二小问满分10分)
已知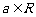 ,函数
,函数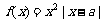 .
.
(Ⅰ)当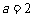 时,求使
时,求使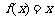 成立的
成立的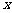 的集合;
的集合;
(Ⅱ)求函数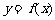 在区间
在区间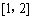 上的最小值.
上的最小值.
本小题主要考查运用导数研究函数性质的方法,考查分类讨论的数学思想和分析推理能力. 满分14分.
解:(Ⅰ)由题意,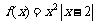 .
.
当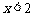 时,
时,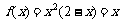 ,解得
,解得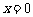 或
或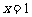 ;
;
当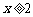 时,
时,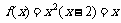 ,解得
,解得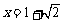 .
.
综上,所求解集为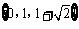 .
.
(Ⅱ)设此最小值为 .
.
①当 时,在区间
时,在区间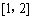 上,
上,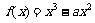 .
.
因为
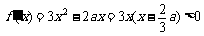 ,
,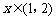 ,
,
则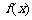 在区间
在区间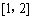 上是增函数,所以
上是增函数,所以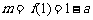 .
.
②当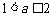 时,在区间
时,在区间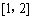 上,
上,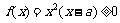 ,由
,由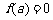 知
知
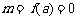 .
.
③当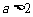 时,在区间
时,在区间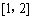 上,
上,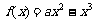 .
.
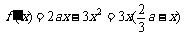 .
.
若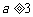 ,在区间
,在区间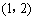 内
内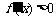 ,从而
,从而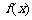 为区间
为区间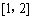 上的增函数,
上的增函数,
由此得
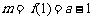 .
.
若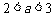 ,则
,则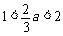 .
.
当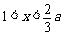 时,
时,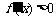 ,从而
,从而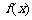 为区间
为区间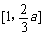 上的增函数;
上的增函数;
当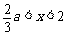 时,
时,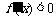 ,从而
,从而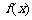 为区间
为区间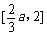 上的减函数.
上的减函数.
因此,当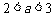 时,
时,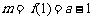 或
或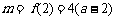 .
.
当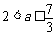 时,
时,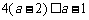 ,故
,故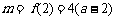 ;
;
当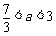 时,
时,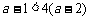 ,故
,故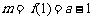 .
.
综上所述,所求函数的最小值

4.(本小题满分14分)
已知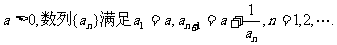
(I)已知数列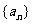 极限存在且大于零,求
极限存在且大于零,求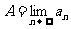 (将A用a表示);
(将A用a表示);
(II)设
(III)若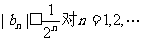 都成立,求a的取值范围.
都成立,求a的取值范围.
本小题主要考查数列、数列极限的概念和数学归纳法,考查灵活运用数学知识分析问题和解决问题的能力,满分14分.
解:(I)由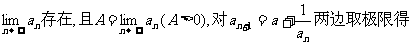
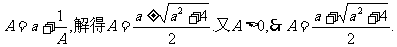
(II)
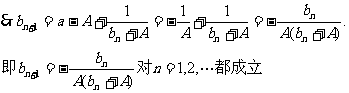
(III)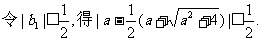

(i)当n=1时结论成立(已验证).
(ii)假设当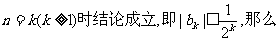

故只须证明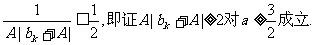
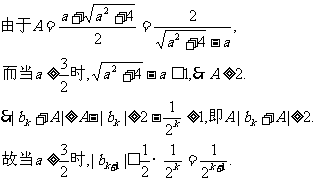
即n=k+1时结论成立.
根据(i)和(ii)可知结论对一切正整数都成立.
故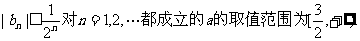
3.(本小题满分12分)
某突发事件,在不采取任何预防措施的情况下发生的概率为0.3,一旦发生,将造成400万元的损失. 现有甲、乙两种相互独立的预防措施可供采用. 单独采用甲、乙预防措施所需的费用分别为45万元和30万元,采用相应预防措施后此突发事件不发生的概率为0.9和0.85. 若预防方案允许甲、乙两种预防措施单独采用、联合采用或不采用,请确定预防方案使总费用最少.
(总费用=采取预防措施的费用+发生突发事件损失的期望值.)
本小题考查概率的基本知识和数学期望概念及应用概率知识解决实际问题的能力,满分12分.
解:①不采取预防措施时,总费用即损失期望为400×0.3=120(万元);
②若单独采取措施甲,则预防措施费用为45万元,发生突发事件的概率为
1-0.9=0.1,损失期望值为400×0.1=40(万元),所以总费用为45+40=85(万元)
③若单独采取预防措施乙,则预防措施费用为30万元,发生突发事件的概率为1-0.85=0.15,损失期望值为400×0.15=60(万元),所以总费用为30+60=90(万元);
④若联合采取甲、乙两种预防措施,则预防措施费用为45+30=75(万元),发生突发事件的概率为(1-0.9)(1-0.85)=0.015,损失期望值为400×0.015=6(万元),所以总费用为75+6=81(万元).
综合①、②、③、④,比较其总费用可知,应选择联合采取甲、乙两种预防措施,可使总费用最少.
2.(本小题满分12分)
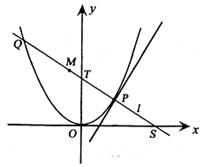 如图,P是抛物线C:y=
如图,P是抛物线C:y=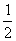 x2上一点,直线l过点P且与抛物线C交于另一点Q.
x2上一点,直线l过点P且与抛物线C交于另一点Q.
(Ⅰ)若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程;
(Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求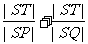 的取值范围.
的取值范围.
本题主要考查直线、抛物线、不等式等基础知识,求轨迹方程的方法,解析几何的基本思想和综合解题能力.满分12分.
解:(Ⅰ)设P(x1,y1),Q(x2,y2),M(x0,y0),依题意x1≠0,y1>0,y2>0.
由y=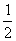 x2,
①
x2,
①
得y'=x.
∴过点P的切线的斜率k切= x1,
∴直线l的斜率kl=-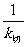 =-
=-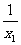 ,
,
∴直线l的方程为y-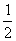 x12=-
x12=-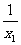 (x-x1),
(x-x1),
方法一:
联立①②消去y,得x2+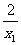 x-x12-2=0.
x-x12-2=0.
∵M是PQ的中点
 x0=
x0=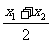 =-
=-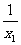 ,
,
∴
y0=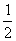 x12-
x12-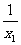 (x0-x1).
(x0-x1).
消去x1,得y0=x02+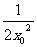 +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+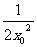 +1(x≠0).
+1(x≠0).
方法二:
由y1=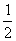 x12,y2=
x12,y2=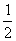 x22,x0=
x22,x0=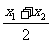 ,
,
得y1-y2=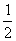 x12-
x12-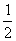 x22=
x22=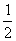 (x1+x2)(x1-x2)=x0(x1-x2),
(x1+x2)(x1-x2)=x0(x1-x2),
则x0=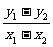 =kl=-
=kl=-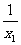 ,
,
∴x1=-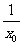 ,
,
将上式代入②并整理,得
y0=x02+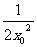 +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+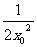 +1(x≠0).
+1(x≠0).
(Ⅱ)设直线l:y=kx+b,依题意k≠0,b≠0,则T(0,b).
分别过P、Q作PP'⊥x轴,QQ'⊥y轴,垂足分别为P'、Q',则
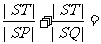
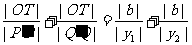 .
.
 y=
y=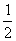 x2
x2
由 消去x,得y2-2(k2+b)y+b2=0. ③
y=kx+b
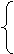 y1+y2=2(k2+b),
y1+y2=2(k2+b),
则
y1y2=b2.
方法一:
∴ |b|(
|b|(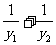 )≥2|b|
)≥2|b|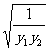 =2|b|
=2|b|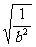 =2.
=2.
∵y1、y2可取一切不相等的正数,
∴ 的取值范围是(2,+
的取值范围是(2,+ ).
).
方法二:
∴ =|b|
=|b|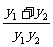 =|b|
=|b|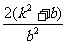 .
.
当b>0时, =b
=b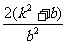 =
=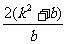 =
=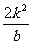 +2>2;
+2>2;
当b<0时, =-b
=-b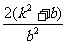 =
=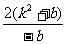 .
.
又由方程③有两个相异实根,得△=4(k2+b)2-4b2=4k2(k2+2b)>0,
于是k2+2b>0,即k2>-2b.
所以 >
>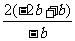 =2.
=2.
∵当b>0时,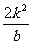 可取一切正数,
可取一切正数,
∴ 的取值范围是(2,+
的取值范围是(2,+ ).
).
方法三:
由P、Q、T三点共线得kTQ=KTP,
即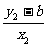 =
=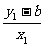 .
.
则x1y2-bx1=x2y1-bx2,即b(x2-x1)=(x2y1-x1y2).
于是b=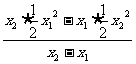 =-
=-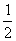 x1x2.
x1x2.
|
|
 =
=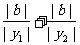 =
=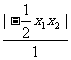 +
+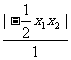 =
=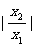 +
+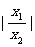 ≥2.
≥2.
∵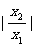 可取一切不等于1的正数,
可取一切不等于1的正数,
∴ 的取值范围是(2,+
的取值范围是(2,+ ).
).
1.(本小题满分14分)
已知f(x)=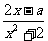 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)=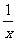 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
本小题主要考查函数的单调性,导数的应用和不等式等有关知识,考查数形结合及分类讨论思想和灵活运用数学知识分析问题和解决问题的能力.满分14分.
解:(Ⅰ)f'(x)=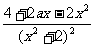 =
=
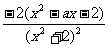 ,
,
∵f(x)在[-1,1]上是增函数,
∴f'(x)≥0对x∈[-1,1]恒成立,
即x2-ax-2≤0对x∈[-1,1]恒成立. ①
设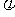 (x)=x2-ax-2,
(x)=x2-ax-2,
方法一:
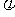 (1)=1-a-2≤0,
(1)=1-a-2≤0,
① 
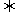 -1≤a≤1,
-1≤a≤1,
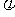 (-1)=1+a-2≤0.
(-1)=1+a-2≤0.
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}. 方法二:
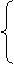
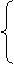
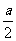 ≥0,
≥0,
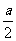 <0,
<0,
① 或
或
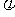 (-1)=1+a-2≤0
(-1)=1+a-2≤0
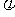 (1)=1-a-2≤0
(1)=1-a-2≤0
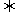 0≤a≤1
或 -1≤a≤0
0≤a≤1
或 -1≤a≤0
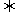 -1≤a≤1.
-1≤a≤1.
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
(Ⅱ)由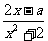 =
=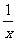 ,得x2-ax-2=0, ∵△=a2+8>0
,得x2-ax-2=0, ∵△=a2+8>0
∴x1,x2是方程x2-ax-2=0的两非零实根,
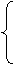 x1+x2=a,
x1+x2=a,
∴
从而|x1-x2|=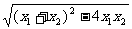 =
=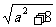 .
.
x1x2=-2,
∵-1≤a≤1,∴|x1-x2|= ≤3.
≤3.
要使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,
当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立,
即m2+tm-2≥0对任意t∈[-1,1]恒成立. ②
设g(t)=m2+tm-2=mt+(m2-2),
方法一:
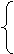 g(-1)=m2-m-2≥0,
g(-1)=m2-m-2≥0,
② 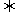
g(1)=m2+m-2≥0,
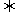 m≥2或m≤-2.
m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
方法二:
当m=0时,②显然不成立;
当m≠0时,
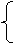
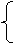 m>0,
m<0,
m>0,
m<0,
②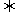 或
或
g(-1)=m2-m-2≥0 g(1)=m2+m-2≥0
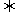 m≥2或m≤-2.
m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
7.(本小题满分12分)
已知数列
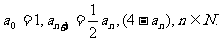
(1)证明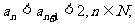
(2)求数列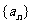 的通项公式an.
的通项公式an.
解:(1)方法一 用数学归纳法证明:
1°当n=1时,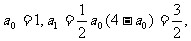
∴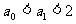 ,命题正确.
,命题正确.
2°假设n=k时有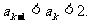
则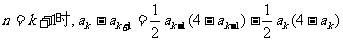
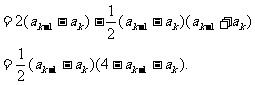
而
又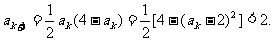
∴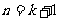 时命题正确.
时命题正确.
由1°、2°知,对一切n∈N时有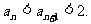
方法二:用数学归纳法证明:
1°当n=1时,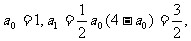 ∴
∴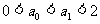 ;
;
2°假设n=k时有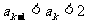 成立,
成立,
令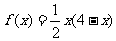 ,
,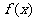 在[0,2]上单调递增,所以由假设
在[0,2]上单调递增,所以由假设
有: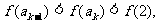 即
即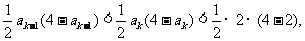
也即当n=k+1时 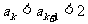 成立,所以对一切
成立,所以对一切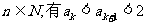
(2)下面来求数列的通项: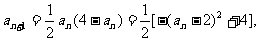 所以
所以
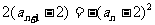
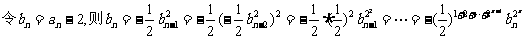 ,
,
又bn=-1,所以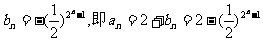
6.(本小题满分12分)
数列{an}满足 .
.
(Ⅰ)用数学归纳法证明: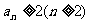 ;
;
(Ⅱ)已知不等式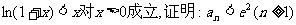 ,其中无理数e=2.71828….
,其中无理数e=2.71828….
(Ⅰ)证明:(1)当n=2时,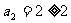 ,不等式成立.
,不等式成立.
(2)假设当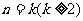 时不等式成立,即
时不等式成立,即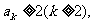
那么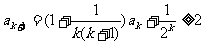 . 这就是说,当
. 这就是说,当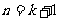 时不等式成立.
时不等式成立.
根据(1)、(2)可知: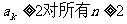 成立.
成立.
(Ⅱ)证法一:
由递推公式及(Ⅰ)的结论有
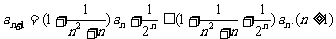
两边取对数并利用已知不等式得

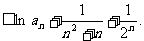 故
故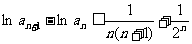
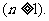
上式从1到 求和可得
求和可得
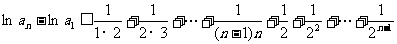

即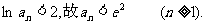
(Ⅱ)证法二:
由数学归纳法易证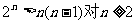 成立,故
成立,故

令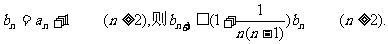
取对数并利用已知不等式得 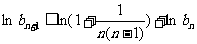
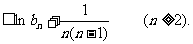
上式从2到n求和得 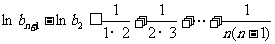
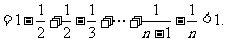
因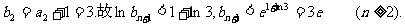
故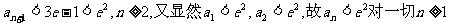 成立.
成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com