
题目列表(包括答案和解析)
11.(全国Ⅰ18)(本小题满分12分)
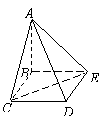
四棱锥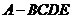 中,底面
中,底面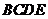 为矩形,侧面
为矩形,侧面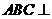 底面
底面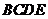 ,
,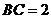 ,
,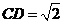 ,
,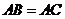 .
.
(Ⅰ)证明: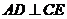 ;
;
 (Ⅱ)设侧面
(Ⅱ)设侧面 为等边三角形,求二面角
为等边三角形,求二面角 的大小.
的大小.
解:(1)取 中点
中点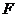 ,连接
,连接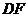 交
交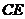 于点
于点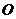 ,
,
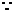
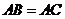 ,
,
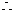
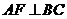 ,
,
又面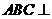 面
面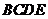 ,
,
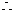
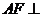 面
面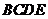 ,
,
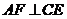 .
.
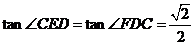 ,
,
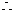
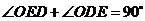 ,
,
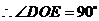 ,即
,即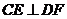 ,
,
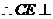 面
面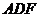 ,
,
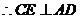 .
.
(2)在面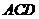 内过
内过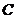 点做
点做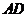 的垂线,垂足为
的垂线,垂足为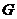 .
.
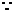
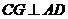 ,
,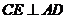 ,
,
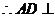 面
面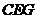 ,
,
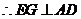 ,
,
则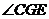 即为所求二面角.
即为所求二面角.
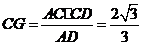 ,
,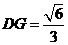 ,
,
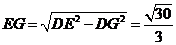 ,
,
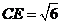 ,
,
则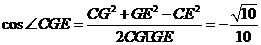 ,
,
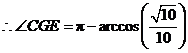 .
.
10.(辽宁19)(本小题满分12分)
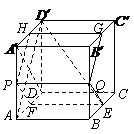 如图,在棱长为1的正方体
如图,在棱长为1的正方体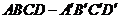 中,AP=BQ=b(0<b<1),截面PQEF∥
中,AP=BQ=b(0<b<1),截面PQEF∥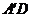 ,截面PQGH∥
,截面PQGH∥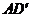 .
.
(Ⅰ)证明:平面PQEF和平面PQGH互相垂直;
(Ⅱ)证明:截面PQEF和截面PQGH面积之和是定值,
并求出这个值;
(Ⅲ)若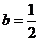 ,求
,求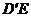 与平面PQEF所成角的正弦值.
与平面PQEF所成角的正弦值.
解法一:
(Ⅰ)证明:在正方体中,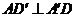 ,
,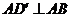 ,
,
又由已知可得
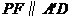 ,
,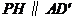 ,
,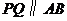 ,
,
所以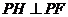 ,
,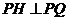 ,
,
所以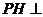 平面
平面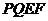 .
.
所以平面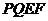 和平面
和平面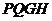 互相垂直.··································································· 4分
互相垂直.··································································· 4分
(Ⅱ)证明:由(Ⅰ)知
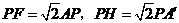 ,又截面PQEF和截面PQGH都是矩形,且PQ=1,所以截面PQEF和截面PQGH面积之和是
,又截面PQEF和截面PQGH都是矩形,且PQ=1,所以截面PQEF和截面PQGH面积之和是
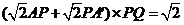 ,是定值.······································································ 8分
,是定值.······································································ 8分
(Ⅲ)解:设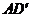 交
交 于点
于点 ,连结
,连结 ,
,
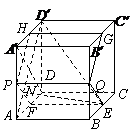 因为
因为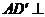 平面
平面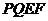 ,
,
所以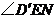 为
为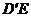 与平面
与平面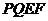 所成的角.
所成的角.
因为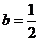 ,所以
,所以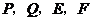 分别为
分别为 ,
,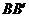 ,
,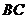 ,
,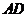 的中点.
的中点.
可知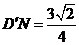 ,
,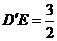 .
.
所以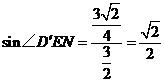 .················································································· 12分
.················································································· 12分
解法二:
以D为原点,射线DA,DC,DD′分别为x,y,z轴的正半轴建立如图的空间直角坐标系D-xyz.由已知得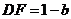 ,故
,故
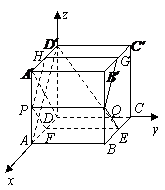
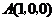 ,
,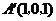 ,
,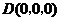 ,
,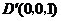 ,
,
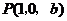 ,
,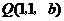 ,
,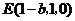 ,
,
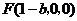 ,
,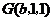 ,
,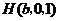 .
.
(Ⅰ)证明:在所建立的坐标系中,可得
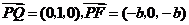 ,
,
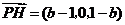 ,
,
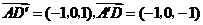 .
.
因为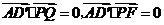 ,所以
,所以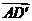 是平面PQEF的法向量.
是平面PQEF的法向量.
因为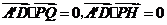 ,所以
,所以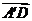 是平面PQGH的法向量.
是平面PQGH的法向量.
因为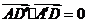 ,所以
,所以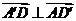 ,
,
所以平面PQEF和平面PQGH互相垂直.········································································· 4分
(Ⅱ)证明:因为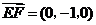 ,所以
,所以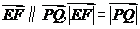 ,又
,又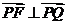 ,所以PQEF为矩形,同理PQGH为矩形.
,所以PQEF为矩形,同理PQGH为矩形.
在所建立的坐标系中可求得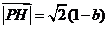 ,
,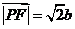 ,
,
所以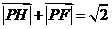 ,又
,又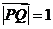 ,
,
所以截面PQEF和截面PQGH面积之和为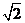 ,是定值.················································· 8分
,是定值.················································· 8分
(Ⅲ)解:由(Ⅰ)知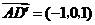 是平面
是平面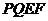 的法向量.
的法向量.
由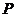 为
为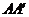 中点可知,
中点可知,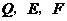 分别为
分别为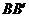 ,
,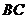 ,
,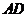 的中点.
的中点.
所以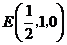 ,
,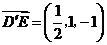 ,因此
,因此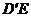 与平面
与平面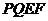 所成角的正弦值等于
所成角的正弦值等于
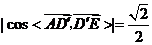 . 12分
. 12分
9.(湖南18)(本小题满分12分)
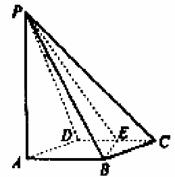 如图所示,四棱锥P-ABCD的底面积ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面积ABCD,PA=
如图所示,四棱锥P-ABCD的底面积ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面积ABCD,PA=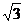 .
.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角A-BE-P的大小.
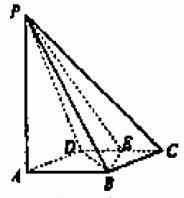 解 解法一(Ⅰ)如图年示,连结BD,由ABCD是菱形且∠BCD=60°知,ΔBCD是等边三角形.因为E是CD的中点,所以BE⊥CD,又AB∥CD,所以BE⊥AB.又因为PA⊥平面ABCD,BE
解 解法一(Ⅰ)如图年示,连结BD,由ABCD是菱形且∠BCD=60°知,ΔBCD是等边三角形.因为E是CD的中点,所以BE⊥CD,又AB∥CD,所以BE⊥AB.又因为PA⊥平面ABCD,BE 平面ABCD,所以PA⊥BE.而PA∩AB=A,因此BE⊥平面PAB.
平面ABCD,所以PA⊥BE.而PA∩AB=A,因此BE⊥平面PAB.
又BE 平面PBE,所以平面PBE⊥平面PAB.
平面PBE,所以平面PBE⊥平面PAB.
(Ⅱ)由(Ⅰ)知,BE⊥平面PAB,PB 平面PAB,所以PB⊥BE.
平面PAB,所以PB⊥BE.
又AB⊥BE,所以∠PBA是二面角A-BE-P的平面角.
在RtΔPAB中,tan∠PBA=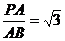 ,∠PBA=60°.
,∠PBA=60°.
故二面角A-BE-P的大小是60°.
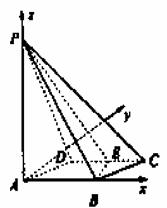 解法二 如图所示,以A为原点,建立空间直角坐标系.则相关各点的坐标分别是A(0,0,0),B(1,0,0),C(
解法二 如图所示,以A为原点,建立空间直角坐标系.则相关各点的坐标分别是A(0,0,0),B(1,0,0),C(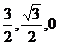 ),D(
),D(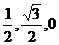 ),P(
),P(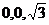 ),E(
),E(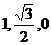 ).
).
(Ⅰ)因为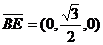 ,平面PAB的一个法向量是
,平面PAB的一个法向量是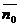 =(0,1,0),所以
=(0,1,0),所以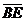 和
和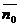 共线.从而BE⊥平面PAB.又因为BE
共线.从而BE⊥平面PAB.又因为BE 平面BEF,所以平面PBE⊥平面PAB.
平面BEF,所以平面PBE⊥平面PAB.
(Ⅱ)易知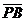 =(1,0,-
=(1,0,-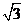 ),
), 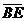 =(0,
=(0,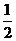
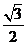 ,0),
,0),
设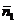 =(x1,y1,z1)是平面PBE的一个法向量,则有
=(x1,y1,z1)是平面PBE的一个法向量,则有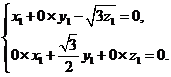
所以y1=0,x1=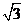 z1.故可取
z1.故可取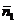 =(
=(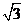 ,0,1).
,0,1).
而平面ABE的一个法向量是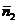 =(0,0,1).
=(0,0,1).
于是,cos<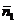 ,
,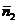 >=
>=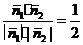 .
.
故二面角A-BE-P的大小是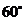
8.(江苏选修)记动点P是棱长为1的正方体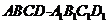 的对角线
的对角线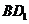 上一点,记
上一点,记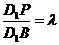 .当
.当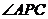 为钝角时,求
为钝角时,求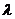 的取值范围.
的取值范围.
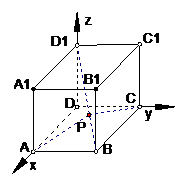 解:由题设可知,以
解:由题设可知,以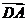 、
、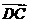 、
、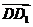 为单位正交基底,建立如图所示的空间直角坐标系
为单位正交基底,建立如图所示的空间直角坐标系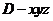 ,则有
,则有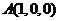 ,
,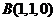 ,
,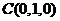 ,
,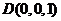
由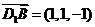 ,得
,得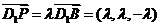 ,所以
,所以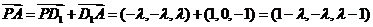
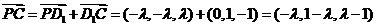
显然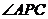 不是平角,所以
不是平角,所以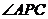 为钝角等价于
为钝角等价于
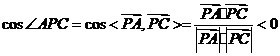 ,则等价于
,则等价于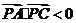
即 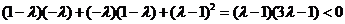 ,得
,得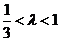
因此,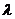 的取值范围是
的取值范围是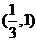
7. (江西20)如图,正三棱锥
(江西20)如图,正三棱锥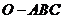 的三条侧棱
的三条侧棱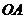 、
、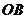 、
、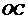 两两垂直,且长度均为2.
两两垂直,且长度均为2.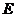 、
、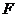 分别是
分别是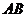 、
、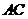 的中点,
的中点,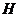 是
是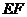 的中点,过
的中点,过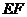 的平面与侧棱
的平面与侧棱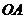 、
、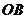 、
、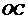 或其延长线分别相交于
或其延长线分别相交于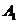 、
、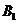 、
、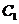 ,已知
,已知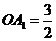 .
.
(1)求证: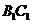 ⊥面
⊥面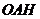 ;
;
(2)求二面角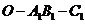 的大小.
的大小.
解
:(1)证明:依题设,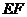 是
是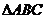 的中位线,所以
的中位线,所以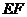 ∥
∥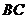 ,
,
则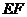 ∥平面
∥平面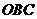 ,所以
,所以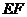 ∥
∥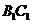 。
。
又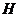 是
是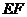 的中点,所以
的中点,所以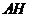 ⊥
⊥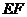 ,
,
则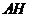 ⊥
⊥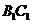 。
。
 因为
因为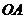 ⊥
⊥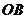 ,
,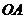 ⊥
⊥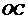 ,
,
所以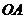 ⊥面
⊥面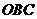 ,则
,则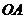 ⊥
⊥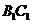 ,
,
因此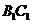 ⊥面
⊥面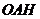 。
。
(2)作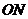 ⊥
⊥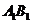 于
于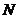 ,连
,连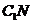 。
。
因为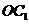 ⊥平面
⊥平面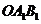 ,
,
根据三垂线定理知,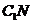 ⊥
⊥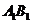 ,
,
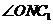 就是二面角
就是二面角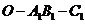 的平面角。
的平面角。
作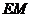 ⊥
⊥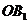 于
于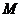 ,则
,则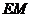 ∥
∥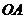 ,则
,则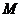 是
是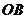 的中点,则
的中点,则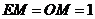 。
。
设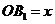 ,由
,由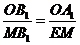 得,
得,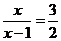 ,解得
,解得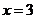 ,
,
在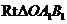 中,
中,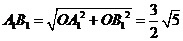 ,则,
,则,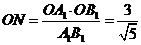 。
。
所以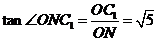 ,故二面角
,故二面角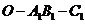 为
为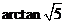 。
。
解法二:(1)以直线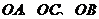 分别为
分别为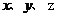 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,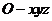 则
则
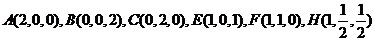
所以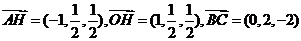
所以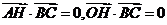
所以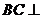 平面
平面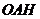
由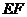 ∥
∥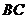 得
得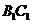 ∥
∥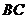 ,故:
,故: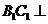 平面
平面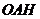
(2)由已知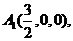 设
设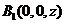
则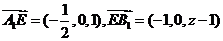
 由
由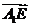 与
与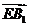 共线得:存在
共线得:存在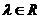 有
有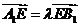 得
得
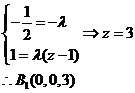
同理: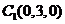
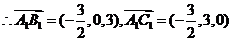
设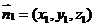 是平面
是平面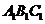 的一个法向量,
的一个法向量,
则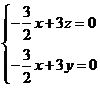 令
令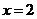 得
得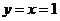
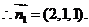
又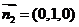 是平面
是平面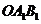 的一个法量
的一个法量
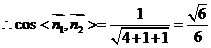
所以二面角的大小为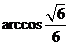
6.(江苏16)(14分)
在四面体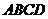 中,
中,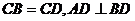 ,且E、F分别是AB、BD的中点,
,且E、F分别是AB、BD的中点,
求证:(1)直线EF//面ACD
(2)面EFC⊥面BCD
[解析]:本小题考查空间直线于平面、平面与平面的位置关系的判定,
考查空间想象能力、推理论证能力。
(1)∵E、F分别是AB、BD的中点 ∴EF是△ABD的中位线∴EF//AD
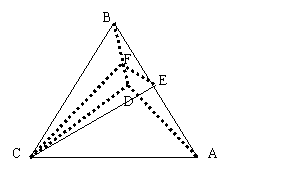 又∵
又∵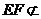 面ACD,AD
面ACD,AD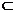 面ACD∴直线EF//面ACD
面ACD∴直线EF//面ACD
 (2)
(2)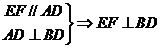
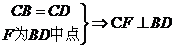
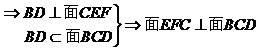
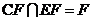
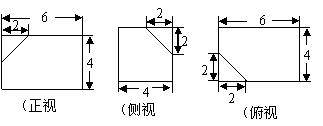
5.(宁夏18)(本小题满分12分)
如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图.它的正视图和俯视图在下面画出(单位:cm)
(Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(Ⅱ)按照给出的尺寸,求该多面体的体积;
(Ⅲ)在所给直观图中连结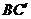 ,证明:
,证明: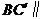 面
面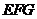 .
.
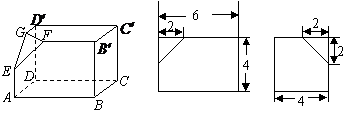

解:(Ⅰ)如图

····················································································· 3分
(Ⅱ)所求多面体体积
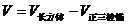
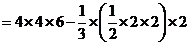
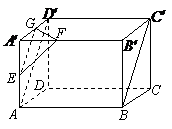
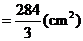 .···································································· 7分
.···································································· 7分
(Ⅲ)证明:在长方体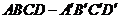 中,
中,
连结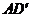 ,则
,则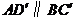 .
.
因为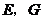 分别为
分别为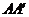 ,
,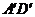 中点,
中点,
所以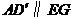 ,
,
从而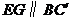 .又
.又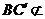 平面
平面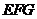 ,
,
所以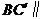 面
面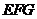 . 12分
. 12分
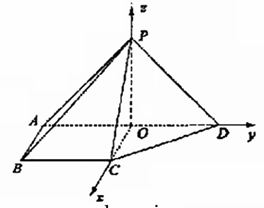
4.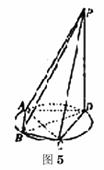 (广东18)(本小题满分14分)
(广东18)(本小题满分14分)
如图5所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP-△BAD.
(1)求线段PD的长;
(2)若PC=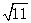 R,求三棱锥P-ABC的体积.
R,求三棱锥P-ABC的体积.
解:(1)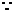 BD是圆的直径
BD是圆的直径
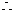
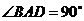 又
又 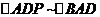 ,
,
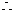
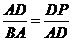 ,
, 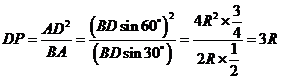 ;
;
(2 ) 在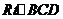 中,
中,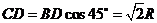
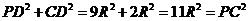
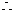
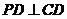 又
又 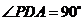
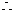
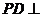 底面ABCD
底面ABCD
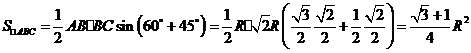
三棱锥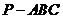 的体积为
的体积为
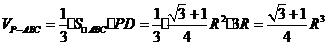 .
.
3. (福建19)(本小题满分12分)
(福建19)(本小题满分12分)
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=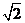 ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点A到平面PCD的距离.
解法一:
(Ⅰ)证明:在△PAD卡中PA=PD,O为AD中点,所以PO⊥AD.
又侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,PO 平面PAD,
平面PAD,
所以PO⊥平面ABCD.
(Ⅱ)连结BO,在直角梯形ABCD中,BC∥AD,AD=2AB=2BC,
有OD∥BC且OD=BC,所以四边形OBCD是平行四边形,
所以OB∥DC.
由(Ⅰ)知PO⊥OB,∠PBO为锐角,
所以∠PBO是异面直线PB与CD所成的角.
因为AD=2AB=2BC=2,在Rt△AOB中,AB=1,AO=1,所以OB=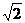 ,
,
在Rt△POA中,因为AP=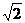 ,AO=1,所以OP=1,
,AO=1,所以OP=1,
在Rt△PBO中,PB=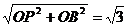 ,
,
cos∠PBO=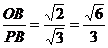 ,
,
所以异面直线PB与CD所成的角的余弦值为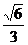 .
.
(Ⅲ)由(Ⅱ)得CD=OB=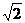 ,
,
在Rt△POC中,PC=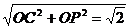 ,
,
 所以PC=CD=DP,S△PCD=
所以PC=CD=DP,S△PCD=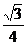 ·2=
·2=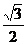 .
.
又S△=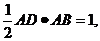
设点A到平面PCD的距离h,
由VP-ACD=VA-PCD,
得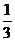 S△ACD·OP=
S△ACD·OP=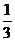 S△PCD·h,
S△PCD·h,
即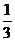 ×1×1=
×1×1=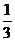 ×
×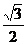 ×h,
×h,
解得h=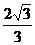 .
.
 解法二:
解法二:
(Ⅰ)同解法一,
(Ⅱ)以O为坐标原点,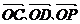 的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系O-xyz.
的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系O-xyz.
则A(0,-1,0),B(1,-1,0),C(1,0,0),
D(0,1,0),P(0,0,1).
所以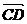 =(-1,1,0),
=(-1,1,0),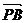 =(t,-1,-1),
=(t,-1,-1),
∞〈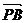 、
、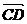 〉=
〉=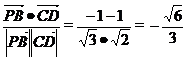 ,
,
所以异面直线PB与CD所成的角的余弦值为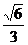 ,
,
(Ⅲ)设平面PCD的法向量为n=(x0,y0,x0),
由(Ⅱ)知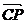 =(-1,0,1),
=(-1,0,1),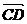 =(-1,1,0),
=(-1,1,0),
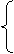
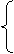 则 n·
则 n·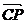 =0,所以 -x0+ x0=0,
=0,所以 -x0+ x0=0,
n·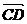 =0, -x0+ y0=0,
即x0=y0=x0,
=0, -x0+ y0=0,
即x0=y0=x0,
取x0=1,得平面的一个法向量为n=(1,1,1).
又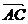 =(1,1,0).
=(1,1,0).
从而点A到平面PCD的距离d=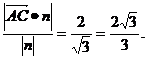
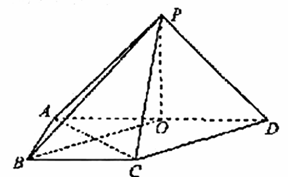
2.(北京16)(本小题共14分)
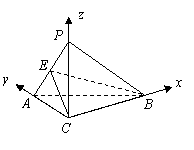
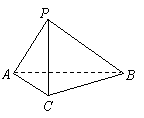 如图,在三棱锥
如图,在三棱锥 中,
中,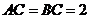 ,
,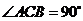 ,
,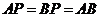 ,
,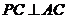 .
.
(Ⅰ)求证: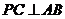 ;
;
(Ⅱ)求二面角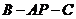 的大小.
的大小.
解法一:
(Ⅰ)取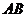 中点
中点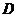 ,连结
,连结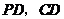 .
.
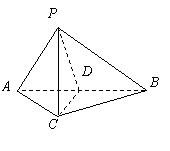
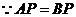 ,
,
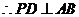 .
.
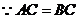 ,
,
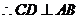 .
.
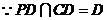 ,
,
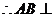 平面
平面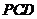 .
.
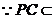 平面
平面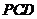 ,
,
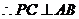 .
.
(Ⅱ)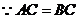 ,
,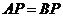 ,
,
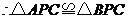 .
.
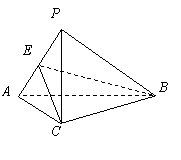 又
又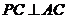 ,
,
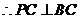 .
.
又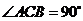 ,即
,即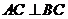 ,且
,且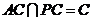 ,
,
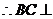 平面
平面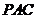 .
.
取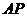 中点
中点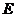 .连结
.连结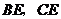 .
.
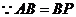 ,
,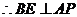 .
.
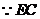 是
是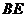 在平面
在平面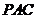 内的射影,
内的射影,
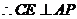 .
.
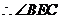 是二面角
是二面角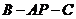 的平面角.
的平面角.
在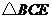 中,
中,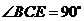 ,
,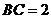 ,
,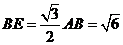 ,
,
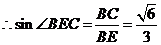 .
.
 二面角
二面角 的大小为
的大小为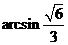 .
.
解法二:
(Ⅰ)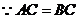 ,
,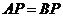 ,
,
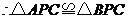 .
.
又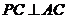 ,
,
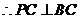 .
.
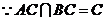 ,
,
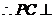 平面
平面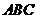 .
.
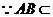 平面
平面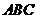 ,
,
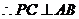 .
.
(Ⅱ)如图,以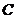 为原点建立空间直角坐标系
为原点建立空间直角坐标系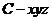 .
.
则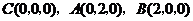 .
.
设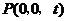 .
.
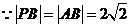 ,
,
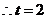 ,
,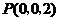 .
.
取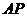 中点
中点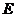 ,连结
,连结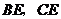 .
.
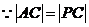 ,
,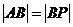 ,
,
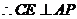 ,
,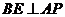 .
.
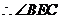 是二面角
是二面角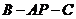 的平面角.
的平面角.
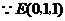 ,
,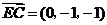 ,
,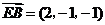 ,
,
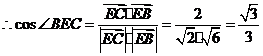 .
.
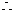 二面角
二面角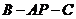 的大小为
的大小为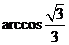 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com