
题目列表(包括答案和解析)
2.若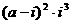 为纯虚数,则实数
为纯虚数,则实数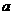 等于 ( )
等于 ( )
A.0 B.1 C.-1 D.2
1.若集合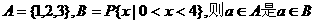 的 ( )
的 ( )
A.充发不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
17 (12分)
 已知
已知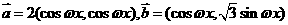
(其中0< <1),函数
<1),函数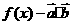 若直线
若直线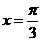 是
是
函数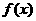 图像的一条对称轴,
图像的一条对称轴,
(I)
试求 的值;
的值;
(II)
先列表在作出函数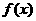 在区间
在区间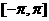 上的图像
上的图像
18 (12分)
某研究机构准备举办一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示
|
版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
|
人数 |
20 |
15 |
5 |
10 |
(I) 从这50名教师中随机选出2名,问这2人使用相同版本教材的概率是多少?
(II) 现从这50名教师中随机选出2名教师做问卷调查,若选出3名教师都使用人教版教材,求恰有1人使用人教版A版的概率是多少?
(III)
若随机选出的2名教师都是用人教版教材,设其中使用人教A版教材的教师人数为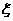 的分布列和数学期望。
的分布列和数学期望。
19 (12分)
如图,已知里棱锥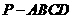 的底面为直角梯形,
的底面为直角梯形,
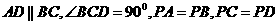
(I)
 证明平面
证明平面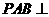 平面ABCD;
平面ABCD;
(II)
如果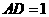
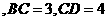 ,且侧面
,且侧面 的面积为8,求四棱锥
的面积为8,求四棱锥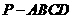 的面积。
的面积。
20 (12分)
已知函数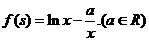
(I)
讨论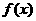 在
在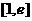 上的单调性;
上的单调性;
(II)
若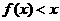 在
在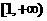 上恒成立,试求
上恒成立,试求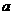 的取值范围。
的取值范围。
21(12分)
已知数列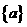 满足
满足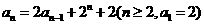 ,
,
(I)
求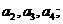
(II)
是否存在一个实数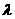 ,使得数列
,使得数列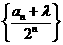 成等差数列,若存在,求出
成等差数列,若存在,求出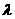 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(III)
求数列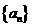 的前n项和,证明:
的前n项和,证明: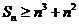
22 (14分)
已知中心在原点、焦点在x轴上的椭圆,其离心率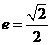 ,且经过抛物线
,且经过抛物线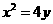 的焦点。
的焦点。
(I) 求椭圆的标准方程;
(II)
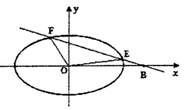 若过点B(2,0)的直线l与椭圆交于不同的亮点E、F(E在B、F之间)且
若过点B(2,0)的直线l与椭圆交于不同的亮点E、F(E在B、F之间)且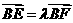 ,试求实数
,试求实数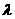 的取值范围。
的取值范围。
淄博市2008-2009学年度高三模拟考试
13 二项式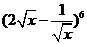 展开式中韩x2项的系数是
。
展开式中韩x2项的系数是
。
14 在如下程序图框中,输入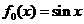 ,则输出的是
,则输出的是
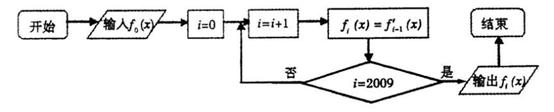
15 已知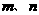 是不同的直线,
是不同的直线,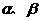 是不重合的平面,给出下列命题:
是不重合的平面,给出下列命题:
①若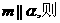 m平行与平面
m平行与平面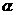 内的无数条直线
内的无数条直线
②若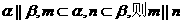
③若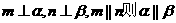
④若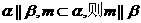
上面命题中,真命题的序号是 (写出所有真命题的序号)
16 在技术工程上,常用到双曲线正弦函数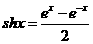 和双曲线余弦函数
和双曲线余弦函数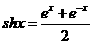 ,而双曲线正弦函数和双曲线余弦函数与我们学过的正弦函数和余弦函数有关类似的性质,比如关于正、余弦函数有
,而双曲线正弦函数和双曲线余弦函数与我们学过的正弦函数和余弦函数有关类似的性质,比如关于正、余弦函数有 成立,而关于双曲正、余弦函数满足
成立,而关于双曲正、余弦函数满足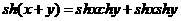 。请你御用类比的思想,写出关于双曲正弦、双曲余弦很熟的一个新关系试
。请你御用类比的思想,写出关于双曲正弦、双曲余弦很熟的一个新关系试
1 已知命题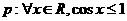 则
则
A 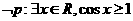 B
B 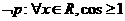
C 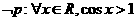 D
D 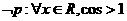
2若复数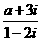 (
(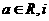 为虚数单位)是纯虚数,则实数
为虚数单位)是纯虚数,则实数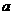 的值为
的值为
A -6 B 6 C -2 D 4
3 下列几何体各自的三视图中,至少有两个试图相同的是

A ①②③ B ①④ C ②④ D①②④
4 5位同学报名参加两个研究性学习小组,每位同学限报其中的一个小组,则不同的报名方法共有
A 10种 B20种 C25种 D32种
5若不等式组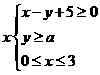 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则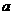 得取值范围是
得取值范围是
A 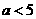 B
B
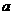
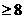 C
C
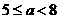 D
D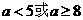
6 过点(0,1)的直线与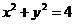 相交于A、B两点,则|AB|的最小值为
相交于A、B两点,则|AB|的最小值为
A 2
B 2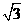 C 3
D2
C 3
D2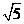
8已7 在三角形ABC中,A=1200,AB=5,BC=7,则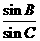 的值为
的值为
A 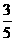 B
B
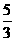 C
C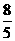 D
D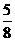
知非零向量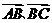 和
和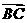 满足
满足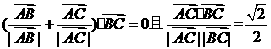 ,则
,则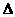 ABC为
ABC为
A 等边三角形 B 等腰非直角三角形 C非等要三角形 D等腰直角三角形
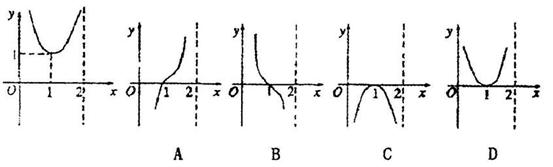
9函数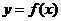 的图像如图所示,则函数
的图像如图所示,则函数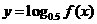 的图像大致是
的图像大致是
10 若点p(2,0)到双曲线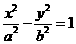 的一条渐近线的距离为
的一条渐近线的距离为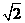 ,则在双曲线德离心率为
,则在双曲线德离心率为
A 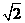 B
B
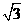 C
C
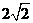 D
D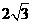
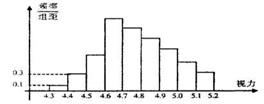 11 为了解某校高三学生的视力情况,随机地抽查了
11 为了解某校高三学生的视力情况,随机地抽查了
该校1000名高三学生的视力情况,得到频率分布直
方图,如图,由于不慎将部分数据丢失,但知道前
4组的频数成等比数列,后6组的频数成等差数列,
设最大频率为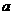 ,视力在4.6到5.0之间的学生数b,则
,视力在4.6到5.0之间的学生数b,则
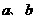 的值分别为
的值分别为
A 2.7,780 B2.7,830 C 0.27,780 D 0.27,830
12 设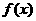 是定义在R上的齐函数,且党
是定义在R上的齐函数,且党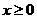 时
时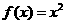 ,若对任意的
,若对任意的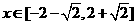 不等式
不等式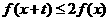 恒成立,则实数t的取值范围是
恒成立,则实数t的取值范围是
A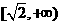 B
B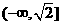
C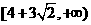 D
D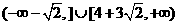
第II卷(非选择题 共90分)
22.(本小题满分14分)
如图,曲线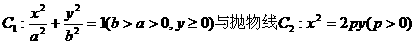 的交点分别为A,B,曲线C1与抛物线C2在点A处的切线分别为
的交点分别为A,B,曲线C1与抛物线C2在点A处的切线分别为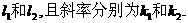
(I) 无关?若是,给出证明;若否,给以说明;
无关?若是,给出证明;若否,给以说明;
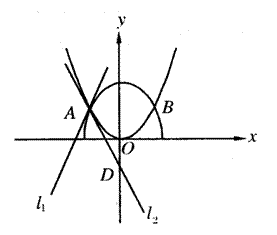 (II)若
(II)若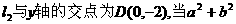 取得最小值9时,求曲线C1与抛物线C2的方程。
取得最小值9时,求曲线C1与抛物线C2的方程。
21.(本小题满分12分)
已知函数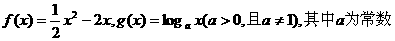 ,如果
,如果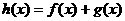 在其定义域上是增函数,且
在其定义域上是增函数,且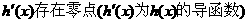 。
。
(I)求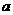 的值;
的值;
(II)设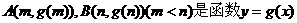 的图象上两点,
的图象上两点,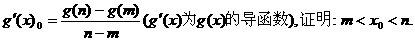
20.(本小题满分12分)
已知数列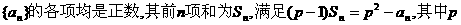 为正常数,且
为正常数,且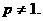
(I)求数列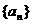 的通项公式;
的通项公式;
(II)设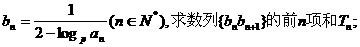
(III)是否存在正整数M,使得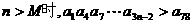 恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。
恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。
19.(本小题满分12分)
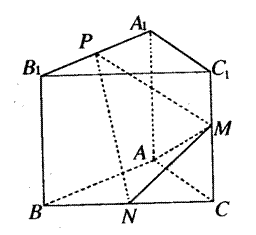
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,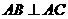 ,M是CC1的中点,N是BC的中点,点P在A1B1上,且满足
,M是CC1的中点,N是BC的中点,点P在A1B1上,且满足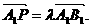
(I)证明: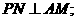
(II)当 取何值时,直线PN与平面ABC所成的角
取何值时,直线PN与平面ABC所成的角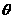 最大?并求该角最大值的正切值;
最大?并求该角最大值的正切值;
(II)若平面PMN与平面ABC所成的二面角为45°,试确定点P的位置。
18.(本小题满分12分)
某车间在两天内,每天生产10件某产品,其中第一天、第二天分别生产了1件、2件次品,而质检部每天要在生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过。
(I)求两天全部通过检查的概率;
(II)若厂内对该车间生产的产品质量采用奖惩制度,两天全不通过检查罚300元,通过1天,2天分别奖300元、900元。那么该车间在这两天内得到奖金的数学期望是多少元?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com