
题目列表(包括答案和解析)
5.解: (1)设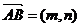 ,则由
,则由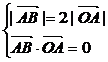 ,可得
,可得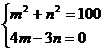 解得
解得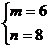 或
或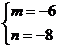 .又
.又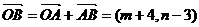 ,且
,且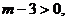 故
故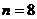 ,
,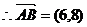
(2由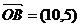 可知直线OB的方程为
可知直线OB的方程为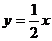
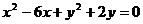 可知圆心为
可知圆心为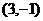 ,半径为
,半径为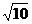 .设圆心关于直线OB的对称点坐标为
.设圆心关于直线OB的对称点坐标为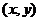 ,由
,由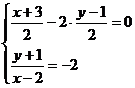
解得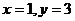 ,故所求圆的方程为
,故所求圆的方程为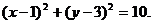
(3)
假设椭圆上存在两点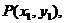
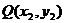 关于直线
关于直线 对称,
对称,
设其中点坐标为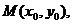 由已知直线
由已知直线 的方程为
的方程为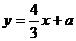 ,可设直线AB的方程为
,可设直线AB的方程为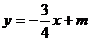
将其与已知椭圆方程联立得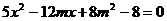 .
.
由韦达定理知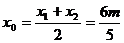 ,
,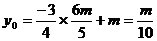 .中点
.中点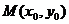 在圆的内部可知
在圆的内部可知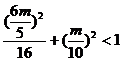 解得
解得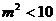 .又
.又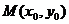 在直线
在直线 上,故
上,故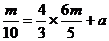 ,解得
,解得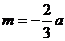 代入
代入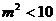 解得
解得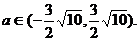 即存在满足题意的实数
即存在满足题意的实数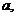 其取值范围为
其取值范围为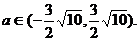
4. 四边形PMNQ为⊙O的内接梯形,圆心O在MN上,向量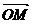 与
与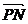 的夹角为150°,
的夹角为150°,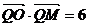
(1)求⊙O的方程
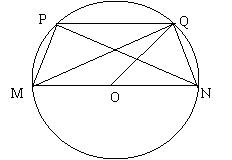 (2)求以M、N为焦点且过P、Q两点的椭圆方程
(2)求以M、N为焦点且过P、Q两点的椭圆方程
(1)以MN所在直线为x轴,MN的中垂线为y轴建立如图所示的直角坐标系
∵ 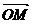 与
与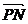 夹角为150°,∴
夹角为150°,∴ 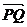 与
与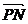 夹角为30°
夹角为30°
∴∠QMN=∠QPN=30°,∴∠OQM=∠OMQ=30°
设⊙O的半径为R,则QM=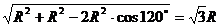
(亦可由Rt△MQN中得)
∵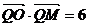 ∴
∴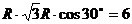 ∴R2=4 ∴⊙O方程为x2+y2=4
∴R2=4 ∴⊙O方程为x2+y2=4
(2)∠QON=60° ∴Q(OQcos60°,OQsin60°) 即Q(1,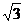 ),∴P(-1,
),∴P(-1,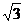 )
)
设所求椭圆方程为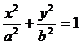 ∵其焦点坐标为(±2,0),点P,Q在椭圆上
∵其焦点坐标为(±2,0),点P,Q在椭圆上
∴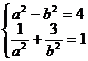 ∴
∴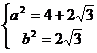 ∴椭圆方程为
∴椭圆方程为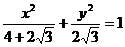
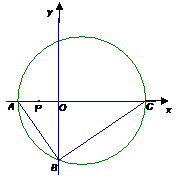
3.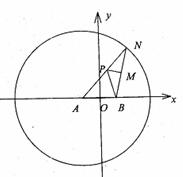 如图,在平面直角坐标系中,N为圆A:
如图,在平面直角坐标系中,N为圆A: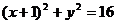 上的一动点,点B(1,0),点M是BN中点,点P在线段AN上,且
上的一动点,点B(1,0),点M是BN中点,点P在线段AN上,且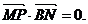
(I)求动点P的轨迹方程;
(II)试判断以PB为直径的圆与圆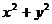 =4的位置关系,并说明理由.
=4的位置关系,并说明理由.
解(I)解:由点M是BN中点,又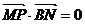 ,
,
可知PM垂直平分BN.所以|PN|=|PB|,又|PA|+|PN|=|AN|,所以|PA|+|PB|=4.
由椭圆定义知,点P的轨迹是以A,B为焦点的椭圆.,设椭圆方程为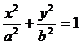 ,由2a=4,2c=2,可得a2=4,b2=3.可知动点P的轨迹方程为
,由2a=4,2c=2,可得a2=4,b2=3.可知动点P的轨迹方程为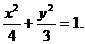
(II)解:设点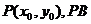 的中点为Q,则
的中点为Q,则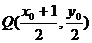 ,
,
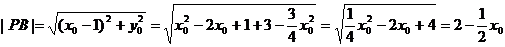 ,
,
即以PB为直径的圆的圆心为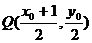 ,半径为
,半径为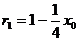 ,
,
又圆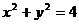 的圆心为O(0,0),半径r2=2,
的圆心为O(0,0),半径r2=2,
又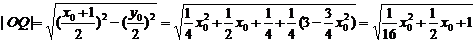
=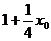 ,故|OQ|=r2-r1,即两圆内切.
,故|OQ|=r2-r1,即两圆内切.
2.已知圆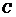 :
: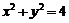 .
.
(1)直线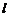 过点
过点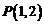 ,且与圆
,且与圆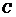 交于
交于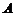 、
、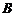 两点,若
两点,若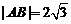 ,求直线
,求直线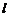 的方程;
的方程;
(2)过圆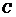 上一动点
上一动点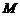 作平行于
作平行于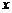 轴的直线
轴的直线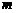 ,设
,设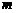 与
与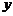 轴的交点为
轴的交点为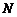 ,若向量
,若向量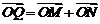 ,求动点
,求动点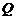 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
解(Ⅰ)①当直线 垂直于
垂直于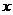 轴时,则此时直线方程为
轴时,则此时直线方程为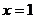 ,
, 与圆的两个交点坐标为
与圆的两个交点坐标为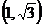 和
和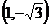
其距离为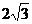 ,满足题意
,满足题意
②若直线 不垂直于
不垂直于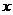 轴,设其方程为
轴,设其方程为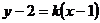 ,即
,即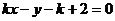 设圆心到此直线的距离为
设圆心到此直线的距离为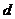 ,则
,则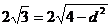 ,得
,得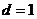 ∴
∴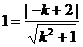 ,
,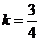 ,故所求直线方程为
,故所求直线方程为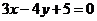 综上所述,所求直线为
综上所述,所求直线为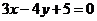 或
或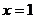
(Ⅱ)设点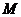 的坐标为
的坐标为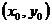 ,
,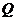 点坐标为
点坐标为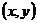 则
则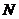 点坐标是
点坐标是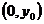
∵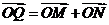 ,∴
,∴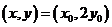 即
即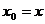 ,
,
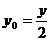
又∵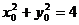 ,∴
,∴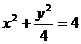 由已知,直线m //ox轴,所以,
由已知,直线m //ox轴,所以,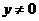
∴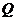 点的轨迹方程是
点的轨迹方程是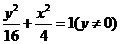 , 轨迹是焦点坐标为
, 轨迹是焦点坐标为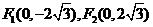 ,长轴为8的椭圆,并去掉
,长轴为8的椭圆,并去掉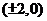 两点。
两点。
1.将圆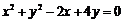 按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使
按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使 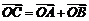 =λa,求直线l的方程及对应的点C的坐标.
=λa,求直线l的方程及对应的点C的坐标.
解:圆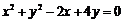 化为标准方程为
化为标准方程为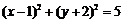 ,按向量a=(-1,2)平移得⊙O方程为 x2+y2=5.∵
,按向量a=(-1,2)平移得⊙O方程为 x2+y2=5.∵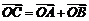 =λa,且|
=λa,且|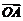 |=|
|=|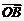 |,∴
|,∴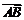 ⊥
⊥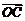 ,
,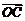 ∥a.
∥a.
∴kAB=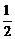 .设直线l的方程为y=
.设直线l的方程为y=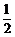 x+m,联立,得
x+m,联立,得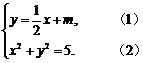
将方程(1)代入(2),整理得5x2+4mx+4m2-20=0.(※)设A(x1,y1),B(x2,y2),则 x1+x2=-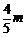 ,y1+y2=
,y1+y2=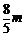 ,
,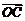 =(-
=(-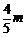 ,
,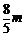 ). 因为点C在圆上,所以
). 因为点C在圆上,所以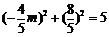 ,解之,得
,解之,得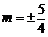 .
.
此时,(※)式中的△=16m2-20(4m2-20)=300>0.所求的直线l的方程为2x-4y+5=0,对应的C点的坐标为(-1,2);或直线l的方程为2x-4y-5=0,对应的C点的坐标为(1,-2).
4.解(Ⅰ)∵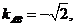
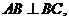 ∴
∴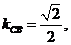 ∴
∴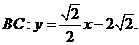 (Ⅱ)在上式中,令
(Ⅱ)在上式中,令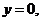 得:
得: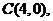 ∴圆心
∴圆心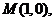 .又∵
.又∵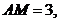 .∴外接圆的方程为
.∴外接圆的方程为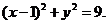
(Ⅲ)∵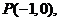
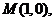 ∵圆
∵圆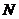 过点
过点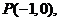 ,∴
,∴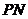 是该圆的半径,又∵动圆
是该圆的半径,又∵动圆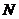 与圆
与圆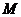 内切,∴
内切,∴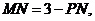 即
即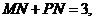 .∴点
.∴点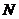 的轨迹是以
的轨迹是以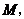
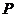 为焦点,长轴长为3的椭圆.
为焦点,长轴长为3的椭圆.
∴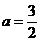 ,
, 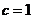 ,
,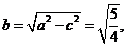 ∴轨迹方程为
∴轨迹方程为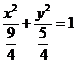 .
.
赣马高级中学解答题专题训练20
解析几何(三) 编写:刘建自 审核:王怀学
3.解:(Ⅰ)依题意,有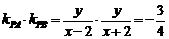 (
(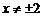 ),化简得
),化简得
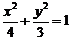 (
(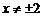 ),
),
这就是动点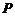 的轨迹
的轨迹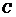 的方程;
的方程;
(Ⅱ)依题意,可设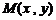 、
、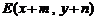 、
、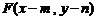 ,则有
,则有
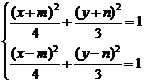 ,两式相减,得
,两式相减,得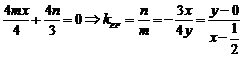 ,由此得点
,由此得点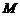 的轨迹方程为
的轨迹方程为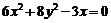 (
(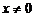 ). 设直线
). 设直线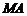 :
: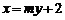 (其中
(其中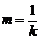 ),则
),则
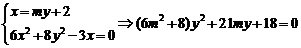 ,
,
故由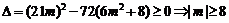 ,即
,即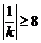 ,解之得
,解之得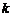 的取值范围是
的取值范围是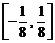 .
.
2.已知直线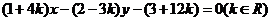 所经过的定点
所经过的定点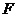 恰好是椭圆
恰好是椭圆 的一个焦点,且椭圆
的一个焦点,且椭圆 上的点到点
上的点到点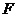 的最大距离为8.
的最大距离为8.
(Ⅰ)求椭圆 的标准方程;(7分)
的标准方程;(7分)
(Ⅱ)已知圆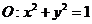 ,直线
,直线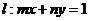 .试证明当点
.试证明当点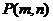 在椭圆
在椭圆 上运动时,直线
上运动时,直线 与圆
与圆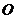 恒相交;并求直线
恒相交;并求直线 被圆
被圆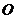 所截得的弦长的取值范围. (8分)
所截得的弦长的取值范围. (8分)
解: (Ⅰ)由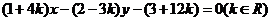 ,得
,得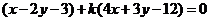 ,
,
则由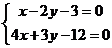 ,解得F(3,0). 设椭圆
,解得F(3,0). 设椭圆 的方程为
的方程为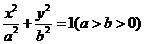 ,则
,则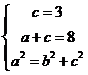 ,解得
,解得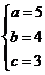 所以椭圆
所以椭圆 的方程为
的方程为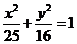
(Ⅱ)因为点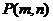 在椭圆
在椭圆 上运动,所以
上运动,所以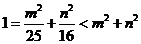 , 从而圆心
, 从而圆心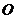 到直线
到直线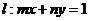 的距离
的距离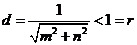 .
所以直线
.
所以直线 与圆
与圆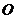 恒相交
恒相交
又直线 被圆
被圆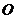 截得的弦长为
截得的弦长为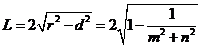
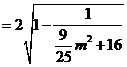
由于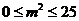 ,所以
,所以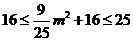 ,则
,则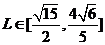 ,
,
即直线 被圆
被圆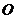 截得的弦长的取值范围是
截得的弦长的取值范围是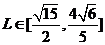
1.已知:以点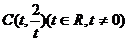 为圆心的圆与
为圆心的圆与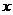 轴交于点
轴交于点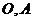 ,与
,与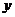 轴交于点
轴交于点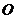 、
、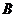 ,其中
,其中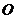 为原点。求证:
为原点。求证: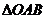 的面积为定值;
的面积为定值;
(2) 设直线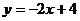 与圆
与圆 交于点
交于点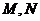 ,若
,若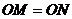 ,求圆
,求圆 的方程。
的方程。
解:(1)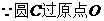 ,
,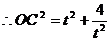 。设圆
。设圆 的方程是
的方程是 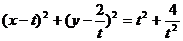
令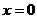 ,得
,得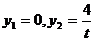 ;令
;令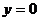 ,得
,得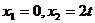
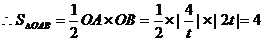 ,即:
,即: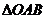 的面积为定值。
的面积为定值。
(2)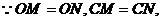
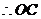 垂直平分线段
垂直平分线段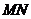 。
。 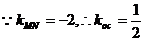 ,
,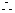 直线
直线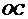 的方程是
的方程是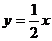
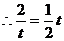 ,解得:
,解得: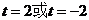 当
当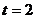 时,圆心
时,圆心 的坐标为
的坐标为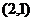 ,
,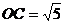 , 此时
, 此时 到直线
到直线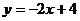 的距离
的距离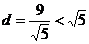 ,圆
,圆 与直线
与直线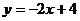 相交于两点。当
相交于两点。当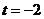 时,圆心
时,圆心 的坐标为
的坐标为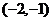 ,
,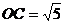 ,此时
,此时 到直线
到直线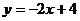 的距离
的距离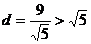 ,圆
,圆 与直线
与直线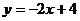 不相交,
不相交,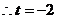 不符合题意舍去。
不符合题意舍去。 圆
圆 的方程为
的方程为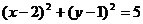
5.已知平面区域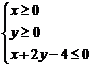 恰好被面积最小的圆
恰好被面积最小的圆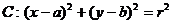 及其内
及其内
部所覆盖.
(Ⅰ)试求圆 的方程.
的方程.
(Ⅱ)若斜率为1的直线 与圆C交于不同两点
与圆C交于不同两点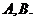 满足
满足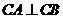 ,求直线
,求直线 的方程.
的方程.
解:(1)由题意知此平面区域表示的是以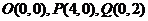 构成的三角形及其内部,且△
构成的三角形及其内部,且△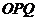 是直角三角形,所以覆盖它的且面积最小的圆是其外接圆,故圆心是(2,1),半径是
是直角三角形,所以覆盖它的且面积最小的圆是其外接圆,故圆心是(2,1),半径是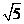 ,所以圆
,所以圆 的方程是
的方程是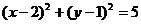 .
.
(2)设直线 的方程是:
的方程是: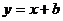 .
.
因为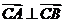 ,所以圆心
,所以圆心 到直线
到直线 的距离是
的距离是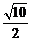 , 即
, 即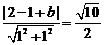
解得: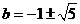 .所以直线
.所以直线 的方程是:
的方程是: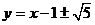 .
.
赣马高级中学解答题专题训练19答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com