
题目列表(包括答案和解析)
1.集合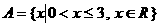 ,
,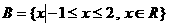 ,则
,则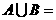 _____________.
_____________.
23.函数是这样定义的:对于任意整数 ,当实数
,当实数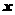 满足不等式
满足不等式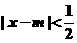 时,有
时,有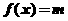 .
.
(1)求函数的定义域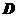 ,并画出它在
,并画出它在 上的图像;
上的图像;
(2)若数列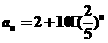 ,记
,记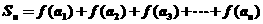 ,求
,求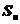 ;
;
(3)若等比数列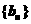 的首项是
的首项是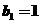 ,公比为
,公比为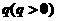 ,又
,又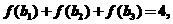 求公比
求公比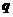 的取值范围.
的取值范围.
(1)函数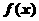 的定义域是
的定义域是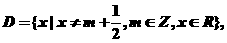
图像如图所示,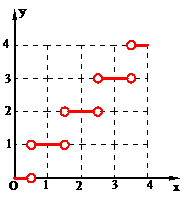
(2)由于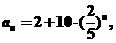 所以
所以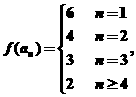
因此,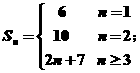
(3)由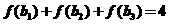 得
得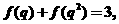
当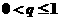 时,则
时,则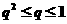 ,所以
,所以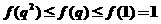 ,
,
则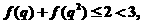 不合题意;
不合题意;
当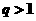 时,则
时,则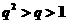 ,所以
,所以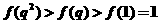
只可能是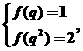 即
即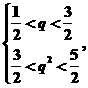 解之得
解之得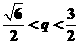 .
.
22.已知向量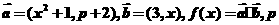 是实数.
是实数.
(1)若存在唯一实数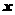 ,使
,使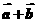 与
与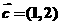 平行,试求
平行,试求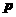 的值;
的值;
(2)若函数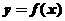 是偶函数,试求函数
是偶函数,试求函数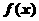 在区间
在区间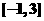 上的值域;
上的值域;
(3)已知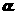 :函数
:函数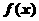 在区间
在区间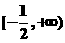 上是增函数,
上是增函数,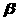 :方程
:方程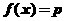 有小于
有小于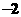 的实根.试问:
的实根.试问: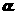 是
是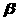 的什么条件(指出充分性和必要性)?请说明理由.
的什么条件(指出充分性和必要性)?请说明理由.
(1)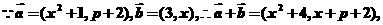
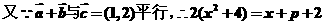 ,即
,即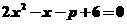 ,
,
依题意可知,方程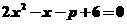 有两个相等的实根,∴△=
有两个相等的实根,∴△=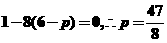
(2)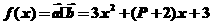 是偶函数,
是偶函数,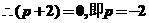
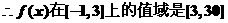
(3)由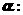 函数
函数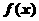 在区间
在区间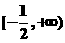 上是增函数,知
上是增函数,知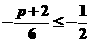 ,
,
 由
由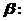 方程
方程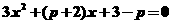 有小于-2的实根,
有小于-2的实根,
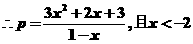
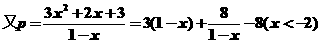 的值域为
的值域为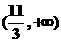
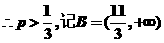
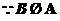 ,所以
,所以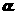 是
是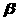 的必要不充分条件.
的必要不充分条件.
21.已知 为实数,
为实数,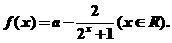
(1)求证:对于任意实数 ,
,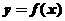 在
在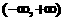 上是增函数;
上是增函数;
(2)当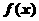 是奇函数时,若方程
是奇函数时,若方程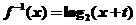 总有实数根,求实数
总有实数根,求实数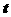 的取值范围.
的取值范围.
因为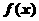 是R上的奇函数,所以
是R上的奇函数,所以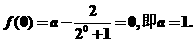
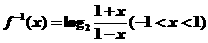
由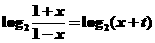 得
得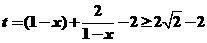
当且仅当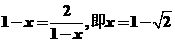 时等号成立, 所以,
时等号成立, 所以,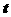 的取值范围是
的取值范围是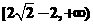
20.已知角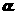 的顶点在原点,始边与
的顶点在原点,始边与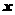 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点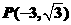 .
.
(1)求行列式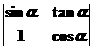 的值;
的值;
(2)若函数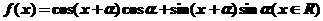 ,
,
求函数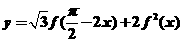 的最大值,并指出取到最大值时
的最大值,并指出取到最大值时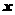 的值.
的值.
(1)因为角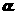 终边经过点
终边经过点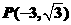 ,所以
,所以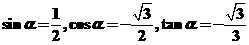
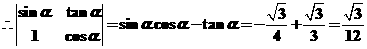 ;
;
(2)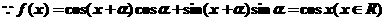
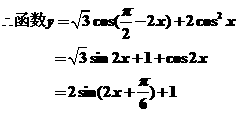
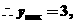 此时
此时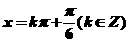
19.如图,直四棱柱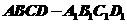 中,底面
中,底面 是直角梯形,
是直角梯形,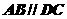 ,
,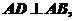
且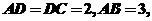 1)求异面直线
1)求异面直线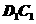 与
与 所成角的大小.2)求AD1和平面BB1D1D所成角的大小
所成角的大小.2)求AD1和平面BB1D1D所成角的大小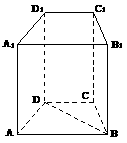
18.一质点 从原点
从原点 出发沿向量
出发沿向量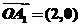 到达点
到达点 ,再沿
,再沿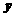 轴正方向从点
轴正方向从点 前进
前进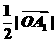 到达点
到达点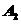 ,再沿
,再沿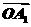 的方向从点
的方向从点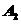 前进
前进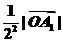 到达点
到达点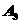 ,再沿
,再沿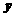 轴正方向从点
轴正方向从点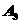 前进
前进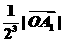 到达点
到达点 ,┅,这样无限前进下去,则质点
,┅,这样无限前进下去,则质点 最终到达的点坐标是( D )
最终到达的点坐标是( D )
A.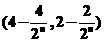 B.
B.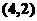 C.
C.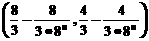 D.
D.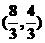
17.已知图1中的图像对应的函数为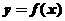 ,则图2中的图像对应的函数在下列给出的四式中,只可能是
( C )
,则图2中的图像对应的函数在下列给出的四式中,只可能是
( C )
A. B.
B.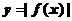 C.
C.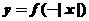 D.
D.
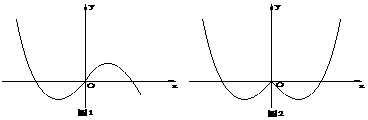
16.复数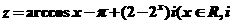 是虚数单位),在复平面内的对应点只可能位于( B )
是虚数单位),在复平面内的对应点只可能位于( B )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
15.给定空间中的直线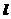 及平面
及平面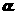 ,条件“直线
,条件“直线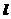 与平面
与平面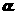 内无数条直线都垂直”是“直线
内无数条直线都垂直”是“直线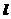 与平面
与平面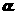 垂直”的
( B )
垂直”的
( B )
A.充分非必要条件 B.必要非充分条件 C. 充要条件 D. 既非充分也非必要条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com