
题目列表(包括答案和解析)
20.(本小题满分14分)在平面直角坐标系 中 ,已知以
中 ,已知以 为圆心的圆与直线
为圆心的圆与直线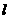 :
: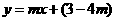 ,
,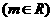 恒有公共点,且要求使圆
恒有公共点,且要求使圆 的面积最小。
的面积最小。
(1)写出圆 的方程;
的方程;
(2)圆 与
与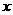 轴相交于A、B两点,圆内的动点P使
轴相交于A、B两点,圆内的动点P使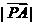 、
、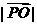 、
、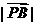 成等比数列,求
成等比数列,求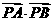 的范围;
的范围;
(3) 已知定点Q(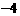 ,3),直线
,3),直线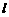 与圆
与圆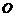 交于M、N两点,试判断
交于M、N两点,试判断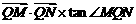 是否有最大值,若存在求出最大值,并求出此时直线
是否有最大值,若存在求出最大值,并求出此时直线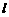 的方程,若不存在,给出理由。
的方程,若不存在,给出理由。
19. (本小题满分14分)
(本小题满分14分)
(1)证明:
连接B1C,与BC1相交于O,连接OD
∵BCC1B1是矩形,
∴O是B1C的中点.
又D是AC的中点,
∴OD//AB1.
∵AB1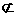 面BDC1,OD
面BDC1,OD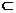 面BDC1,
面BDC1,
∴AB1//面 …………
4分
…………
4分
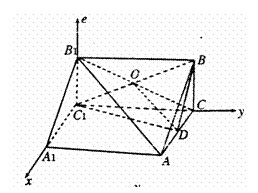 (2)解:如图,以C1为原点,以C1A1为X轴,以CC1为Y轴,以C1B1为Z轴建立空间直角坐标系,则 C1(0,0,0),B(0,3,2),C(0,3,0),A(2,3,0), D(1,3,0)
(2)解:如图,以C1为原点,以C1A1为X轴,以CC1为Y轴,以C1B1为Z轴建立空间直角坐标系,则 C1(0,0,0),B(0,3,2),C(0,3,0),A(2,3,0), D(1,3,0)
设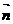 =(x1,y1,z1)是面BDC1的一个法向量,则
=(x1,y1,z1)是面BDC1的一个法向量,则
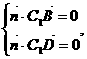 即
即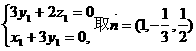 .……………
7分
.……………
7分
易知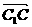 =(0,3,0)是面ABC的一个法向量.
=(0,3,0)是面ABC的一个法向量.
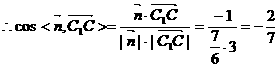
∴二面角C1-BD-C的余弦值为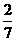 ……………………
9分
……………………
9分
(3)假设侧棱AA1上存在一点P(2,y,0)(0≤y≤3),使得CP⊥面BDC1.
则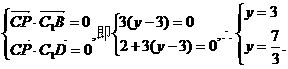 ………………
12分
………………
12分
∴方程组无解.
∴假设不成立.
∴侧棱AA1上不存在点P,使CP⊥面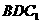 ……………………
14分
……………………
14分
19. (本小题满分14分)如图,三棱柱ABC-A1B1C1
中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.
(本小题满分14分)如图,三棱柱ABC-A1B1C1
中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.
(1)求证:AB1//面BDC1;
(2)求二面角C1-BD-C的余弦值;
(3)在侧棱AA1上是否存在点P,使得
CP⊥面BDC1?并证明你的结论.
18.(本小题满分14分)
(1)由题设,可得=- 3分 则-sinBcosC=2cosBsinA+cosBsinC.
sinBcosC+cosBsinC+2cosBsinA=0, sin(B+C)+2cosB sinA=0, 7分
sinA+2cosB sinA=0. 因为sinA≠0 ,所以cosB=- ,所以B=120o.10分
(2)∵b2=a2+c2-2accosB,∴19=(a+c)2-2ac-2accos120o,∴ac=6. 12分
又a+c=5,可解得或 14分
18.在△ABC中,a、b、c分别是角A、B、C的对边,
且满足 =- .
(1)求角B的大小;
(2)若b=,a+c=5,求a和c的值.
17.存在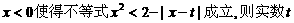 的取值范围是
的取值范围是 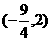
16.已知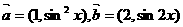 ,其中
,其中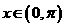 ,若
,若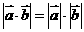 ,则
,则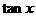 的值等于 ___________ .1
的值等于 ___________ .1
15. 用数字0,1,2,3,4,5,6组成没有重复数字的四位数,其中个位、十位和百位上的数字之和为偶数的四位数共有 324 个(用数字作答)
14.已知△ABC中,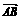 ·
·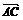 <0,S△ABC=
<0,S△ABC=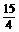 ,|
,|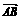 |=3,|
|=3,|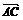 |=5,则∠BAC=
|=5,则∠BAC= 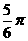
13. 与双曲线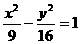 有相同的渐近线,且经过点A(-3,
有相同的渐近线,且经过点A(-3,  )的双曲线方程是
)的双曲线方程是
__ 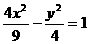
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com