
题目列表(包括答案和解析)
3. 已知命题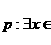 R,
R,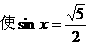
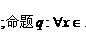 R,
R,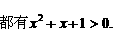 给出下列结论:
给出下列结论:
①命题“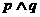 ”是真命题 ②命题“
”是真命题 ②命题“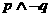 ”是假命题
”是假命题
③命题“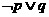 ”是真命题 ④命题“
”是真命题 ④命题“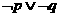 ”是假命题
”是假命题
其中正确的是( )
A.②④ B.②③ C.③④ D.①②③
2. 下列函数中,在区间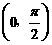 上为增函数且以
上为增函数且以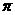 为周期的函数是( )
为周期的函数是( )
A.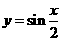 B.
B. 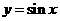 C.
C.  D.
D. 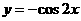
1.复数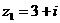 ,
,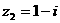 ,则复数
,则复数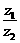 在复平面内对应的点位于( )
在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
21.解:(1)f(x)=x3-x-1,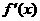 =3x2-1=0,x=
=3x2-1=0,x=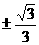 ,
,
x∈(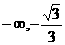 )或x∈(
)或x∈(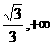 )时
)时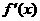 >0,
>0,
x∈(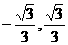 )时
)时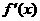 <0,所以函数f(x)的单调递增区间为
<0,所以函数f(x)的单调递增区间为
(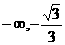 )和(
)和(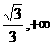 ),函数f(x)的单调递减区间为(
),函数f(x)的单调递减区间为(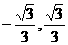 )…5分
)…5分
(2)假设存在这样的a,b,使得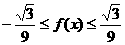 对任意的x∈[0,1]成立,则
对任意的x∈[0,1]成立,则
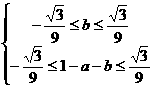 ①,两式相加可得0<
①,两式相加可得0<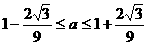 <3,
<3,
所以函数f(x)在区间[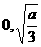 ]递减,在区间[
]递减,在区间[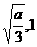 ]递增,
]递增,
所以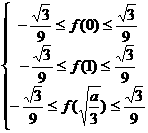 ②,
②,
由不等式组中的第二式加第三式可得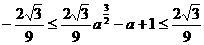 ,
,
由不等式组中的第一式加第三式可得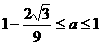 。 …………10分
。 …………10分
记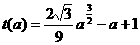 ,
,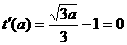 ,a=3,
,a=3,
又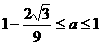 ,
,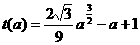 在
在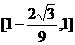 为减函数,
为减函数,
又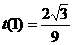 ,所以
,所以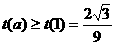 ,所以
,所以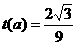 ,
,
所以a=1,代入②式可得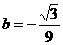 ,所以存在a=1,
,所以存在a=1,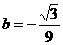 ,
,
使得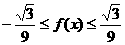 对任意的x∈[0,1]成立。
…………16分
对任意的x∈[0,1]成立。
…………16分
21.(本题满分16分)
已知函数f(x)=x3-ax-b (a,b∈R)
(1)当a=b=1时,求函数f(x)的单调区间
(2)是否存在a,b,使得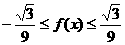 对任意的x∈[0,1]成立?若存在,求出a,b的值,若不存在,说明理由。
对任意的x∈[0,1]成立?若存在,求出a,b的值,若不存在,说明理由。
20.解:(1) …………………………6分
…………………………6分
(2)因为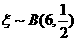
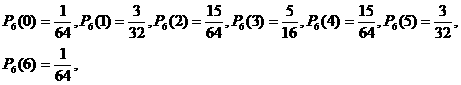
|
ξ |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
|
P |
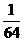 |
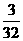 |
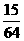 |
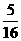 |
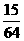 |
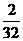 |
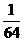 |
………………………………………………11分
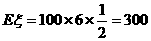 (元)………………………………………………14分
(元)………………………………………………14分
19.证(Ⅰ)因为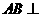 侧面
侧面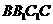 ,故
,故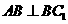
在△BC1C中,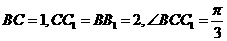
由余弦定理有 [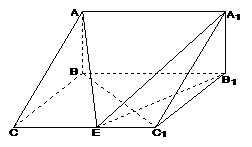
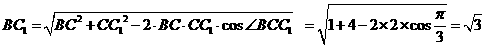
故有 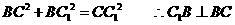
而 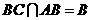 且
且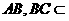 平面
平面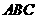

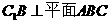 ……4分
……4分
(Ⅱ)由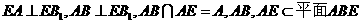
从而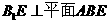 且
且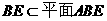 故
故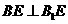
不妨设 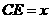 ,则
,则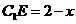 ,则
,则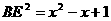
又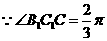 则
则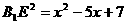
 在直角三角形BEB1中有
在直角三角形BEB1中有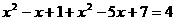
从而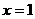 [
[
故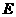 为
为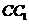 的中点时,
的中点时,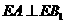 ……9分
……9分
法二:以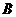 为原点
为原点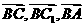 为
为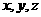 轴,
轴,
设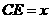 ,则
,则
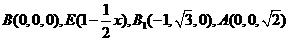
由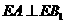 得
得 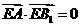 即
即
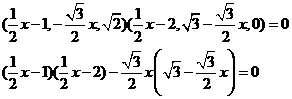
化简整理得 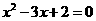
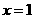 或
或 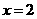
当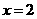 时
时 与
与 重合不满足题意
重合不满足题意
 当
当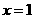 时
时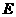 为
为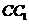 的中点
的中点
故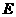 为
为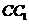 的中点使
的中点使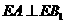 ……9分
……9分
(Ⅲ)取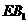 的中点
的中点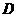 ,
,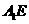 的中点
的中点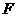 ,
,
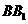 的中点
的中点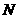 ,
,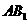 的中点
的中点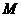
连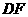 则
则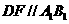 ,连
,连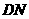 则
则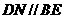 ,
,
连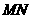 则
则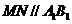
连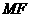 则
则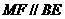 ,且
,且 为矩形,
为矩形,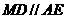
又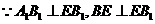 故
故 为所求二面角的平面角
为所求二面角的平面角
在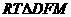 中,
中,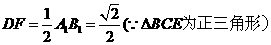
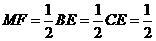
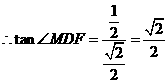 ……14分
……14分
法二:由已知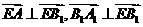 ,
,
所以二面角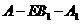 的平面角
的平面角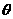 的大小为向量
的大小为向量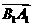 与
与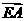 的夹角
的夹角
因为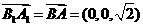
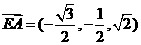
故 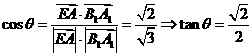 ……14分
……14分
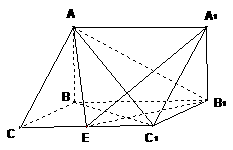
19.(本题满分14分)
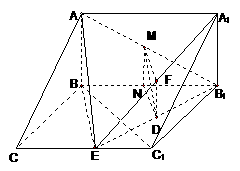
如图,在三棱拄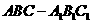 中,
中,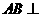 侧面
侧面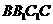 ,已知AA1=2,
,已知AA1=2,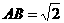 ,
,
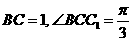
(Ⅰ)求证: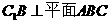 ;
;
(Ⅱ)试在棱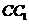 (不包含端点
(不包含端点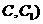 上确定一点
上确定一点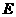 的位置,使得
的位置,使得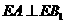 ;
;
(III)在(Ⅱ)的条件下,求二面角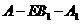 的平面角的正切值.
的平面角的正切值.
18、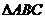 中,三个内角A、B、C所对的边分别为
中,三个内角A、B、C所对的边分别为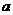 、
、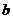 、
、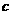 ,若
,若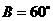 ,
, 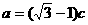 .
.
(1)求角 的大小;
的大小;
(2)已知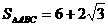 ,求函数
,求函数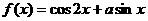 的最大值
的最大值
18.(1)因为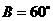 ,所以
,所以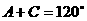 ,
, 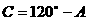 ………………1分
………………1分
因为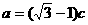 ,由正弦定理可得:
,由正弦定理可得:
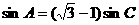 ………………3分
………………3分
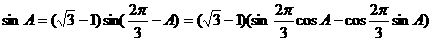
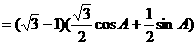 ,整理可得:
,整理可得: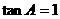 ………………6分
………………6分
所以,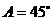 (或
(或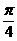 )
………………8分
)
………………8分
(2)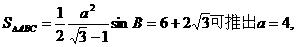
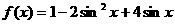 =
=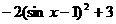 ……11分
……11分
当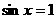 时,函数
时,函数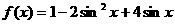 取得最大值3
……14分
取得最大值3
……14分
17、若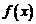 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当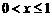 时,
时,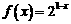 ;当
;当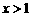 时,
时,
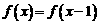 .则函数
.则函数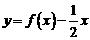 的零点有 7 个。
的零点有 7 个。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com