
题目列表(包括答案和解析)
10、我们将具有下列性质的所有函数组成集合M:函数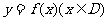 ,对任意
,对任意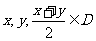 均满足
均满足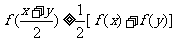 ,当且仅当
,当且仅当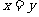 时等号成立。
时等号成立。
(1)若定义在(0,+∞)上的函数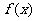 ∈M,试比较
∈M,试比较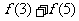 与
与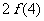 大小.
大小.
(2)设函数g(x)=-x2,求证:g(x)∈M.
[解析] (1)对于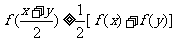 ,令
,令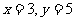 得
得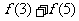 <
<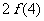
(2)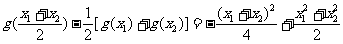
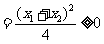
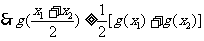 ,所以g(x)∈M
,所以g(x)∈M
9、(1)已知等差数列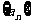 ,
,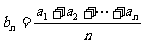 (
(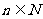 ),求证:
),求证: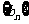 仍为等差数列;
仍为等差数列;
(2)已知等比数列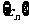 ,
,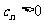 (
(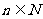 ),类比上述性质,写出一个真命题并加以证明.
),类比上述性质,写出一个真命题并加以证明.
[解析](1)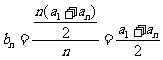 ,
,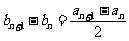 ,
,
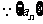 为等差数列
为等差数列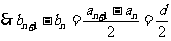 为常数,所以
为常数,所以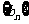 仍为等差数列;
仍为等差数列;
(2)类比命题:若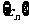 为等比数列,
为等比数列,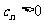 (
(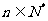 ),
),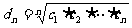 ,则
,则 为等比数列
为等比数列
证明: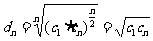 ,
,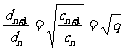 为常数,
为常数, 为等比数列
为等比数列
8、(2008惠州一模)设 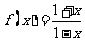 ,又记
,又记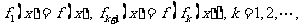 则
则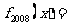 ( )
( )
A.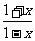 ;
B.
;
B.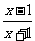 ;
C.
;
C.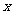 ; D.
; D.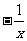 ;
;
[解析]
C 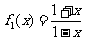 ,
,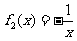 ,
,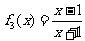 ,
,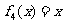 ,
,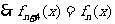
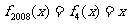
7、(2008汕头一模)设P是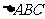 内一点,
内一点,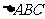 三边上的高分别为
三边上的高分别为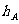 、
、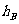 、
、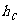 ,P到三边的距离依次为
,P到三边的距离依次为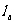 、
、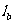 、
、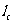 ,则有
,则有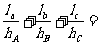 ______________;类比到空间,设P是四面体ABCD内一点,四顶点到对面的距离分别是
______________;类比到空间,设P是四面体ABCD内一点,四顶点到对面的距离分别是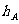 、
、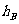 、
、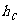 、
、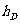 ,P到这四个面的距离依次是
,P到这四个面的距离依次是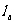 、
、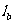 、
、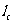 、
、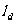 ,则有_________________。
,则有_________________。
[解析]用等面积法可得,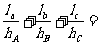 1,类比到空间有
1,类比到空间有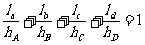
6、类比平面向量基本定理:“如果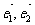 是平面
是平面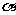 内两个不共线的向量,那么对于平面内任一向量
内两个不共线的向量,那么对于平面内任一向量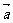 ,有且只有一对实数
,有且只有一对实数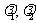 ,使得
,使得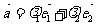 ”,写出空间向量基本定理是:
”,写出空间向量基本定理是:
[解析] 如果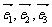 是空间三个不共面的向量,那么对于空间内任一向量
是空间三个不共面的向量,那么对于空间内任一向量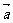 ,有且只有一对实数
,有且只有一对实数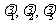 ,使得
,使得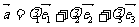
综合提高训练
5、如果函数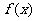 在区间
在区间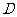 上是凸函数,那么对于区间
上是凸函数,那么对于区间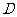 内的任意
内的任意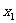 ,
,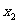 ,…,
,…,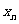 ,
,
都有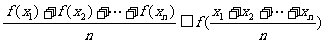 .若
.若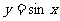 在区间
在区间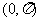 上是凸函数,那么在
上是凸函数,那么在
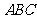 中,
中,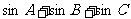 的最大值是________________.
的最大值是________________.
[解析] 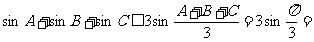
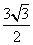
4、如图第n个图形是由正n+2边形“扩展”而来,(n=1,2,3,…)。则第n-2
个图形中共有 个顶点。
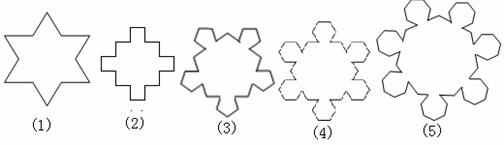
[解析] 设第n个图中有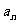 个顶点,则
个顶点,则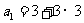 ,
,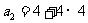 ,
,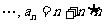 ,
,
3、(华南师大附中2007-2008学年度高三综合测试(三))
给出下面类比推理命题(其中Q为有理数集,R为实数集,C为复数集):
①“若 ”类比推出“
”类比推出“ ”
”
②“若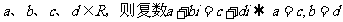 ”类比推出
”类比推出
“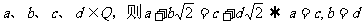 ”
”
③“若 ”类比推出“若
”类比推出“若 ”
”
④“若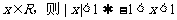 ”类比推出“若
”类比推出“若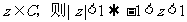 ”
”
其中类比结论正确的个数有 ( )
A.1 B.2 C.3 D.4
[解析] 类比结论正确的只有①
2、命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是
A.使用了归纳推理 B.使用了类比推理
C.使用了“三段论”,但大前提错误 D.使用了“三段论”,但小前提错误
[解析]大前提是特指命题,而小前提是全称命题,故选C
1、对于集合A,B,定义运算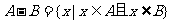 ,则
,则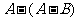 =( )
=( )
A.B
B.A C.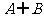 D.
D. 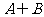
[解析]D [用图示法]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com