11．若直线y＝2a与函数y＝|a^x－1|(a＞0且a≠1)的图象有两个公共点，求a的取值范围．

解：当0＜a＜1时，y＝|a^x－1|的图象如图(1)所示，

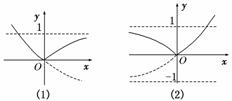
由已知得0＜2a＜1，∴0＜a＜.

当a＞1时，y＝|a^x－1|的图象如图(2)所示，

由已知可得0＜2a＜1，∴0＜a＜，但a＞1，故a∈∅.

综上可知，0＜a＜.

10．已知函数f(x)＝log₂(x+1)，将函数y＝f(x)的图象向左平移一个单位，再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)，得到函数y＝g(x)的图象．求函数y＝g(x)的解析式．

解：由已知，将函数f(x)＝log₂(x+1)的图象向左平移一个单位，得到y＝log₂(x+1+1)的图象，再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)，得到函数y＝g(x)＝2log₂(x+2)的图象．

故g(x)＝2log₂(x+2)．

9．已知定义在[0，+∞)上的函数y＝f(x)和y＝g(x)的图象如图所示，则不等式f(x)·g(x)>0的解集是____________．

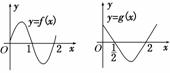
解析：由题图可知，当0<x<时，f(x)>0，g(x)>0；

当<x<1时，f(x)>0，g(x)<0；

当1<x<2时，f(x)<0，g(x)<0，

当x>2时，f(x)>0，g(x)>0，

因此f(x)·g(x)>0的解集是

{x|0<x<，或1<x<2或x>2}．

答案：{x|0<x<，或1<x<2或x>2}

8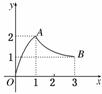．如图，函数f(x)的图象是曲线OAB，其中点O，A，B的坐标分别为(0,0)，(1,2)，(3,1)，则f()的值等于________．

解析：由图象知f(3)＝1，

∴＝1，∴f()＝f(1)＝2.

答案：2

7．为了得到函数f(x)＝log₂x的图象，只需将函数g(x)＝log₂的图象__________________．

解析：g(x)＝log₂＝log₂x－3＝f(x)－3，因此只需将函数g(x)的图象向上平移3个单位即可得到函数f(x)＝log₂x的图象．

答案：向上平移3个单位

6．函数y＝2^|x|的定义域为[a，b]，值域为[1,16]，当a变动时，函数b＝g(a)的图象可以是(　)

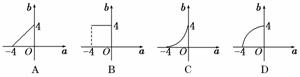
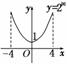解析：由图象知

故b＝g(a)，即为b＝4(－4≤a≤0)．

答案：B

5．若方程f(x)－2＝0在(－∞，0)内有解，则y＝f(x)的图象是(　)

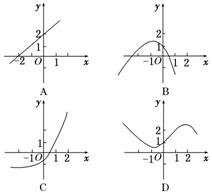
解析：由图可知，只有D中y＝f(x)图象与y＝2图象在x<0时有交点．

答案：D

4．函数y＝ln的图象为(　)

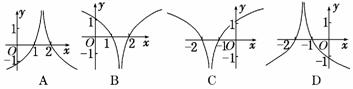
解析：易知2x－3≠0，即x≠，排除C，D项．当x>时，函数为减函数，当x<时，函数为增函数．

答案：A

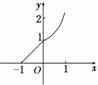
3．已知f(x)＝，则如图中函数的图象错误的是(　)

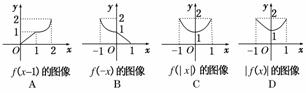
解析：因f(x)＝其图象如图，验证知f(x－1)，f(－x)，f(|x|)的图象均正确，只有|f(x)|的图象错误．

答案：D

2．把函数y＝f(x)＝(x－2)²+2的图象向左平移1个单位，再向上平移1个单位，所得图象对应的函数的解析式是(　)

A．y＝(x－3)²+3　 　　　　　　　　　 B．y＝(x－3)²+1

C．y＝(x－1)²+3　 　　　　　　　　　 D．y＝(x－1)²+1

解析：把函数y＝f(x)的图象向左平移1个单位，即把其中x换成x+1，于是得y＝[(x+1)－2]²+2＝(x－1)²+2，再向上平移1个单位，即得到y＝(x－1)²+2+1＝(x－1)²+3.

答案：C