8．(2010·广州模拟)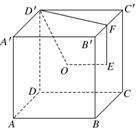如图，点O为正方体ABCD－A′B′C′D′的中心，点E为面B′BCC′的中心，点F为B′C′的中点，则空间四边形D′OEF在该正方体的各个面上的正投影可能是______________(填出所有可能的序号)．

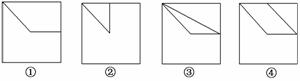
解析：空间四边形D′OEF在正方体的面DCC′D′及其对面ABB′A′上的正投影是①；在面BCC′B′及其对面ADD′A′上的正投影是②；在面ABCD及其对面A′B′C′D′上的正投影是③，故填①②③.

答案：①②③

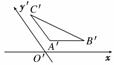
7．(2010·皖南八校)已知三棱锥的直观图及其俯视图与侧(左)视图如下，俯视图是边长为2的正三角形，侧(左)视图是有一直角边为2的直角三角形，则该三棱锥的正(主)视图面积为________．

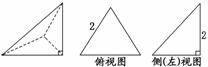
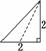解析：三棱锥的正(主)视图如图所示，故正(主)视图的面积为×2×2＝2.

答案：2

6．若某几何体的三视图(单位：cm)如图所示，则此几何体的侧面积等于(　)

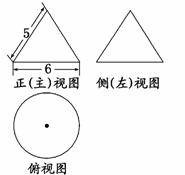
A．12π cm²　 　　　　　　　　　　 B．15π cm²

C．24π cm²　 　　　　　　　　　　 D．30π cm²

答案：B

5．如图△A′B′C′是△ABC的直观图，那么△ABC是(　)

A．等腰三角形

B．直角三角形

C．等腰直角三角形

D．钝角三角形

答案：B

4．(2010·福建高考)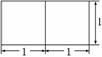若一个底面是正三角形的三棱柱的正(主)视图如图所示，则其侧面积等于　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　 B．2

C．2　 　　　　　　　　　 D．6

解析：由三棱柱的正(主)视图可知此三棱柱为底面边长为2，侧棱长为1的正三棱柱．

∴S_侧＝2×1×3＝6.

答案：D

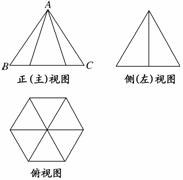
3．(2011·湖南六市联考)一个几何体的三视图如下图所示，其中正(主)视图中△ABC是边长为2的正三角形，俯视图为正六边形，那么该几何体的侧(左)视图的面积为(　)

A.　　　　 B.

C．1　 　　　　　　　　　　　　 D．2

解析：由三视图知该几何体为正六棱锥，底面边长为1，高为.侧(左)视图为等腰三角形，底边边长为，高为，所以侧(左)视图的面积为××＝.

答案：A

2．如图，不是正四面体的表面展开图的是(　)

A．①⑥　　　　　　 B．②⑤

C．③④ 　　　 　　　　　　　　　　 D．④⑤

解析：④⑤不能折成四面体．

答案：D

1．如图所示的几何体(下底面是正六边形)，其侧(左)视图正确的是(　)

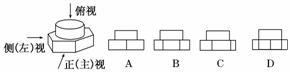
解析：由于几何体的下部为正六面体，故侧(左)视图内只有一条棱．

答案：A

12．(2010·广州模拟)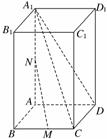在长方体ABCD－A₁B₁C₁D₁中，AB＝BC＝1，AA₁＝2，点M是BC的中点，点N是AA₁的中点．

(1)求证：MN∥平面A₁CD；

(2)过N，C，D三点的平面把长方体ABCD－A₁B₁C₁D₁截成两部分几何体，求所截成的两部分几何体的体积的比值．

解：(1)证明：设点P为AD的中点，连结MP、NP，

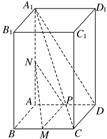∵点M是BC的中点，∴MP∥CD.

∵CD⊂平面A₁CD，MP⊄平面A₁CD，

∴MP∥平面A₁CD.

∵点N是AA₁的中点，

∴NP∥A₁D.

∵A₁D⊂平面A₁CD，NP⊄平面A₁CD，

∴NP∥平面A₁CD.

∵MP∩NP＝P，MP⊂平面MNP，NP⊂平面MNP，

∴平面MNP∥平面A₁CD.∵MN⊂平面MNP，

∴MN∥平面A₁CD.

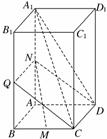
(2)取BB₁的中点Q，连结NQ、CQ、ND，

∵点N是AA₁的中点，

∴NQ∥AB.

∵AB∥CD，∴NQ∥CD，

∴过N、C、D三点的平面NQCD把长方体ABCD－A₁B₁C₁D₁截成两部分几何体，其中一部分几何体为直棱柱QBC－NAD，另一部分几何体为直四棱柱B₁QCC₁－A₁NDD₁，

∴S_△QBC＝·QB·BC＝×1×1＝，

∴直三棱柱QBC－NAD的体积V₁＝S_△QBC·AB＝.

∵长方体ABCD－A₁B₁C₁D₁的体积V＝1×1×2＝2，

∴直四棱柱B₁QCC₁－A₁NDD₁的体积V₂＝V－V₁＝，

∴＝＝，

∴所截成的两部分几何体的体积的比值为.

11．正三棱锥的高为1，底面边长为2，内有一个球与四个面都相切，求棱锥的表面积和球的半径．

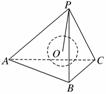
解：过PA与球心O作截面PAE与平面PCB交于PE，与平面ABC交于AE，因△ABC是正三角形，易知AE即是△ABC中BC边上的高，又是BC边上的中线，作为正三棱锥的高PD通过球心，且D是三角形△ABC的重心，据此根据底面边长为2

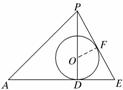，即可算出DE＝AE＝××2＝，

PE＝＝，

由△POF∽△PED，知＝，

∴＝，r＝－2.

∴S_表＝S_侧+S_底＝3××2×+×(2)²＝9+6.