
题目列表(包括答案和解析)
(二)必做题(12-16题)
12.设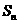 是等差数列
是等差数列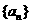
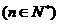 ,的前
,的前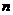 项和,且
项和,且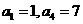 ,则
,则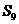 =
.
=
.
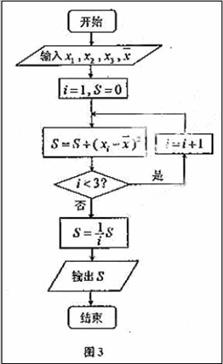
13.若执行如图3所示的框图,输入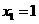 ,
, ,则输出的数等于
。
,则输出的数等于
。
14.在边长为1的正三角形ABC中, 设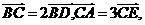 则
则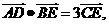 =__________________.
=__________________.
15.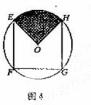 如图4,EFGH
是以O 为圆心,半径为1的圆的内接正方形。将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形EFGH内”,
B表示事件“豆子落在扇形OHE(阴C影部分)内”,则
如图4,EFGH
是以O 为圆心,半径为1的圆的内接正方形。将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形EFGH内”,
B表示事件“豆子落在扇形OHE(阴C影部分)内”,则
(1)P(A)= _____________; (2)P(B|A)= .
16.对于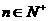 ,将n 表示
,将n 表示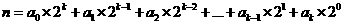 ,当
,当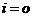 时,
时,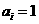 ,当
,当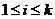 时,
时, 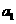 为0或1.记
为0或1.记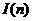 为上述表示中
为上述表示中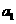 为0的个数(例如:
为0的个数(例如: ),故
),故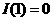 ,
, 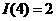 ),则
),则
(1)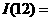 ________________;(2)
________________;(2) 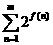 ________________;
________________;
(一)选做题(请考生在9、10、11三题中任选一题作答,如果全做,则按前两题记分)
9.在直角坐标系xOy中,曲线C1的参数方程为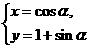 (
(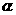 为参数)在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,曲线C2的方程为
为参数)在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,曲线C2的方程为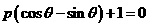 ,则C1与C2的交点个数为
,则C1与C2的交点个数为
10. 设
设 ,则
,则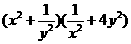 的最小值为
。
的最小值为
。
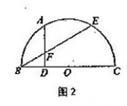
11.如图2,A,E是半圆周上的两个三等分点,直径BC=4,
AD⊥BC,垂足为D,BE与AD相交与点F,则AF的长为 。
1.若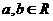 ,
,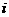 为虚数单位,且
为虚数单位,且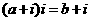 则
则
A.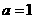 ,
,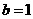 B.
B. 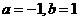 C.
C.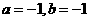 D.
D. 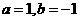
2.设集合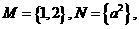 则 “
则 “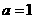 ”是“
”是“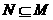 ”的
”的
A.充分不必要条件 B.必要不充分条件
C. 充分必要条件 D. 既不充分又不必要条件
3.设图1是某几何体的三视图,则该几何体的体积为
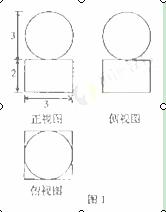
A. 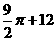
B. 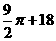
C. 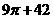
D. 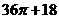
4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
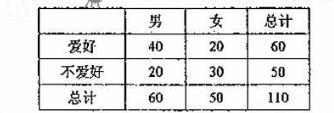
由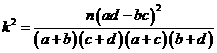 算得,
算得,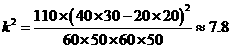 .
.

参照附表,得到的正确结论是
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
5.设双曲线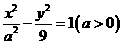 的渐近线方程为
的渐近线方程为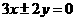 ,则
,则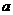 的值为
的值为
A.4 B.3 C.2 D.1
6.由直线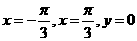 与曲线
与曲线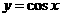 所围成的封闭图形的面积为
所围成的封闭图形的面积为
A. 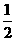 B.1
C.
B.1
C. 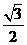 D.
D.
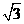
7.设m>1,在约束条件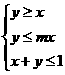 下,目标函数Z=x+my的最大值小于2,则m 的取值范围为
下,目标函数Z=x+my的最大值小于2,则m 的取值范围为
A.(1,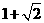 ) B.(
) B.(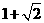 ,
, ) C.(1,3 ) D.(3,
) C.(1,3 ) D.(3, )
)
8.设直线x=t 与函数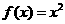
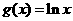 的图像分别交于点M,N,则当
的图像分别交于点M,N,则当 达到最小时t的值为
达到最小时t的值为
A.1
B. 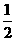 C.
C.
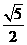 D.
D.
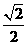
填空题:本大题共8小题,考生作答7小题,每小题5分,共35分,把答案填在答题卡中对应号后的横线上。
21.(本小题满分14分)
设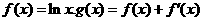 。
。
(Ⅰ)求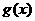 的单调区间和最小值;
的单调区间和最小值;
(Ⅱ)讨论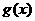 与
与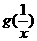 的大小关系;
的大小关系;
(Ⅲ)求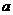 的取值范围,使得
的取值范围,使得 <
<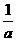 对任意
对任意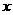 >0成立。
>0成立。
解(Ⅰ)由题设知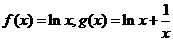 ,
,
∴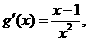 令
令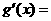 0得
0得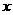 =1,
=1,
当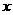 ∈(0,1)时,
∈(0,1)时,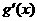 <0,故(0,1)是
<0,故(0,1)是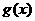 的单调减区间。
的单调减区间。
当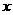 ∈(1,+∞)时,
∈(1,+∞)时,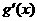 >0,故(1,+∞)是
>0,故(1,+∞)是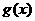 的单调递增区间,因此,
的单调递增区间,因此,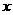 =1是
=1是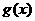 的唯一值点,且为极小值点,从而是最小值点,所以最小值为
的唯一值点,且为极小值点,从而是最小值点,所以最小值为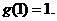
(II)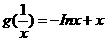
设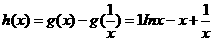 ,则
,则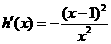 ,
,
当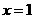 时,
时,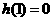 即
即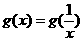 ,
,
当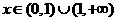 时
时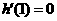 ,
,
因此,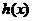 在
在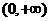 内单调递减,
内单调递减,
当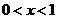 时,
时,
即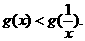
(III)由(I)知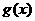 的最小值为1,所以,
的最小值为1,所以,
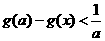 ,对任意
,对任意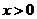 ,成立
,成立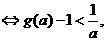
即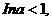 从而得
从而得 。
。
20. (本小题满分13分)
(本小题满分13分)
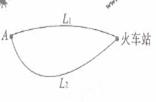
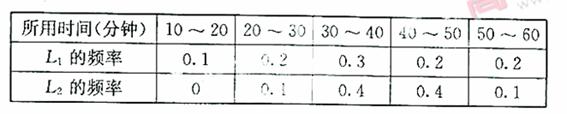
如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下:

(Ⅰ)试估计40分钟内不能赶到火车站的概率;
(Ⅱ )分别求通过路径L1和L2所用时间落在上表中各时间段内的频率;
(Ⅲ )现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站,为了尽量大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的 路径。
解(Ⅰ)由已知共调查了100人,其中40分钟内不能赶到火车站的有12+12+16+4=44人,
 用频率估计相应的概率为0.44.
用频率估计相应的概率为0.44.
(Ⅱ )选择L1的有60人,选择L2的有40人,
故由调查结果得频率为:
( Ⅲ )A1,A2,分别表示甲选择L1和L2时,在40分钟内赶到火车站;
B1,B2分别表示乙选择L1和L2时,在50分钟内赶到火车站。
由(Ⅱ)知P(A1) =0.1+0.2+0.3=0.6
P(A2)=0.1+0.4=0.5, P(A1)>P(A2)
 甲应选择L1
甲应选择L1
P(B1) =0.1+0.2+0.3+0.2=0.8
P(B2)=0.1+0.4+0.4=0.9,P(B2)>P(B1),
∴ 乙应选择L2.
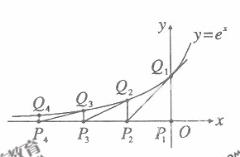
19.(本小题满分12分)
如图,从点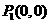 做x轴的垂线交曲线
做x轴的垂线交曲线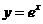 于点
于点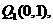 曲线在
曲线在 点处的切线与x轴交于点
点处的切线与x轴交于点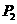 ,再从
,再从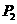 做x轴的垂线交曲线于点
做x轴的垂线交曲线于点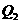 ,依次重复上述过程得到一系列点:
,依次重复上述过程得到一系列点: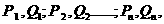 记
记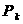 点的坐标为
点的坐标为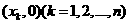 .
.
(Ⅰ)试求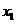 与
与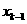 的关系
的关系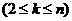
( Ⅱ)求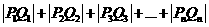
解(Ⅰ)设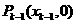 ,由
,由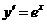 得
得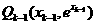 点处切线方程为
点处切线方程为
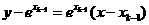
由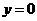 得
得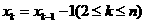 。
。
( Ⅱ) ,得
,得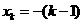 ,
,
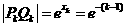
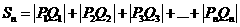
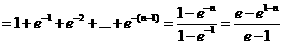
18.(本小题满分12分)
叙述并证明余弦定理。
解 余弦定理:三角形任何一边的平方等于其他两遍平方的和减去这两边与它们夹角的余弦之积的两倍。或:在△ABC中,a,b,c为A,B,C的对边,有
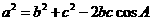 ,
,
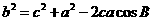 ,
,
 .
.
证法一 如图,
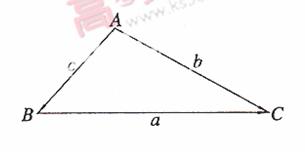
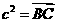
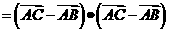
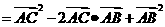


即
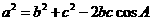
同理可证
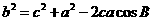 ,
,

证法二 已知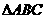 中
中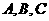 所对边分别为
所对边分别为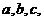 ,以
,以 为原点,
为原点,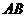 所在直线为
所在直线为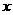 轴建立直角坐标系,则
轴建立直角坐标系,则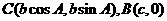 ,
,
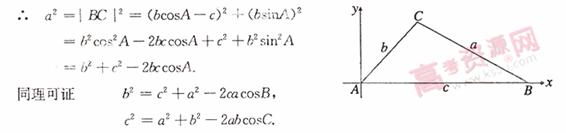
P. (本小题满分12分)
如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD高,沿AD把是BC上的△ABD折起,使∠BDC=90°。
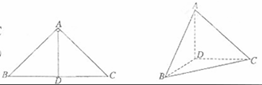
(Ⅰ)证明:平面ADB ⊥平面BDC;
(Ⅱ )设BD=1,求三棱锥D-ABC的表面积。
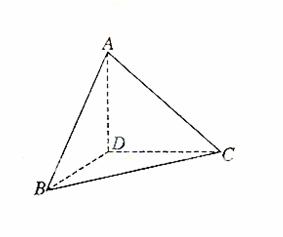
解(Ⅰ)∵折起前AD是BC边上的高,
∴ 当Δ ABD折起后,AD⊥DC,AD⊥DB,
又DB DC=D,
DC=D,
∴AD⊥平面BDC,
∵AD 平面 平面BDC.
平面BDC.
(Ⅱ)由(Ⅰ)知,DA ,
, ,
,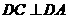 ,
,
 DB=DA=DC=1,
DB=DA=DC=1,
 AB=BC=CA=
AB=BC=CA=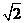 ,
,
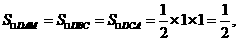
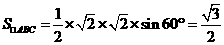
表面积: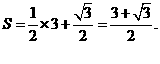
17.(本小题满分12分)
设椭圆C: 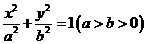 过点(0,4),离心率为
过点(0,4),离心率为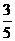
(Ⅰ)求C的方程;
(Ⅱ)求过点(3,0)且斜率为 的直线被C所截线段的中点坐标
的直线被C所截线段的中点坐标
解(Ⅰ)将(0,4)代入C的方程得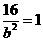 ∴b=4
∴b=4
又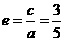 得
得
即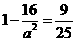 , ∴a=5
, ∴a=5
∴C的方程为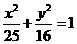
( Ⅱ)过点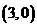 且斜率为
且斜率为 的直线方程为
的直线方程为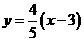 ,
,
设直线与C的交点为A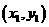 ,B
,B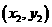 ,
,
将直线方程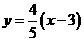 代入C的方程,得
代入C的方程,得
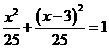 ,
,
即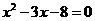 ,解得
,解得
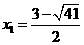 ,
,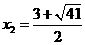 ,
,
 AB的中点坐标
AB的中点坐标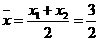 ,
,
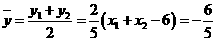 ,
,
即中点为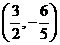 。
。
注:用韦达定理正确求得结果,同样给分。
15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
A.(不等式选做题)若不等式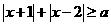 对任意
对任意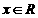 恒成立,则a的取值范围是__________。
恒成立,则a的取值范围是__________。
B.(几何证明选做题)如图,
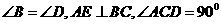
且AB=6,AC+4,AD+12,则AE=_______.
 C. (坐标系与参数方程选做题)直角坐标系xoy中,以原点为极点,x轴的正半轴为极轴建极坐标系,设点A,B分别在曲线
C. (坐标系与参数方程选做题)直角坐标系xoy中,以原点为极点,x轴的正半轴为极轴建极坐标系,设点A,B分别在曲线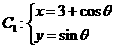 (
(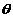 为参数)和曲线
为参数)和曲线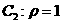 上,则
上,则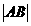 的最小值为________.
的最小值为________.
14. 设n∈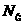 ,一元二次方程
,一元二次方程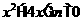 有整数根的充要条件是n=_____.
有整数根的充要条件是n=_____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com