7．函数y＝－(x－3)|x|的递增区间是________．

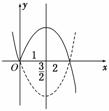解析：y＝－(x－3)|x|

＝

作出该函数的图象，观察图象知递增区间为[0，]．

答案：[0，]

6．已知定义在R上的奇函数f(x)满足f(1+x)＝f(1－x)，且f(x)在区间[3,5]上单调递增，则函数f(x)在区间[1,3]上的(　)

A．最大值是f(1)，最小值是f(3)

B．最大值是f(3)，最小值是f(1)

C．最大值是f(1)，最小值是f(2)

D．最大值是f(2)，最小值是f(3)

解析：依题意得f(x)的图象关于直线x＝1对称，f(x+1)＝－f(x－1)，f(x+2)＝－f(x)，f(x+4)＝－f(x+2)＝f(x)，即函数f(x)是以4为周期的函数．由f(x)在[3,5]上是增函数与f(x)的图象关于直线x＝1对称得，f(x)在[－3，－1]上是减函数．又函数f(x)是以4为周期的函数，因此f(x)在[1,3]上是减函数，f(x)在[1,3]上的最大值是f(1)，最小值是f(3)．

答案：A

5．定义在R上的偶函数f(x)满足：对任意x₁，x₂∈[0，+∞)(x₁≠x₂)，有<0，则(　)

A．f(3)<f(－2)<f(1)　 　　　　　　　　　　　 B．f(1)<f(－2)<f(3)

C．f(－2)<f(1)<f(3) 　 　　　　　　　　　　 D．f(3)<f(1)<f(－2)

解析：对任意x₁，x₂∈[0，+∞)(x₁≠x₂)，有<0，实际上等价于函数f(x)在[0，+∞)上是减函数，故f(3)<f(2)<f(1)，由于函数是偶函数，故f(3)<f(－2)<f(1)．

答案：A

4．定义新运算⊕：当a≥b时，a⊕b＝a；当a<b时，a⊕b＝b²，则函数f(x)＝(1⊕x)x－(2⊕x)，x∈[－2,2]的最大值等于(　)

A．－1　 　　　　　　　　　　 B．1

C．6　 　　　　　　　　　　　　 D．12

解析：由题意知

当－2≤x≤1时，f(x)＝x－2，

当1＜x≤2时，f(x)＝x³－2，

又∵f(x)＝x－2，f(x)＝x³－2在定义域上都为增函数，

∴f(x)的最大值为f(2)＝2³－2＝6.

答案：C

3．已知函数f(x)为R上的减函数，则满足f(|x|)<f(1)的实数x的取值范围是(　)

A．(－1,1)　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．(0,1)

C．(－1,0)∪(0,1)　 　　 　　　　　　　　　　　　　　　　　 D．(－∞，－1)∪(1，+∞)

解析：∵f(x)为R上的减函数，且f(|x|)<f(1)，

∴|x|>1，∴x<－1或x>1.

答案：D

2．函数y＝2x²－(a－1)x+3在(－∞，1]内递减，在(1，+∞)内递增，则a的值是(　)

A．1　 　　　　　　　　　　　　 B．3

C．5　 　　　　　　　　　　　　 D．－1

解析：依题意可得对称轴x＝＝1，∴a＝5.

答案：C

1．(2010·大连模拟)下列函数在(0,1)上是减函数的是(　)

A．y＝log_0.5(1－x)　 　　　　　　　　 B．y＝x^0.5

C．y＝0.5^1－x　 　　　　　　　　　　　　 D．y＝(1－x²)

解析：y＝log_0.5(1－x)在(0,1)上为增函数；

y＝x^0.5在(0,1)上是增函数；

y＝0.5^1－x在(0,1)上为增函数；

函数y＝(1－x²)在(－∞，0)上为增函数，在(0，+∞)上为减函数，

∴函数y＝(1－x²)在(0,1)上是减函数．

答案：D

12．设f(x)是定义在R上的奇函数，且对任意实数x，恒有f(x+2)＝－f(x)．当x∈[0,2]时，f(x)＝2x－x².

(1)求证：f(x)是周期函数；

(2)当x∈[2,4]时，求f(x)的解析式；

(3)计算f(0)+f(1)+f(2)+…+f(2 012)．

解：(1)∵f(x+2)＝－f(x)，

∴f(x+4)＝－f(x+2)＝f(x)．

∴f(x)是周期为4的周期函数．

(2)当x∈[－2,0]时，－x∈[0,2]，由已知得

f(－x)＝2(－x)－(－x)²＝－2x－x²，

又f(x)是奇函数，∴f(－x)＝－f(x)＝－2x－x²，

∴f(x)＝x²+2x.

又当x∈[2,4]时，x－4∈[－2,0]，

∴f(x－4)＝(x－4)²+2(x－4)．

又f(x)是周期为4的周期函数，

∴f(x)＝f(x－4)

＝(x－4)²+2(x－4)

＝x²－6x+8.

从而求得x∈[2,4]时，f(x)＝x²－6x+8.

(3)f(0)＝0，f(2)＝0，

f(1)＝1，f(3)＝－1.

又f(x)是周期为4的周期函数，

∴f(0)+f(1)+f(2)+f(3)＝f(4)+f(5)+f(6)+f(7)＝…＝f(2 008)+f(2 009)+f(2 010)+f(2 011)+f(2 012)＝0.

∴f(0)+f(1)+f(2)+…+f(2 012)＝0.

11．已知函数f(x)＝是奇函数．

(1)求实数m的值；

(2)若函数f(x)在区间[－1，a－2]上单调递增，求实数a的取值范围．

解：(1)设x<0，则－x>0，

所以f(－x)＝－(－x)²+2(－x)＝－x²－2x.

又f(x)为奇函数，所以f(－x)＝－f(x)，

于是x<0时，f(x)＝x²+2x＝x²+mx，所以m＝2.

(2)要使f(x)在[－1，a－2]上单调递增，

结合f(x)的图象知

所以1＜a≤3，故实数a的取值范围是(1,3]．

10．判断下列函数的奇偶性．

(1)f(x)＝；

(2)f(x)＝

解：(1)由得定义域为(－1,0)∪(0,1)，这时f(x)＝＝－.

∵f(－x)＝－＝－＝f(x)．

∴f(x)为偶函数．

(2)当x<0时，－x>0，

则f(－x)＝－(－x)²－x＝－(x²+x)＝－f(x)

当x>0时，－x<0，则f(－x)＝(－x)²－x＝x²－x＝－(－x²+x)＝－f(x)

∴对任意x∈(－∞，0)∪(0，+∞)都有f(－x)＝－f(x)

故f(x)为奇函数．