
题目列表(包括答案和解析)
4.已知向量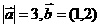 ,且
,且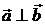 ,则
,则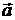 的坐标是___________
的坐标是___________
例5(投影的概念)若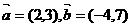 ,求
,求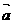 在
在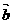 方向上的投影
方向上的投影
例6(数量积的性质的应用)若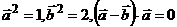 , 求
, 求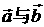 的夹角
的夹角
练习:1.若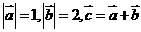 ,且
,且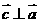 ,则向量
,则向量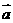 与向量
与向量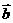 的夹角为 ( )
的夹角为 ( )
A. 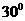 B.
B.
 C.
C. 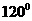 D.
D.

3.若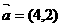 ,则与
,则与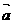 垂直的单位向量的坐标是
垂直的单位向量的坐标是
2.若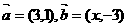 ,且
,且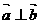 ,则实数
,则实数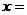
4.判断下列各题是否正确
(1)若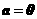 ,则对任意向量
,则对任意向量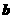 ,有
,有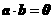
(2)若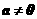 ,则对任意非零量
,则对任意非零量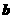 ,有
,有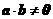
(3)若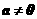 ,且
,且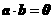 ,则
,则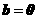
(4)若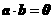 ,则
,则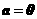 或
或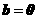
(5)对任意向量 有
有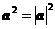
(6)若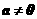 ,且
,且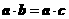 ,则
,则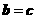
例2 (易错点)已知△ABC中,a=5,b=8,C=60°,求
(易错点)已知△ABC中,a=5,b=8,C=60°,求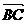 ·
· .
.
总结:这一类型题,要求学生确实把握好数量积的定义、性质、运算律.
例3 (数量积公式的应用)已知|a|=3,|b|=6,当①a∥b,②a⊥b,③a与b的夹角是60°时,分别求a·b.
总结:两个向量的数量积与它们的夹角有关,其范围是[0°,180°],因此,当a∥b时,有0°或180°两种可能.
例4(数量积的坐标表示的应用、模长公式的应用、向量夹角公式)已知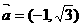 ,
,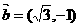 ,求
,求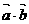 ,
,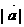 ,
,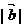 ,
,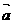 与
与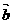 的夹角
的夹角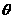 .
.
练习:1.若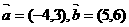 ,则
,则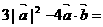
3.下列说法中正确的序号是( )
①一个平面内只有一对不共线的向量可作为基底;
②两个非零向量平行,则他们所在直线平行;
③零向量不能作为基底中的向量;
④两个单位向量的数量积等于零。
(A)①③ (B)②④ (C)③ (D)②③
例1 判断正误(易错点)
①a·0=0;②0·a=0;③|a·b|=|a||b|;④若a≠0,则对任一非零b有a·b≠0;⑤a·b=0,则a与b中至少有一个为0;⑥对任意向量a,b,с都有(a·b)с=a(b·с);⑦a与b是两个单位向量,则a2=b2 ⑧
⑧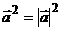
总结:实数中的好多结论在向量中是不成立的。如:
⑴ 若
若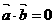 ,则
,则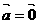 或
或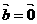 ;
;
⑵若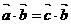 ,且
,且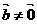 ,则
,则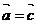 ;
;
⑶若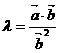 ,则
,则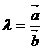 ;
;
⑷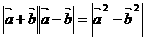 ;
;
⑸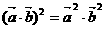
⑹若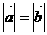 ,则
,则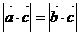
练习:1.下列命题中真命题是( )
(A) 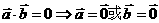 (B)
(B) 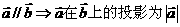
(C) 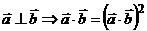 (D)
(D)
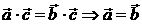
2.下面给出的关系式中正确的个数是( )
① 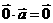 ②
②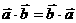 ③
③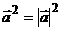 ④
④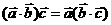 ⑤
⑤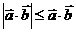
(A) 0 (B) 1 (C) 2 (D) 3
4、x是什么实数时,函数y = - x2 + 5x + 14的值是
(1)0 (2)正数 (3)负数
3、解下列不等式
(1)- 6x2 – x + 2 < 0 (2)1 – 4x2 > 4x + 2
(3)1 – 3x < x2 (4)(x – 2)(x + 2) > 1
2、解下列不等式
(1)2x2 – 5x + 3 < 0 (2)3x2 – x – 4 > 0
(3)2x2 + 4x + 3 > 0 (4)9x2 – 6x + 1≤0
1、不等式(x – 1)(x – 3) > 0的解集为( )
A {x|x < 1} B {x|x > 3}
C {x|x < 1或x > 3} D {x| 1 < x < 3}
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com