6.会综合运用二次函数图像和性质解决有关问题。

[知识再现]

5.进一步掌握二次函数的图像和性质。

4.掌握研究二次函数图像和性质的配方法。

3.二次函数的图像的顶点坐标、对称轴方程、单调区间和最值的求法。

2.二次函数的图像的画法。

1.二次函数的一般方法--配方法。

2.2.2 二次函数的性质与图象 学案

[预习要点及要求]

5．课后作业：

(1)

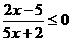
(2)(1-2x)(x-1)(x+2)< 0

(3)(x+1)(-2x+3)(3x+1)> 0

(4)(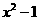)()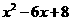0

(5)

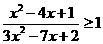
4．课堂练习：解下列不等式：

　(1)

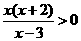
(2)

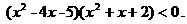
引例：解一元二次不等式(x+3)(x-1)<0

例1：解不等式：(x-1)(x+4)(x-3)>0；

练习：解不等式：(1)(x+1)(x-2)(x+3)(x-4)>0

练习：用穿轴法解不等式(x+1)(x-2)(x+3)(x-4)>0

例2．解不等式：.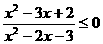

3．课堂小结：

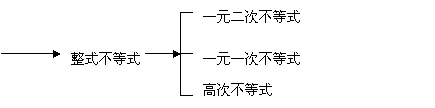分

式

不

等

式