
题目列表(包括答案和解析)
2.填空:(1)方程kx2+4x-1=0的两根之和为-2,则k= .
(2)方程2x2-x-4=0的两根为α,β,则α2+β2= .
(3)方程2x2+2x-1=0的两根为x1和x2,则| x1-x2|= .
1.选择
(1)已知关于x的方程x2+kx-2=0的一个根是1,则它的另一个根是( )
(A)-3 (B)3 (C)-2 (D)2
(2)下列四个说法:
①方程x2+2x-7=0的两根之和为-2,两根之积为-7;
②方程x2-2x+7=0的两根之和为-2,两根之积为7;
③方程3 x2-7=0的两根之和为0,两根之积为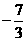 ;
;
④方程3 x2+2x=0的两根之和为-2,两根之积为0.其中正确说法的个数是 ( )
(A)1个 (B)2个 (C)3个 (D)4个
(3)已知一个直角三角形的两条直角边长恰好是方程2x2-8x+7=0的两根,则这个直角三角形的斜边长等于( )
(A)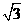 (B)3
(C)6
(D)9
(B)3
(C)6
(D)9
(4)若x1,x2是方程2x2-4x+1=0的两个根,则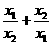 的值为
( )
的值为
( )
(A)6
(B)4 (C)3
(D)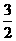
例1 已知方程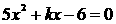 的一个根是2,求它的另一个根及k的值.
的一个根是2,求它的另一个根及k的值.
例2 已知关于x的方程x2+2(m-2)x+m2+4=0有两个实数根,并且这两个实数根的平方和比两个根的积大21,求m的值.
例3 已知两个数的和为4,积为-12,求这两个数.
推论1:
以两个数x1,x2为根的一元二次方程(二次项系数为1)是x2-(x1+x2)x+x1·x2=0.
练习:以-3和1为根的一元二次方程是 .
例4 若x1和x2分别是一元二次方程2x2+5x-3=0的两根.
(1)求| x1-x2|的值;
(2)求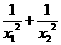 的值; (3)x13+x23.
的值; (3)x13+x23.
练习:(1)若方程x2-3x-1=0的两根分别是x1和x2,则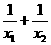 =
.
=
.
(2)已知方程x2-3x-1=0的两根为x1和x2,求(x1-3)( x2-3)的值.
推论2:
若x1和x2分别是一元二次方程ax2+bx+c=0(a≠0),则| x1-x2|=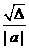 (其中Δ=b2-4ac).
(其中Δ=b2-4ac).
例5 若关于x的一元二次方程x2-x+a-4=0的一根大于零、另一根小于零,求实数a的取值范围.
如果ax2+bx+c=0(a≠0)的两根分别是x1,x2,那么x1+x2=_______;x1·x2=_______.
这一关系也被称为韦达定理
证明:
(1)方程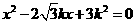 的根的情况是
的根的情况是
(2)若关于x的方程mx2+ (2m+1)x+m=0有两个不相等的实数根,则m的取值范围是 ( )
(A)m<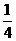 (B)m>-
(B)m>-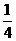 (C)m<
(C)m<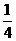 ,且m≠0 (D)m>-
,且m≠0 (D)m>-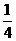 ,且m≠0
,且m≠0
3.2 根与系数的关系(韦达定理)
对于一元二次方程ax2+bx+c=0(a≠0),有
(1)
当Δ>0时,方程有两个不相等的实数根 x1,2=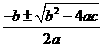 ;
;
(2)
当Δ=0时,方程有两个相等的实数根 x1=x2=-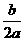 ;
;
(3) 当Δ<0时,方程没有实数根.
例1 判定下列关于x的方程的根的情况(其中a为常数),如果方程有实数根,写出方程的实数根.(1)x2-3x+3=0; (2)x2-ax-1=0;
(3) x2-ax+(a-1)=0; (4)x2-2x+a=0.
练习:1、a为何值时方程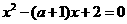 (1)有实数根?(2)没有实数根?
(1)有实数根?(2)没有实数根?
2、解方程
(1)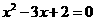 (2)
(2)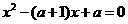
我们知道,对于一元二次方程ax2+bx+c=0(a≠0),用配方法可以将其变形为
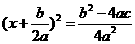 .
①
.
①
一元二次方程ax2+bx+c=0(a≠0)的根的情况可以由b2-4ac来判定,我们把b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)的根的判别式,通常用符号“Δ”来表示.
3.1 一元二次方程及根的判别式
4.解下列方程: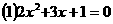
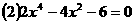
第三节 一元二次方程
3.分解因式:⑴x2+x-(a2-a)
⑵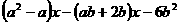
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com