
题目列表(包括答案和解析)
2.已知函数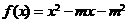 ,则
,则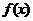 ( )
( )
A.有一个零点 B.有两个零点
C.有一个或两个零点 D.无零点
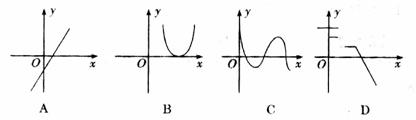
1.下列函数中,不能用二分法求零点的是( )
[考题1]若一次函数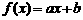 有一个零点2,则二次函数
有一个零点2,则二次函数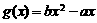 的零点是 。
的零点是 。
[解析]因为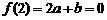 ,所以
,所以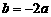 ,从而
,从而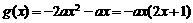 ,令
,令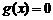 ,解得二次函数
,解得二次函数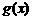 的零点0和
的零点0和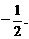
[考题2]求函数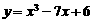 的零点。
的零点。
解:因为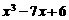
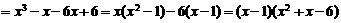
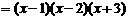 ,
,
令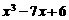
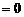 ,解得
,解得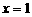 ,或2,或
,或2,或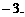
所以函数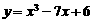 的零点为
的零点为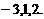
[点评]一次函数的零点是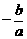 ;二次函数的零点可通过分解因式或求根公式求出;三次函数的零点一般是通过分解因式求得。
;二次函数的零点可通过分解因式或求根公式求出;三次函数的零点一般是通过分解因式求得。
[考题3]若方程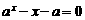 有两个根,则
有两个根,则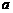 的取值范围是( )
的取值范围是( )
 A.
A.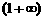 B.
B.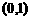
C.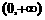 D.
D.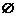
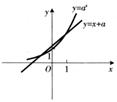
解析:原方程移项得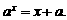
当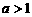 时,在同一直角坐标系内作出函数
时,在同一直角坐标系内作出函数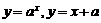 的图象,如图,由图观察得原方程有两个根,从而排除D。
的图象,如图,由图观察得原方程有两个根,从而排除D。
当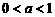 时,在同一直角坐标系内作出函数
时,在同一直角坐标系内作出函数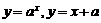 的图象,如图,由图观察得原方程只有一个根,从而排除B。
的图象,如图,由图观察得原方程只有一个根,从而排除B。
又当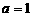 时,原方程为
时,原方程为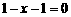 ,解得
,解得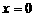 ,只有一个根,从而排除C。
,只有一个根,从而排除C。
故选A。
[点评]本题通过构造函数,利用数形结合解决问题,是方程与函数思想的典性题目。
[考题4]无论 取哪个实数值,函数
取哪个实数值,函数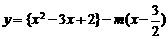 的零点个数都是( )
的零点个数都是( )
 A.1 B.2 C.3 D.不确定
A.1 B.2 C.3 D.不确定
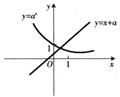
[解析]函数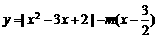 的零点个数即为方程
的零点个数即为方程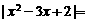
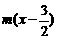 的实根个数,进一步转化为函数
的实根个数,进一步转化为函数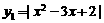 和
和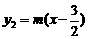 的图象的交点个数。如图,不论
的图象的交点个数。如图,不论 为何值,直线
为何值,直线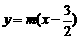 恒过点
恒过点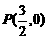 ,两个函数的图象总有2个不同的交点,所以函数
,两个函数的图象总有2个不同的交点,所以函数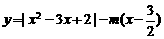 的零点个数是2,故选B。
的零点个数是2,故选B。
[点评]本题的关键是把函数的零点先转化为对应方程的解,再进一步转化为两个函数的图象的交点,然后利用数形结合法求解。
[考点5]设函数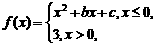 若
若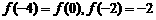 ,则函数
,则函数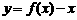 的零点的个数为( )
的零点的个数为( )
A.1 B.2 C.3 D.4
[解析]因为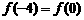 ,所以抛物线
,所以抛物线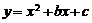 的对称轴为
的对称轴为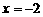 ,即
,即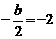 ,解得
,解得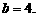
又因为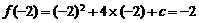 ,解得
,解得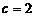 ,所以
,所以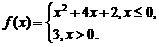
函数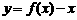 的零点即为方程
的零点即为方程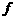
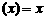 等价于
等价于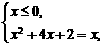 或
或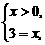 解得
解得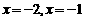 或
或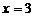 ,所以函数
,所以函数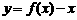 的零点是:
的零点是: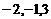 ,共3个,故选C。
,共3个,故选C。
[点评]求分段函数的零点需进行分段讨论,或通过画图象,求图象与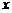 轴的交点。含绝对值的函数一般先去掉绝对值,使其转化为分段函数,再求零点。
轴的交点。含绝对值的函数一般先去掉绝对值,使其转化为分段函数,再求零点。
[考点6]已知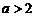 ,且函数
,且函数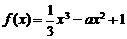 在区间
在区间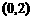 上是减函数,则方程
上是减函数,则方程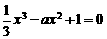 在区间
在区间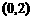 上的实根个数为( )
上的实根个数为( )
A.0 B.1 C.2 D.3
[解析]因为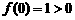 ,
,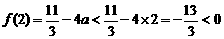 ,即
,即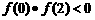 ,所以函数
,所以函数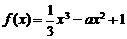 在区间
在区间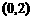 上有零点。
上有零点。
又因为函数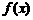 在
在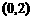 上是减函数,
上是减函数,
所以函数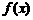 在区间
在区间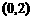 上有且只有一个零点,即方程
上有且只有一个零点,即方程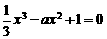 在区间
在区间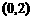 上只有一个实根。故选B。
上只有一个实根。故选B。
[点评]若函数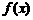 在
在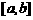 上的图象不间断,且
上的图象不间断,且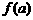 ·
·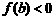 ,则
,则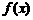 在区间
在区间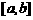 上一定存在零点;若函数
上一定存在零点;若函数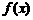 在
在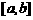 上的图象不间断,且
上的图象不间断,且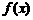 是单调函数,
是单调函数,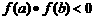 ,则
,则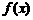 在区间
在区间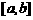 上一定存在唯一的零点。
上一定存在唯一的零点。
[考题7]函数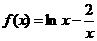 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A.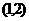 B.
B.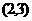 C.
C.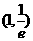 和
和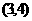 D.
D.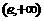
[解析]从已知的区间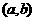 ,求
,求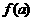 和
和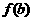 判断是否有
判断是否有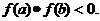
∵ ∴在
∴在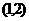 内
内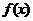 无零点,故排除A. 又
无零点,故排除A. 又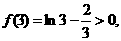
∴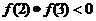 . ∴
. ∴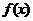 在
在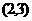 内有一个零点.
内有一个零点.
故选B。
[点评]这是最基本的题型,所用的方法也是基本方法:只要判断区间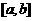 的端点值的乘积是否有
的端点值的乘积是否有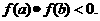
[考题8]求方程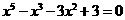 的无理根(精确到0.01).
的无理根(精确到0.01).
[解析]由于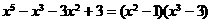 ,所以原方程有两个有理根1和-1,而其无理根是方程
,所以原方程有两个有理根1和-1,而其无理根是方程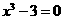 的根,令
的根,令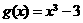 ,以下用二分法求
,以下用二分法求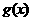 的近似零点。
的近似零点。
由于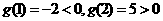 ,故可取
,故可取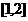 作为计算的初始区间,列表如下:
作为计算的初始区间,列表如下:
|
区间 |
中点 |
中点函数值 |
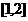 |
1.5 |
0.375 |
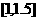 |
1.25 |
-1.047 |
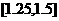 |
1.375 |
-0.4004 |
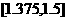 |
1.4375 |
-0.0295 |
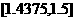 |
1.46875 |
0.1684 |
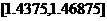 |
1.45312 |
0.06835 |
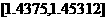 |
1.45031 |
0.05064 |
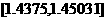 |
1.4439 |
0.0103 |
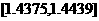 |
|
|
由于区间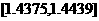 的长度1.4439-1.4375=0.0064<0.01,所以这个区间的两个端点均可作为函数
的长度1.4439-1.4375=0.0064<0.01,所以这个区间的两个端点均可作为函数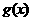 零点的近似值,取其近似值为1.44,因此原方程的无理根是1.44.因此原方程的无理根是1.44.
零点的近似值,取其近似值为1.44,因此原方程的无理根是1.44.因此原方程的无理根是1.44.
[点评]求方程的无理根问题可以通过因式分解,发现其有理根,然后转化为求另一函数的无理根零点的问题,再利用二分法求其零点的近似值。
[考题9]已知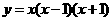 的图象如图所示,因考虑
的图象如图所示,因考虑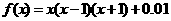 ,则方程式
,则方程式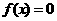 ( )
( )
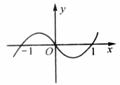 A.有三个实根
A.有三个实根
B.当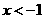 时,恰有一实根
时,恰有一实根
C.当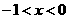 时,恰有一实根
时,恰有一实根
D.当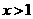 时,恰有一实根
时,恰有一实根
[解析]∵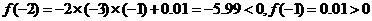 ,即
,即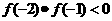 ,
,
∴在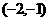 内有一个实根,即方程在
内有一个实根,即方程在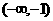 上,恰有一个实根,故B正确。
上,恰有一个实根,故B正确。
又∵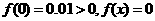 在
在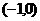 上没有实数根,
上没有实数根,
∴C不正确.
又∵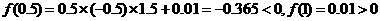 ,即
,即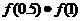 <0,所以
<0,所以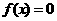 在
在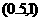 上必有一个实数根,且
上必有一个实数根,且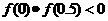 ,∴
,∴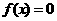 在
在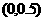 上也有一个实根。
上也有一个实根。
∴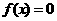 在
在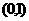 上有两个实根,故D不正确,由
上有两个实根,故D不正确,由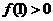 知,
知,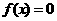 在
在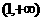 上没有实根。
上没有实根。
∴E不正确,并且由此可知A正确。
[答案]A、B
[点评]解答这类多项选择题的方法与解决单项选择题的方法不同,须逐项验证才可选出该选的答案,并且解单项选择时所用的排除法已不能使用。
6.用二分法求函数零点的近似值的探究
在应用二分法求函数的变号零点的近似值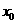 时,从精确度出发,确定需经过多次取区间
时,从精确度出发,确定需经过多次取区间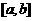 的中点找到零点的近似值,使其达到精确度的要求。
的中点找到零点的近似值,使其达到精确度的要求。
注意:这里指的精确度是指区间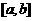 的长度。
的长度。
5、二分法,就是通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步副近零点,进而得到零点近似值的方法。
用二分法求函数零点近似值时,最好是将计算过程中所得到的各个区间、中点坐标、区间中点的函数值等列在一个表格中,这样可以更清楚地发现零点所在的区间。
4.函数零点具有的性质
注意:①函数是否有零点是针对方程是否有实数根而言的,若方程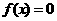 没有实数根,则函数
没有实数根,则函数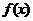 没有零点。
没有零点。
3.函数零点与方程的根的关系
根据函数零点的定义可知:函数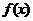 的零点,就是方程
的零点,就是方程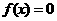 的根,因此判断一个函数是否有零点,有几个零点,就是判断方程
的根,因此判断一个函数是否有零点,有几个零点,就是判断方程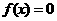 是否有实数根,有几个实数根。
是否有实数根,有几个实数根。
函数零点的求法:解方程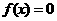 ,所得实数根就是
,所得实数根就是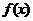 的零点。
的零点。
2、函数零点的判断
如果函数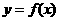 在区间
在区间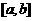 上的图象是连续不断的曲线,并且有
上的图象是连续不断的曲线,并且有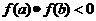 ,那么,函数
,那么,函数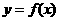 在区间
在区间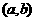 内有零点,即存在
内有零点,即存在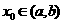 ,使得
,使得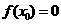 ,这个
,这个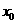 也就是方程
也就是方程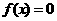 的根。
的根。
但要注意:如果函数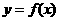 在
在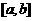 上的图象是连续不断的曲线,且
上的图象是连续不断的曲线,且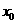 是函数在这个区间上的一个零点,却不一定有
是函数在这个区间上的一个零点,却不一定有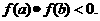
1.函数零点的概念
对于函数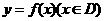 ,我们把使
,我们把使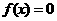 的实数x叫做函数
的实数x叫做函数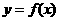 的零点,注意以下几点:
的零点,注意以下几点:
(1)函数的零点是一个实数,当函数的自变量取这个实数时,其函数值等于零。
(2)函数的零点也就是函数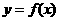 的图象与x轴的交点的横坐标。
的图象与x轴的交点的横坐标。
(3)一般我们只讨论函数的实数零点。
(4)求零点就是求方程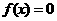 的实数根。
的实数根。
11、已知二次函数f(x)=ax2+bx+c(a,b,c∈R),且同时满足下列条件:①f(-1)=0;②对任意的实数x,都有f(x)-x≥0;③当x∈(0,2)时,有f(x) ≤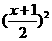 .
.
(Ⅰ)求f(1);
(Ⅱ)求a,b,c的值;
(Ⅲ)当x∈[-1,1]时,函数g(x)=f(x)-mx(m是实数)是单调函数,求m的取值范围..
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com